一、题目
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 ‘Q’ 和 ’.’ 分别代表了皇后和空位。
二、输入
n = 4
三、输出
4 皇后问题的所有解
四、示例
输入:
4
输出:
[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
如下图所示,4 皇后问题存在两个不同的解法。
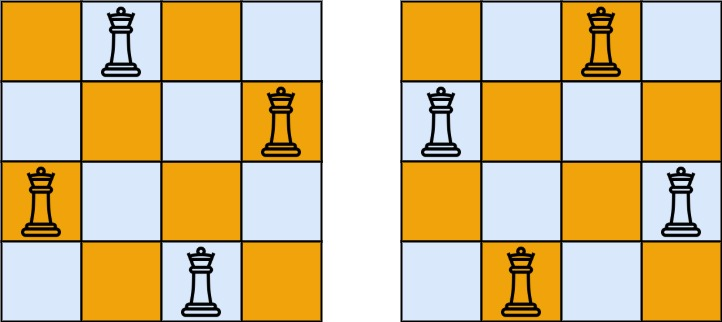
五、题解
- N 皇后问题求解经典算法是回溯算法
- 本文也给出了基于位运算的求解方式,需要掌握位运算的常见操作(比如取最后一位 1,去掉最后一位 1 等)。重点理解递归过程中斜线 pie,na 的移位运算
5.1 Java 实现
- 位运算求解
package org.stone.study.algo.ex202412;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
/**
* N皇后问题,位运算解法
* Q 代表放皇后的位置,.代表空位
* 回溯
*/
public class NQueueProblem {
public static void main(String[] args) {
int n = 8;
// 记录每行放皇后的位置(列号)
int[] queue = new int[n];
Arrays.fill(queue, -1);
List<List<String>> ans = new ArrayList<>();
backtrack(0, n, 0, 0, 0, queue, ans);
// 92
//System.out.println("total:" + ans.size());
for (List<String> board : ans) {
for (String row : board) {
System.out.println(row);
}
System.out.println();
}
}
/**
* 回溯
* @param row 当前行
* @param n 总行数
* @param col 列的限制
* @param pie 撇的限制
* @param na 捺的限制
* @param queue 记录每行放皇后的位置(列号)
* @param ans 最终结果
*/
public static void backtrack(int row, int n, int col, int pie, int na, int[] queue, List<List<String>> ans) {
if (row == n) {
List<String> board = generateBoard(queue, n);
ans.add(board);
return;
}
// 得到当前所有的空位
int availPos = ((1 << n) - 1) & (~(col | pie | na));
// 遍历空位
while (availPos != 0) {
// 取最低位的1
int pos = availPos & (-availPos);
// 将最低位位置1置为0,表示该位置已经放置了皇后
availPos = availPos & (availPos - 1);
// 放置皇后
int column = Integer.bitCount(pos - 1);
queue[row] = column;
// pie往左移,下一行中位置变小,位运算往右移合理一些;na 相反
backtrack(row + 1, n, col | pos, (pie | pos) >> 1, (na | pos) << 1, queue, ans);
// 回溯,将皇后移除
queue[row] = -1;
}
}
private static List<String> generateBoard(int[] queue, int n) {
List<String> board = new ArrayList<>();
for (int i = 0; i < n; i++) {
char[] row = new char[n];
Arrays.fill(row, '.');
row[queue[i]] = 'Q';
board.add(new String(row));
}
return board;
}
}- 回溯算法求解
class Solution {
public List<List<String>> solveNQueens(int n) {
List<List<String>> ans = new ArrayList<>();
// 初始化棋盘,都是.
List<char[]> oneSolution = new ArrayList<>();
for(int i = 0; i < n; i++) {
char[] arr = new char[n];
Arrays.fill(arr, '.');
oneSolution.add(arr);
}
//回溯
backtrack(0, n, oneSolution, ans);
return ans;
}
// 回溯求解。oneSolution 是当前正在尝试的解法
private void backtrack(int curRow, int n, List<char[]> oneSolution, List<List<String>> ans) {
if(curRow == n) {
List<String> l = new ArrayList<>();
for(char[] arr : oneSolution) {
l.add(new String(arr));
}
ans.add(l);
return;
}
char[] arr = oneSolution.get(curRow);
for(int curCol = 0; curCol < n; curCol++) {
arr[curCol] = 'Q';
if(valid(curRow, curCol, n, oneSolution)) {
backtrack(curRow + 1, n, oneSolution, ans);
}
arr[curCol] = '.';
}
}
// row,col 放皇后是否合法
private boolean valid(int row, int col, int n, List<char[]> oneSolution) {
// 列规则是否通过
for(int i = 0; i < row; i++) {
if(oneSolution.get(i)[col] == 'Q') {
return false;
}
}
// 正斜线规则是否通过
int j = col;
for(int i = row - 1; i >= 0; i--) {
++j;
if(j < n && oneSolution.get(i)[j] == 'Q') {
return false;
}
}
// 反斜线规则是否通过
j = col;
for(int i = row - 1; i >= 0; i--) {
--j;
if(j >= 0 && oneSolution.get(i)[j] == 'Q') {
return false;
}
}
return true;
}
}5.2 Python实现
# 打印一种解的棋盘
def generateBoard(queue, n):
board = []
for res in queue:
row = '.' * n
for i in range(n):
if ((res >> i) & 1) == 1:
row = row[:i] + 'Q' + row[i + 1:]
board.append(row)
return board
# 回溯算法求解
def backtrack(row, n, col, pie, na, queue, res):
# 递归终止条件
if row == n:
# 一种解法
res.append(generateBoard(queue, n))
return
# 得到当前所有的空位
bits = (~(col | pie | na)) & ((1 << n) - 1)
while bits:
# 取最低位的1
p = bits & -bits
# 去掉最低位的1
bits = bits & (bits - 1)
# 把皇后放到空位上
queue.append(p)
# DFS 到下一行
backtrack(row + 1, n, col | p, (pie | p) >> 1, (na | p) << 1, queue, res)
# 清理当前层
queue.pop()
if __name__ == '__main__':
n = 8
# 所有解法的列表
res = []
# 一种解法
queue = []
# 求解 N 皇后问题的解,解放到一个列表中,Q 代表皇后位置,. 代表空格
backtrack(0, n, 0, 0, 0, queue, res)
print(len(res))