动态规划之博弈问题

通知:数据结构精品课 和 递归算法专题课 限时附赠网站会员,全新纸质书《labuladong 的算法笔记》 出版,签名版限时半价!另外,建议你在我的 网站 学习文章,体验更好。
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
| LeetCode | 力扣 | 难度 |
|---|---|---|
| 486. Predict the Winner | 486. 预测赢家 | 🟠 |
| 877. Stone Game | 877. 石子游戏 | 🟠 |
-----------
上一篇文章 几道智力题 中讨论到一个有趣的「石头游戏」,通过题目的限制条件,这个游戏是先手必胜的。但是智力题终究是智力题,真正的算法问题肯定不会是投机取巧能搞定的。所以,本文就借石头游戏来讲讲「假设两个人都足够聪明,最后谁会获胜」这一类问题该如何用动态规划算法解决。
博弈类问题的套路都差不多,下文参考 这个 YouTube 视频 的思路讲解,其核心思路是在二维 dp 的基础上使用元组分别存储两个人的博弈结果。掌握了这个技巧以后,别人再问你什么俩海盗分宝石,俩人拿硬币的问题,你就告诉别人:我懒得想,直接给你写个算法算一下得了。
我们把力扣第 877 题「石头游戏」改的更具有一般性:
你和你的朋友面前有一排石头堆,用一个数组 piles 表示,piles[i] 表示第 i 堆石子有多少个。你们轮流拿石头,一次拿一堆,但是只能拿走最左边或者最右边的石头堆。所有石头被拿完后,谁拥有的石头多,谁获胜。
石头的堆数可以是任意正整数,石头的总数也可以是任意正整数,这样就能打破先手必胜的局面了。比如有三堆石头 piles = [1, 100, 3],先手不管拿 1 还是 3,能够决定胜负的 100 都会被后手拿走,后手会获胜。
假设两人都很聪明,请你写一个 stoneGame 函数,返回先手和后手的最后得分(石头总数)之差。比如上面那个例子,先手能获得 4 分,后手会获得 100 分,你的算法应该返回 -96。
这样推广之后就变成了一道难度比较高的动态规划问题了,力扣第 486 题「预测赢家」就是一道类似的问题:
函数签名如下:
boolean PredictTheWinner(int[] nums);那么如果有了一个计算先手和后手分差的 stoneGame 函数,这道题的解法就直接出来了:
public boolean PredictTheWinner(int[] nums) {
// 先手的分数大于等于后手,则能赢
return stoneGame(nums) >= 0;
}这个 stoneGame 函数怎么写呢?博弈问题的难点在于,两个人要轮流进行选择,而且都贼精明,应该如何编程表示这个过程呢?其实不难,还是按照 动态规划核心框架 中强调多次的套路,首先明确 dp 数组的含义,然后只要找到「状态」和「选择」,一切就水到渠成了。
一、定义 dp 数组的含义
定义 dp 数组的含义是很有技术含量的,同一问题可能有多种定义方法,不同的定义会引出不同的状态转移方程,不过只要逻辑没有问题,最终都能得到相同的答案。
我建议不要迷恋那些看起来很牛逼,代码很短小的解法思路,最好是稳一点,采取可解释性最好,最容易推广的解法思路。本文就给出一种博弈问题的通用设计框架。
介绍 dp 数组的含义之前,我们先看一下 dp 数组最终的样子:
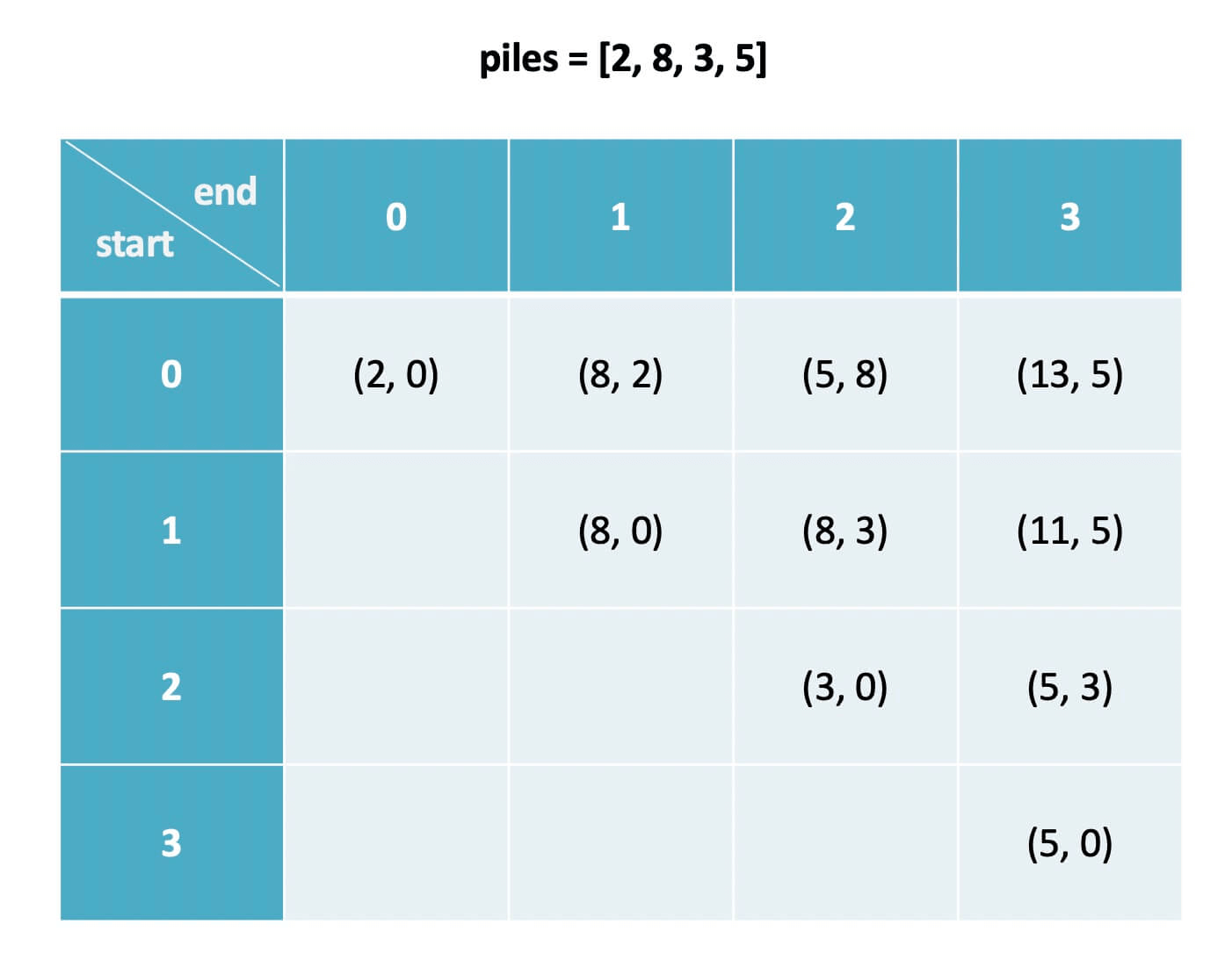
下文讲解时,认为元组是包含 first 和 second 属性的一个类,而且为了节省篇幅,将这两个属性简写为 fir 和 sec。比如按上图的数据,我们说 dp[1][3].fir = 11,dp[0][1].sec = 2。
先回答几个读者可能提出的问题:
这个二维 dp table 中存储的是元组,怎么编程表示呢?这个 dp table 有一半根本没用上,怎么优化?很简单,都不要管,先把解题的思路想明白了再谈也不迟。
以下是对 dp 数组含义的解释:
dp[i][j].fir = x 表示,对于 piles[i...j] 这部分石头堆,先手能获得的最高分数为 x。
dp[i][j].sec = y 表示,对于 piles[i...j] 这部分石头堆,后手能获得的最高分数为 y。
举例理解一下,假设 piles = [2, 8, 3, 5],索引从 0 开始,那么:
dp[0][1].fir = 8 意味着:面对石头堆 [2, 8],先手最多能够获得 8 分;dp[1][3].sec = 5 意味着:面对石头堆 [8, 3, 5],后手最多能够获得 5 分。
我们想求的答案是先手和后手最终分数之差,按照这个定义也就是 dp[0][n-1].fir - dp[0][n-1].sec,即面对整个 piles,先手的最优得分和后手的最优得分之差。
二、状态转移方程
写状态转移方程很简单,首先要找到所有「状态」和每个状态可以做的「选择」,然后择优。
根据前面对 dp 数组的定义,状态显然有三个:开始的索引 i,结束的索引 j,当前轮到的人。
dp[i][j][fir or sec]
其中:
0 <= i < piles.length
i <= j < piles.length对于这个问题的每个状态,可以做的选择有两个:选择最左边的那堆石头,或者选择最右边的那堆石头。 我们可以这样穷举所有状态:
n = piles.length
for 0 <= i < n:
for j <= i < n:
for who in {fir, sec}:
dp[i][j][who] = max(left, right)上面的伪码是动态规划的一个大致的框架,这道题的难点在于,两人足够聪明,而且是交替进行选择的,也就是说先手的选择会对后手有影响,这怎么表达出来呢?
根据我们对 dp 数组的定义,很容易解决这个难点,写出状态转移方程:
dp[i][j].fir = max(piles[i] + dp[i+1][j].sec, piles[j] + dp[i][j-1].sec)
dp[i][j].fir = max( 选择最左边的石头堆 , 选择最右边的石头堆 )
# 解释:我作为先手,面对 piles[i...j] 时,有两种选择:
# 要么我选择最左边的那一堆石头 piles[i],局面变成了 piles[i+1...j],
# 然后轮到对方选了,我变成了后手,此时我作为后手的最优得分是 dp[i+1][j].sec
# 要么我选择最右边的那一堆石头 piles[j],局面变成了 piles[i...j-1]
# 然后轮到对方选了,我变成了后手,此时我作为后手的最优得分是 dp[i][j-1].sec
if 先手选择左边:
dp[i][j].sec = dp[i+1][j].fir
if 先手选择右边:
dp[i][j].sec = dp[i][j-1].fir
# 解释:我作为后手,要等先手先选择,有两种情况:
# 如果先手选择了最左边那堆,给我剩下了 piles[i+1...j]
# 此时轮到我,我变成了先手,此时的最优得分是 dp[i+1][j].fir
# 如果先手选择了最右边那堆,给我剩下了 piles[i...j-1]
# 此时轮到我,我变成了先手,此时的最优得分是 dp[i][j-1].fir根据 dp 数组的定义,我们也可以找出 base case,也就是最简单的情况:
dp[i][j].fir = piles[i]
dp[i][j].sec = 0
其中 0 <= i == j < n
# 解释:i 和 j 相等就是说面前只有一堆石头 piles[i]
# 那么显然先手的得分为 piles[i]
# 后手没有石头拿了,得分为 0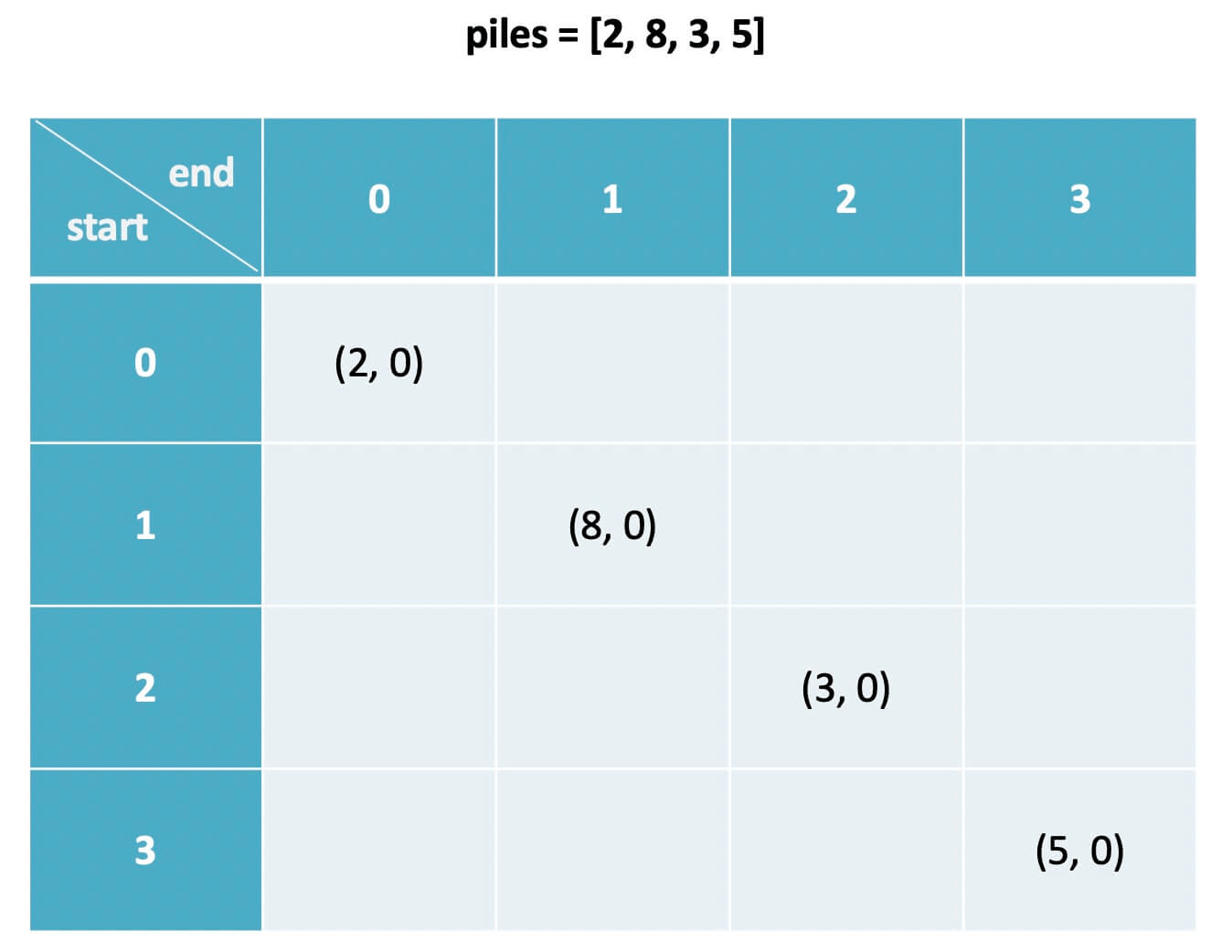
这里需要注意一点,我们发现 base case 是斜着的,而且我们推算 dp[i][j] 时需要用到 dp[i+1][j] 和 dp[i][j-1]:
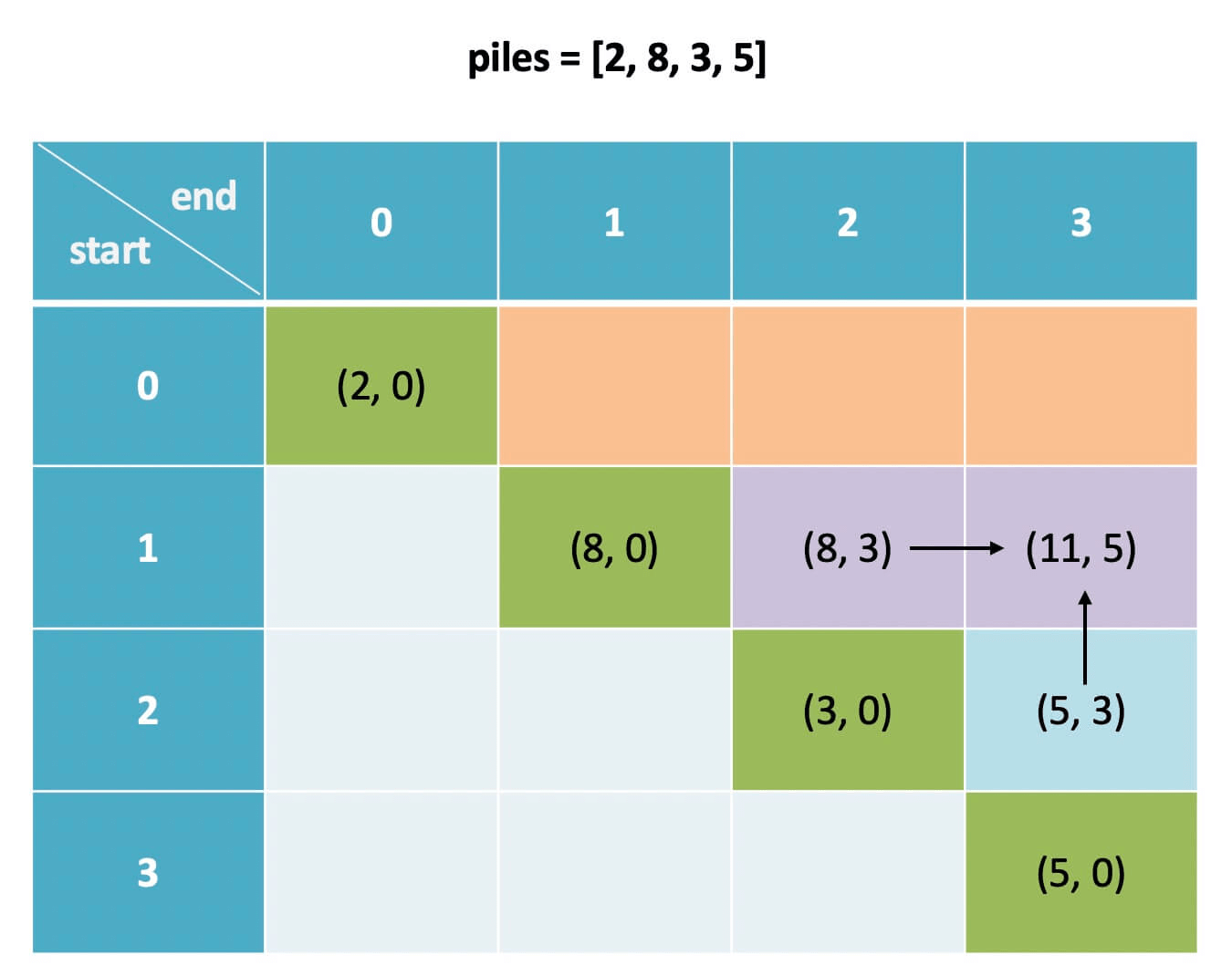
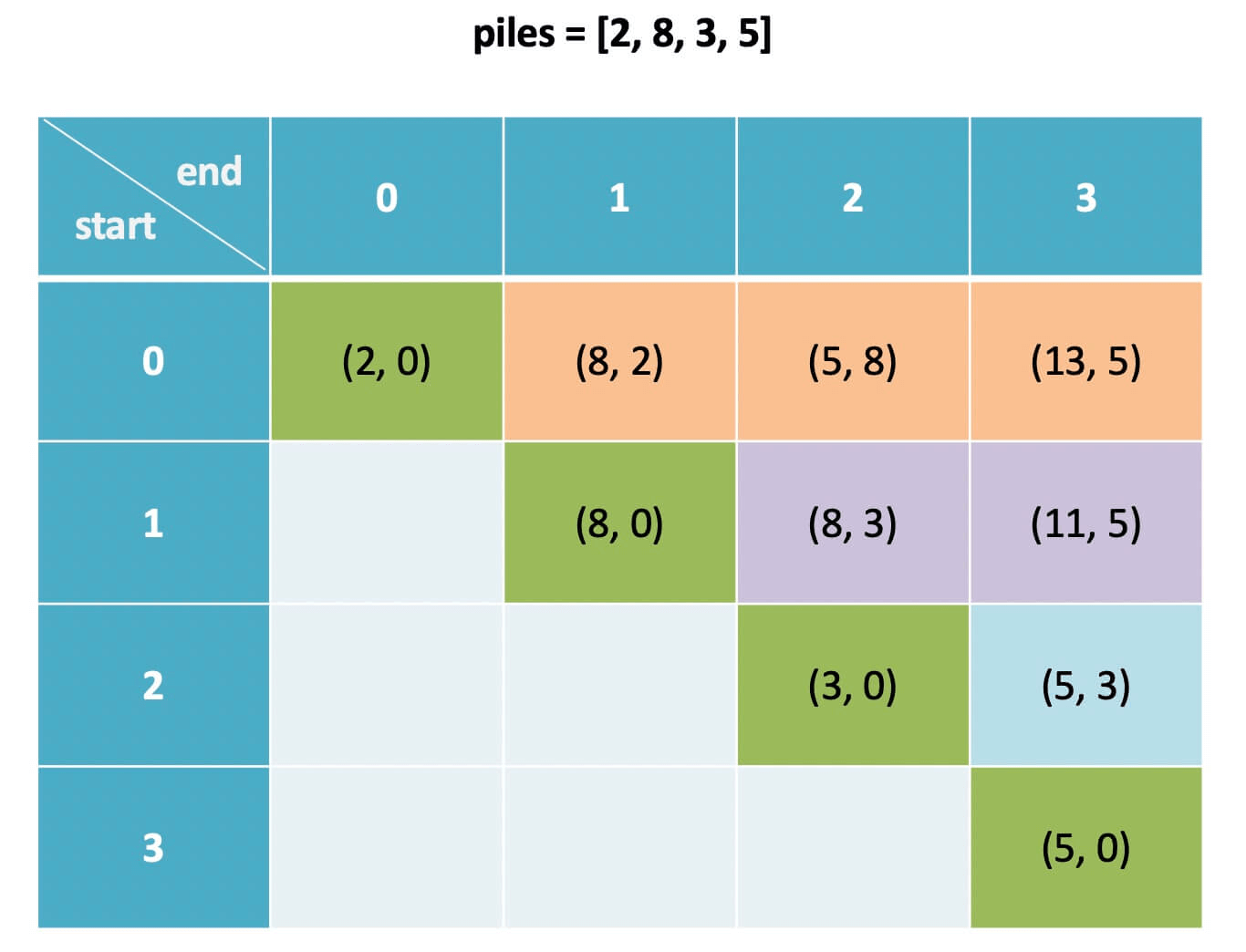
根据前文 动态规划答疑篇 判断 dp 数组遍历方向的原则,算法应该倒着遍历 dp 数组:
for (int i = n - 2; i >= 0; i--) {
for (int j = i + 1; j < n; j++) {
dp[i][j] = ...
}
}
三、代码实现
如何实现这个 fir 和 sec 元组呢,你可以用 python,自带元组类型;或者使用 C++ 的 pair 容器;或者用一个三维数组 dp[n][n][2],最后一个维度就相当于元组;或者我们自己写一个 Pair 类:
class Pair {
int fir, sec;
Pair(int fir, int sec) {
this.fir = fir;
this.sec = sec;
}
}然后直接把我们的状态转移方程翻译成代码即可,注意我们要倒着遍历数组:
/* 返回游戏最后先手和后手的得分之差 */
int stoneGame(int[] piles) {
int n = piles.length;
// 初始化 dp 数组
Pair[][] dp = new Pair[n][n];
for (int i = 0; i < n; i++)
for (int j = i; j < n; j++)
dp[i][j] = new Pair(0, 0);
// 填入 base case
for (int i = 0; i < n; i++) {
dp[i][i].fir = piles[i];
dp[i][i].sec = 0;
}
// 倒着遍历数组
for (int i = n - 2; i >= 0; i--) {
for (int j = i + 1; j < n; j++) {
// 先手选择最左边或最右边的分数
int left = piles[i] + dp[i+1][j].sec;
int right = piles[j] + dp[i][j-1].sec;
// 套用状态转移方程
// 先手肯定会选择更大的结果,后手的选择随之改变
if (left > right) {
dp[i][j].fir = left;
dp[i][j].sec = dp[i+1][j].fir;
} else {
dp[i][j].fir = right;
dp[i][j].sec = dp[i][j-1].fir;
}
}
}
Pair res = dp[0][n-1];
return res.fir - res.sec;
}动态规划解法,如果没有状态转移方程指导,绝对是一头雾水,但是根据前面的详细解释,读者应该可以清晰理解这一大段代码的含义。
而且,注意到计算 dp[i][j] 只依赖其左边和下边的元素,所以说肯定有优化空间,转换成一维 dp,想象一下把二维平面压扁,也就是投影到一维。但是,一维 dp 比较复杂,可解释性比较差,大家就不必浪费这个时间去理解了。
四、最后总结
本文给出了解决博弈问题的动态规划解法。博弈问题的前提一般都是在两个聪明人之间进行,编程描述这种游戏的一般方法是二维 dp 数组,数组中通过元组分别表示两人的最优决策。
之所以这样设计,是因为先手在做出选择之后,就成了后手,后手在对方做完选择后,就变成了先手。这种角色转换使得我们可以重用之前的结果,典型的动态规划标志。
读到这里的朋友应该能理解算法解决博弈问题的套路了。学习算法,一定要注重算法的模板框架,而不是一些看起来牛逼的思路,也不要奢求上来就写一个最优的解法。不要舍不得多用空间,不要过早尝试优化,不要惧怕多维数组。dp 数组就是存储信息避免重复计算的,随便用,直到咱满意为止。
引用本文的文章
_____________
《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复「全家桶」可下载配套 PDF 和刷题全家桶:

====其他语言代码====
python
由SCUHZS提供
这里采取的是三维的做法
class Solution:
def stoneGame(self, piles: List[int]) -> bool:
n = len(piles)
# 初始化一个n*n的矩阵 dp数组
dp = [[None] * n for i in range(0, n)]
# 在三角区域填充
for i in range(n):
for j in range(i, n):
dp[i][j] = [0, 0]
# 填入base case
for i in range(0, n):
dp[i][i][0] = piles[i]
dp[i][i][1] = 0
# 斜着遍历数组
for l in range(2, n + 1):
for i in range(0, n-l+1):
j = l + i - 1
# 先手选择最左边或最右边的分数
left = piles[i] + dp[i + 1][j][1]
right = piles[j] + dp[i][j - 1][1]
# 套用状态转移方程
if left > right:
dp[i][j][0] = left
dp[i][j][1] = dp[i + 1][j][0]
else:
dp[i][j][0] = right
dp[i][j][1] = dp[i][j - 1][0]
res = dp[0][n - 1]
return res[0] - res[1] > 0
压缩成一维数组,以减小空间复杂度,做法如下。
class Solution:
def stoneGame(self, piles: List[int]) -> bool:
dp = piles.copy()
for i in range(len(piles) - 1, -1, -1): # 从下往上遍历
for j in range(i, len(piles)): # 从前往后遍历
dp[j] = max(piles[i] - dp[j], piles[j] - dp[j - 1]) # 计算之后覆盖一维数组的对应位置
return dp[len(piles) - 1] > 0
C++ 版本
由 TCeason 提供
这里采用 hash map 来解决问题
class Solution {
public:
unordered_map<int, int> memo;
int dfs(vector<int> &piles, int index) {
// 从两边向中间获取
// index 值为 1/2 piles.size() 时可以停止算法
if (index == piles.size() / 2)
return 0;
// 减少计算,快速返回已有结果
if (memo.count(index))
return memo[index];
// 防止第一次取最右时越界
int n = piles.size() - 1;
// 先手选择最左边或最右边后的分数
int l = piles[index] + dfs(piles, index + 1);
int r = piles[n - index] + dfs(piles, index + 1);
// 返回先手左或右边的最高分
return memo[index] = max(l, r);
}
bool stoneGame(vector<int>& piles) {
// 最佳发挥时:
// 先手得分 * 2 > 总大小 则先手者胜利
return dfs(piles, 0) * 2 > accumulate(begin(piles), end(piles), 0);
}
};
javascript
由SCUHZS提供
1、暴力递归解
/**
* 返回[i,j]上先手所能取得的最优决策的值
* @param piles
* @param i
* @param j
* @return {number|*}
*/
var f=function(piles,i,j) {
if(i===j){ //如果i===j,只有一个元素,那么先手只能选它
return piles[i]
}
//否则 有2种情况:
//1 先选i,之后在[i+1,j]上后手进行最优选择
//2 先选j,之后在[i,j-1]上后手进行最优选择
return Math.max(piles[i]+s(i+1,j),piles[j]+s(i,j-1))
}
/**
*返回[i,j]上后手所能取得的最优决策的值
* @param piles
* @param i
* @param j
* @return {number}
*/
var s=function(piles,i,j) {
if(i===j){ //如果i===j,只有一个元素,那么后手没有选,只能为0
return 0
}
//对于这种双方都是绝顶聪明的人,数据一开始对于双方都是可见的,那么数据一确定,先后手一确定,那么结果就已经确定了
//先手选的人会把最优解选了,那么剩给后手的只有最差的情况
//所以后手的人虽然能从剩下的之中进行最优决策,但结果确是命中注定的了,只能是最差的
//所以返回[i+1,j] [i,j-1]上进行最优选择的最小值
//这也说明了先手的人在大概率下会赢得游戏(在某些情况下先手必赢,比如本题的情况:具体分析看官方解析)
return Math.min(f(i+1,j),f(i,j-1))
}
/**
*
* @param piles
* @return {boolean}
*/
var stoneGame = function(piles) {
return f(0,piles.length-1)>s(0,piles.length-1) //亚历克斯先选和李后选得到的最大值做比较
};2、动态规划dp做法
这里采取的是三维的做法
var stoneGame = function (piles) {
let n = piles.length;
// 初始化一个n*n的矩阵 dp数组
let dp = []
for (let i = 0; i < n; i++) {
dp[i] = []
}
// 在三角区域填充
for (let i = 0; i < n; i++) {
for (let j = i; j < n; j++) {
dp[i][j] = [0, 0]
}
}
// 填入base case
for (let i = 0; i < n; i++) {
dp[i][i][0] = piles[i];
dp[i][i][1] = 0;
}
// 斜着遍历数组
for (let l = 2; l <= n; l++) {
for (let i = 0; i <= n - 1; i++) {
let j = l + i - 1;
// 先手选择最左边或最右边的分数
let left = piles[i] + dp[i + 1][j][1];
let right = piles[j] + dp[i][j - 1][1];
// 套用状态转移方程
if (left > right) {
dp[i][j][0] = left;
dp[i][j][1] = dp[i + 1][j][0];
} else {
dp[i][j][0] = right;
dp[i][j][1] = dp[i][j - 1][0];
}
}
}
let res = dp[0][n - 1];
return res[0] - res[1]
};


