参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
1382.将二叉搜索树变平衡
给你一棵二叉搜索树,请你返回一棵 平衡后 的二叉搜索树,新生成的树应该与原来的树有着相同的节点值。
如果一棵二叉搜索树中,每个节点的两棵子树高度差不超过 1 ,我们就称这棵二叉搜索树是 平衡的 。
如果有多种构造方法,请你返回任意一种。
示例:
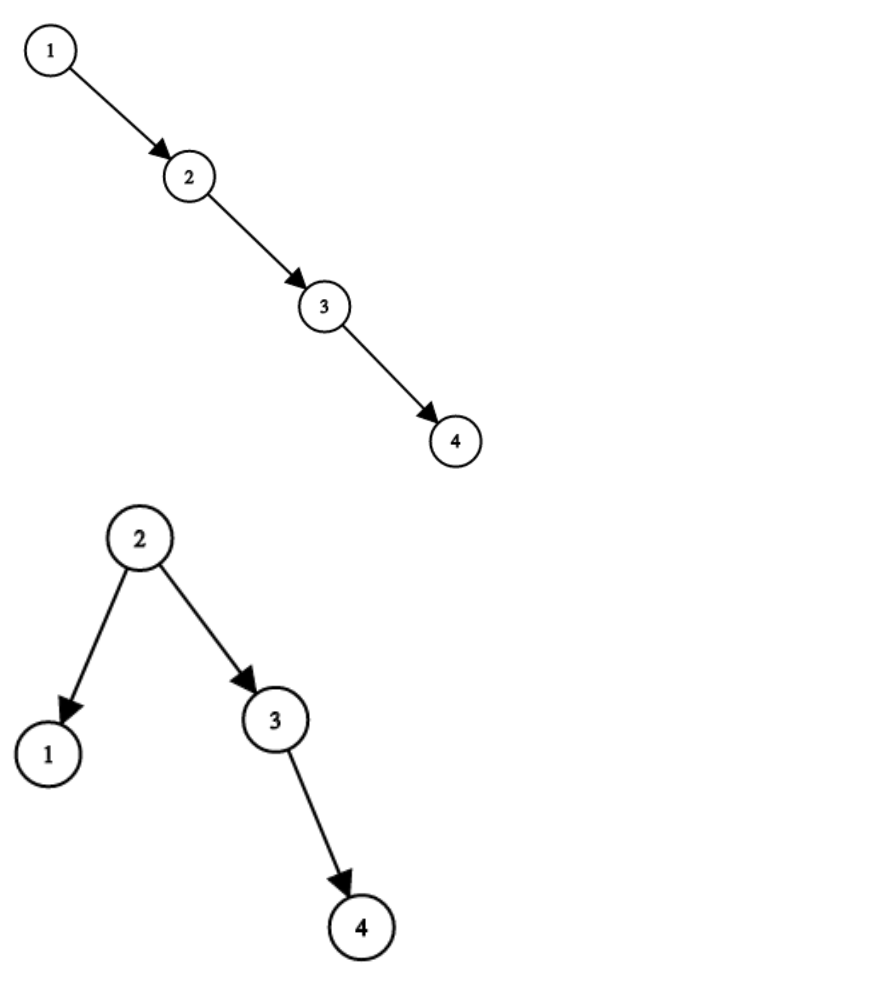
- 输入:root = [1,null,2,null,3,null,4,null,null]
- 输出:[2,1,3,null,null,null,4]
- 解释:这不是唯一的正确答案,[3,1,4,null,2,null,null] 也是一个可行的构造方案。
提示:
- 树节点的数目在 1 到 10^4 之间。
- 树节点的值互不相同,且在 1 到 10^5 之间。
思路
这道题目,可以中序遍历把二叉树转变为有序数组,然后在根据有序数组构造平衡二叉搜索树。
建议做这道题之前,先看如下两篇题解:
- 98.验证二叉搜索树 学习二叉搜索树的特性
- 108.将有序数组转换为二叉搜索树 学习如何通过有序数组构造二叉搜索树
这两道题目做过之后,本题分分钟就可以做出来了。
代码如下:
class Solution {
private:
vector<int> vec;
// 有序树转成有序数组
void traversal(TreeNode* cur) {
if (cur == nullptr) {
return;
}
traversal(cur->left);
vec.push_back(cur->val);
traversal(cur->right);
}
// 有序数组转平衡二叉树
TreeNode* getTree(vector<int>& nums, int left, int right) {
if (left > right) return nullptr;
int mid = left + ((right - left) / 2);
TreeNode* root = new TreeNode(nums[mid]);
root->left = getTree(nums, left, mid - 1);
root->right = getTree(nums, mid + 1, right);
return root;
}
public:
TreeNode* balanceBST(TreeNode* root) {
traversal(root);
return getTree(vec, 0, vec.size() - 1);
}
};其他语言版本
Java:
class Solution {
ArrayList <Integer> res = new ArrayList<Integer>();
// 有序树转成有序数组
private void travesal(TreeNode cur) {
if (cur == null) return;
travesal(cur.left);
res.add(cur.val);
travesal(cur.right);
}
// 有序数组转成平衡二叉树
private TreeNode getTree(ArrayList <Integer> nums, int left, int right) {
if (left > right) return null;
int mid = left + (right - left) / 2;
TreeNode root = new TreeNode(nums.get(mid));
root.left = getTree(nums, left, mid - 1);
root.right = getTree(nums, mid + 1, right);
return root;
}
public TreeNode balanceBST(TreeNode root) {
travesal(root);
return getTree(res, 0, res.size() - 1);
}
}Python:
class Solution:
def balanceBST(self, root: TreeNode) -> TreeNode:
res = []
# 有序树转成有序数组
def traversal(cur: TreeNode):
if not cur: return
traversal(cur.left)
res.append(cur.val)
traversal(cur.right)
# 有序数组转成平衡二叉树
def getTree(nums: List, left, right):
if left > right: return
mid = left + (right -left) // 2
root = TreeNode(nums[mid])
root.left = getTree(nums, left, mid - 1)
root.right = getTree(nums, mid + 1, right)
return root
traversal(root)
return getTree(res, 0, len(res) - 1)Go:
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func balanceBST(root *TreeNode) *TreeNode {
// 二叉搜索树中序遍历得到有序数组
nums := []int{}
// 中序递归遍历二叉树
var travel func(node *TreeNode)
travel = func(node *TreeNode) {
if node == nil {
return
}
travel(node.Left)
nums = append(nums, node.Val)
travel(node.Right)
}
// 二分法保证左右子树高度差不超过一(题目要求返回的仍是二叉搜索树)
var buildTree func(nums []int, left, right int) *TreeNode
buildTree = func(nums []int, left, right int) *TreeNode {
if left > right {
return nil
}
mid := left + (right-left) >> 1
root := &TreeNode{Val: nums[mid]}
root.Left = buildTree(nums, left, mid-1)
root.Right = buildTree(nums, mid+1, right)
return root
}
travel(root)
return buildTree(nums, 0, len(nums)-1)
}
JavaScript:
var balanceBST = function(root) {
const res = [];
// 中序遍历转成有序数组
const travesal = cur => {
if(!cur) return;
travesal(cur.left);
res.push(cur.val);
travesal(cur.right);
}
// 有序数组转成平衡二叉树
const getTree = (nums, left, right) => {
if(left > right) return null;
let mid = left + ((right - left) >> 1);
let root = new TreeNode(nums[mid]);// 中心位置作为当前节点的值
root.left = getTree(nums, left, mid - 1);// 递归地将区间[left,mid−1] 作为当前节点的左子树
root.right = getTree(nums, mid + 1, right);// 递归地将区间[mid+1,right] 作为当前节点的左子树
return root;
}
travesal(root);
return getTree(res, 0, res.length - 1);
};TypeScript:
function balanceBST(root: TreeNode | null): TreeNode | null {
const inorderArr: number[] = [];
inorderTraverse(root, inorderArr);
return buildTree(inorderArr, 0, inorderArr.length - 1);
};
function inorderTraverse(node: TreeNode | null, arr: number[]): void {
if (node === null) return;
inorderTraverse(node.left, arr);
arr.push(node.val);
inorderTraverse(node.right, arr);
}
function buildTree(arr: number[], left: number, right: number): TreeNode | null {
if (left > right) return null;
const mid = (left + right) >> 1;
const resNode: TreeNode = new TreeNode(arr[mid]);
resNode.left = buildTree(arr, left, mid - 1);
resNode.right = buildTree(arr, mid + 1, right);
return resNode;
}
