众里寻他千百度:找网红算法

通知:数据结构精品课 和 递归算法专题课 限时附赠网站会员,全新纸质书《labuladong 的算法笔记》 出版,签名版限时半价!另外,建议你在我的 网站 学习文章,体验更好。
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
| LeetCode | 力扣 | 难度 |
|---|---|---|
| 277. Find the Celebrity🔒 | 277. 搜寻名人🔒 | 🟠 |
-----------
今天来讨论经典的「名流问题」:
给你 n 个人的社交关系(你知道任意两个人之间是否认识),然后请你找出这些人中的「名人」。
所谓「名人」有两个条件:
1、所有其他人都认识「名人」。
2、「名人」不认识任何其他人。
这是一个图相关的算法问题,社交关系嘛,本质上就可以抽象成一幅图。
如果把每个人看做图中的节点,「认识」这种关系看做是节点之间的有向边,那么名人就是这幅图中一个特殊的节点:
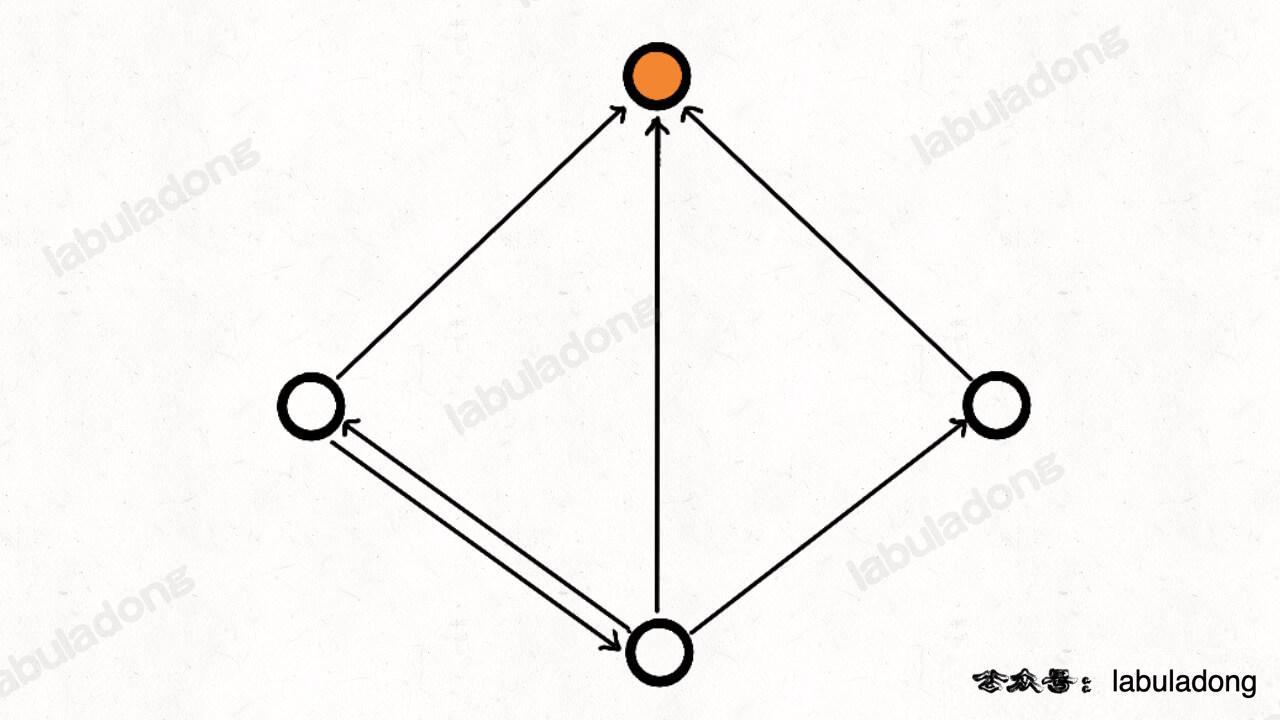
这个节点没有一条指向其他节点的有向边;且其他所有节点都有一条指向这个节点的有向边。
或者说的专业一点,名人节点的出度为 0,入度为 n - 1。
那么,这 n 个人的社交关系是如何表示的呢?
前文 图论算法基础 说过,图有两种存储形式,一种是邻接表,一种是邻接矩阵,邻接表的主要优势是节约存储空间;邻接矩阵的主要优势是可以迅速判断两个节点是否相邻。
对于名人问题,显然会经常需要判断两个人之间是否认识,也就是两个节点是否相邻,所以我们可以用邻接矩阵来表示人和人之间的社交关系。
那么,把名流问题描述成算法的形式就是这样的:
给你输入一个大小为 n x n 的二维数组(邻接矩阵) graph 表示一幅有 n 个节点的图,每个人都是图中的一个节点,编号为 0 到 n - 1。
如果 graph[i][j] == 1 代表第 i 个人认识第 j 个人,如果 graph[i][j] == 0 代表第 i 个人不认识第 j 个人。
有了这幅图表示人与人之间的关系,请你计算,这 n 个人中,是否存在「名人」?
如果存在,算法返回这个名人的编号,如果不存在,算法返回 -1。
函数签名如下:
int findCelebrity(int[][] graph);比如输入的邻接矩阵长这样:
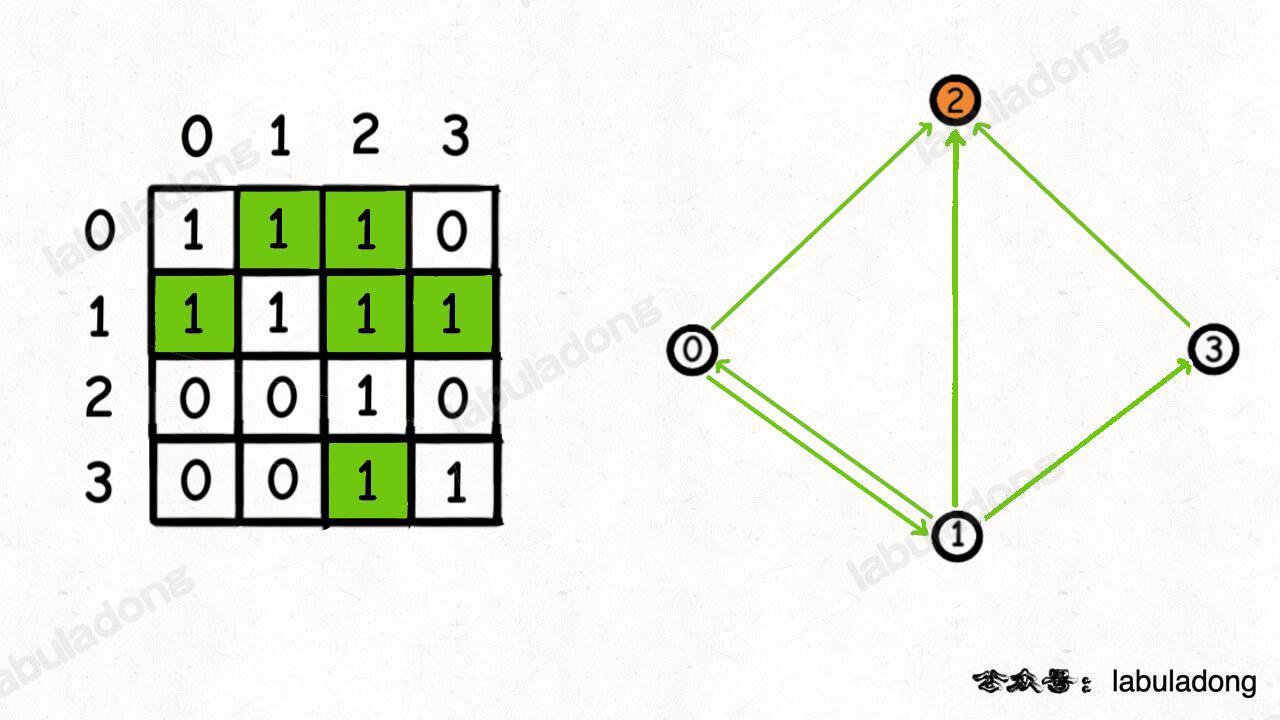
那么算法应该返回 2。
力扣第 277 题「搜寻名人」就是这个经典问题,不过并不是直接把邻接矩阵传给你,而是只告诉你总人数 n,同时提供一个 API knows 来查询人和人之间的社交关系:
// 可以直接调用,能够返回 i 是否认识 j
boolean knows(int i, int j);
// 请你实现:返回「名人」的编号
int findCelebrity(int n) {
// todo
}很明显,knows API 本质上还是在访问邻接矩阵。为了简单起见,我们后面就按力扣的题目形式来探讨一下这个经典问题。
暴力解法
我们拍拍脑袋就能写出一个简单粗暴的算法:
int findCelebrity(int n) {
for (int cand = 0; cand < n; cand++) {
int other;
for (other = 0; other < n; other++) {
if (cand == other) continue;
// 保证其他人都认识 cand,且 cand 不认识任何其他人
// 否则 cand 就不可能是名人
if (knows(cand, other) || !knows(other, cand)) {
break;
}
}
if (other == n) {
// 找到名人
return cand;
}
}
// 没有一个人符合名人特性
return -1;
}cand 是候选人(candidate)的缩写,我们的暴力算法就是从头开始穷举,把每个人都视为候选人,判断是否符合「名人」的条件。
刚才也说了,knows 函数底层就是在访问一个二维的邻接矩阵,一次调用的时间复杂度是 O(1),所以这个暴力解法整体的最坏时间复杂度是 O(N^2)。
那么,是否有其他高明的办法来优化时间复杂度呢?其实是有优化空间的,你想想,我们现在最耗时的地方在哪里?
对于每一个候选人 cand,我们都要用一个内层 for 循环去判断这个 cand 到底符不符合「名人」的条件。
这个内层 for 循环看起来就蠢,虽然判断一个人「是名人」必须用一个 for 循环,但判断一个人「不是名人」就不用这么麻烦了。
因为「名人」的定义保证了「名人」的唯一性,所以我们可以利用排除法,先排除那些显然不是「名人」的人,从而避免 for 循环的嵌套,降低时间复杂度。
优化解法
我再重复一遍所谓「名人」的定义:
1、所有其他人都认识名人。
2、名人不认识任何其他人。
这个定义就很有意思,它保证了人群中最多有一个名人。
这很好理解,如果有两个人同时是名人,那么这两条定义就自相矛盾了。
换句话说,只要观察任意两个候选人的关系,我一定能确定其中的一个人不是名人,把他排除。
至于另一个候选人是不是名人,只看两个人的关系肯定是不能确定的,但这不重要,重要的是排除掉一个必然不是名人的候选人,缩小了包围圈。
这是优化的核心,也是比较难理解的,所以我们先来说说为什么观察任意两个候选人的关系,就能排除掉一个。
你想想,两个人之间的关系可能是什么样的?
无非就是四种:你认识我我不认识你,我认识你你不认识我,咱俩互相认识,咱两互相不认识。
如果把人比作节点,红色的有向边表示不认识,绿色的有向边表示认识,那么两个人的关系无非是如下四种情况:
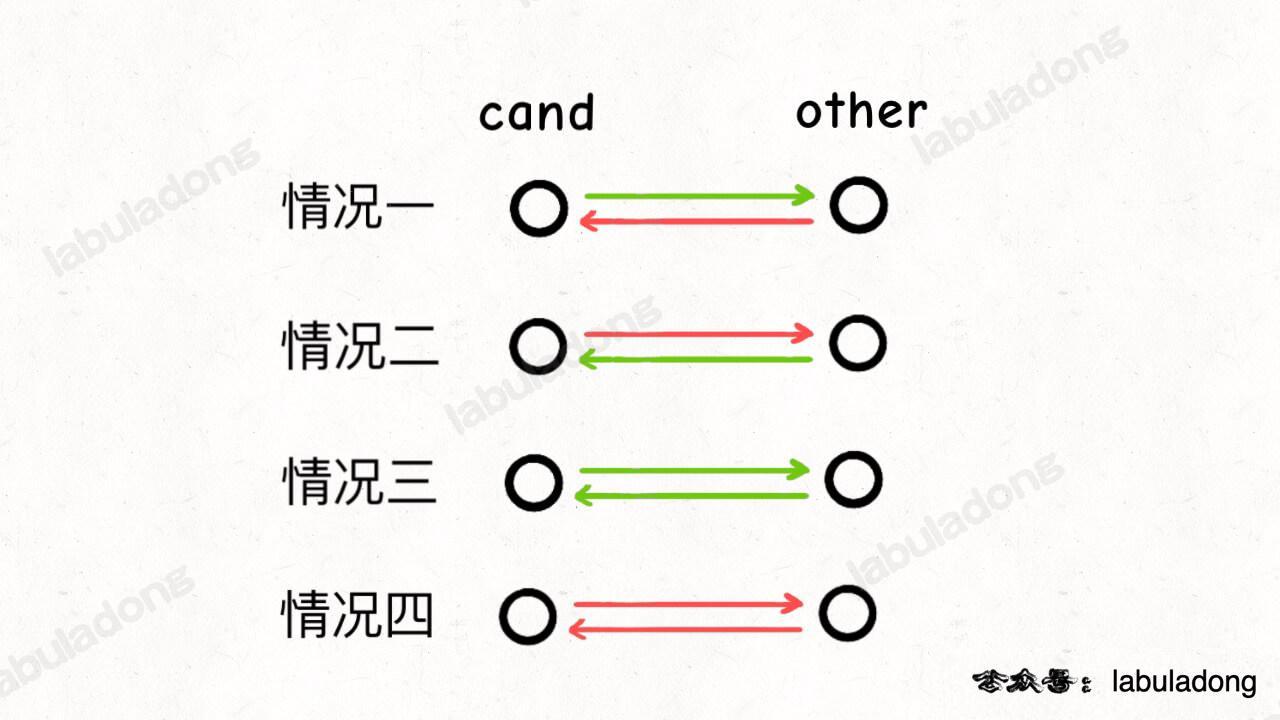
不妨认为这两个人的编号分别是 cand 和 other,然后我们逐一分析每种情况,看看怎么排除掉一个人。
对于情况一,cand 认识 other,所以 cand 肯定不是名人,排除。因为名人不可能认识别人。
对于情况二,other 认识 cand,所以 other 肯定不是名人,排除。
对于情况三,他俩互相认识,肯定都不是名人,可以随便排除一个。
对于情况四,他俩互不认识,肯定都不是名人,可以随便排除一个。因为名人应该被所有其他人认识。
综上,只要观察任意两个之间的关系,就至少能确定一个人不是名人,上述情况判断可以用如下代码表示:
if (knows(cand, other) || !knows(other, cand)) {
// cand 不可能是名人
} else {
// other 不可能是名人
}如果能够理解这一个特点,那么写出优化解法就简单了。
我们可以不断从候选人中选两个出来,然后排除掉一个,直到最后只剩下一个候选人,这时候再使用一个 for 循环判断这个候选人是否是货真价实的「名人」。
这个思路的完整代码如下:
int findCelebrity(int n) {
if (n == 1) return 0;
// 将所有候选人装进队列
LinkedList<Integer> q = new LinkedList<>();
for (int i = 0; i < n; i++) {
q.addLast(i);
}
// 一直排除,直到只剩下一个候选人停止循环
while (q.size() >= 2) {
// 每次取出两个候选人,排除一个
int cand = q.removeFirst();
int other = q.removeFirst();
if (knows(cand, other) || !knows(other, cand)) {
// cand 不可能是名人,排除,让 other 归队
q.addFirst(other);
} else {
// other 不可能是名人,排除,让 cand 归队
q.addFirst(cand);
}
}
// 现在排除得只剩一个候选人,判断他是否真的是名人
int cand = q.removeFirst();
for (int other = 0; other < n; other++) {
if (other == cand) {
continue;
}
// 保证其他人都认识 cand,且 cand 不认识任何其他人
if (!knows(other, cand) || knows(cand, other)) {
return -1;
}
}
// cand 是名人
return cand;
}这个算法避免了嵌套 for 循环,时间复杂度降为 O(N) 了,不过引入了一个队列来存储候选人集合,使用了 O(N) 的空间复杂度。
note:
LinkedList的作用只是充当一个容器把候选人装起来,每次找出两个进行比较和淘汰,但至于具体找出哪两个,都是无所谓的,也就是说候选人归队的顺序无所谓,我们用的是addFirst只是方便后续的优化,你完全可以用addLast,结果都是一样的。
是否可以进一步优化,把空间复杂度也优化掉?
最终解法
如果你能够理解上面的优化解法,其实可以不需要额外的空间解决这个问题,代码如下:
int findCelebrity(int n) {
// 先假设 cand 是名人
int cand = 0;
for (int other = 1; other < n; other++) {
if (!knows(other, cand) || knows(cand, other)) {
// cand 不可能是名人,排除
// 假设 other 是名人
cand = other;
} else {
// other 不可能是名人,排除
// 什么都不用做,继续假设 cand 是名人
}
}
// 现在的 cand 是排除的最后结果,但不能保证一定是名人
for (int other = 0; other < n; other++) {
if (cand == other) continue;
// 需要保证其他人都认识 cand,且 cand 不认识任何其他人
if (!knows(other, cand) || knows(cand, other)) {
return -1;
}
}
return cand;
}我们之前的解法用到了 LinkedList 充当一个队列,用于存储候选人集合,而这个优化解法利用 other 和 cand 的交替变化,模拟了我们之前操作队列的过程,避免了使用额外的存储空间。
现在,解决名人问题的解法时间复杂度为 O(N),空间复杂度为 O(1),已经是最优解法了。
引用本文的文章
_____________
《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复「全家桶」可下载配套 PDF 和刷题全家桶:




