基本套路
- 判断奇偶性: X & 1 == 1 => 奇数,== 0 => 偶数
- 把最低位的 1 清 0 => X = X & (X-1)
- 得到最低位的 1 比如 1100 返回 100 => X & -X
- 把 X 最右边的 n 位清 0 => X & (~0 << n)
- 获取 X 的第 n 位值 => (X >> n) & 1
- 获取 X 的第 n 位的幂值 => X & (1 << (n-1)) ???
- 仅将第 n 位置为 1 => X | (1 << n)
- 仅将第 n 位置为 0 => X & (~(1 << n))
- 将 X 最高位至 n 位(含)清 0 => X & ((1 << n) - 1)
- 将第 n 位至第 0 位(含)清 0 => X & (~((1 << (n + 1)) - 1))
异或
X ^ 0 = X X ^ 1(全 1) = ~X(取反),1(全 1)= ~0 X ^ (~X) = 1(全 1) X ^ X = 0 a ^ b = c => a ^ c = b, b ^ c = a a ^ b ^ c = a ^ (b ^ c) = (a ^ b) ^ c
统计二进制表示中末尾 0 的个数
以下图为例:01101000 返回 3。
方法一:按位取
while((x & (1<<count)) == 0)
count += 1;
方法二:找到 1000(二进制表示),取 log2
x = x & (-x) // -x在计算机中以补码表示,下图中的-X+1
log2(x)
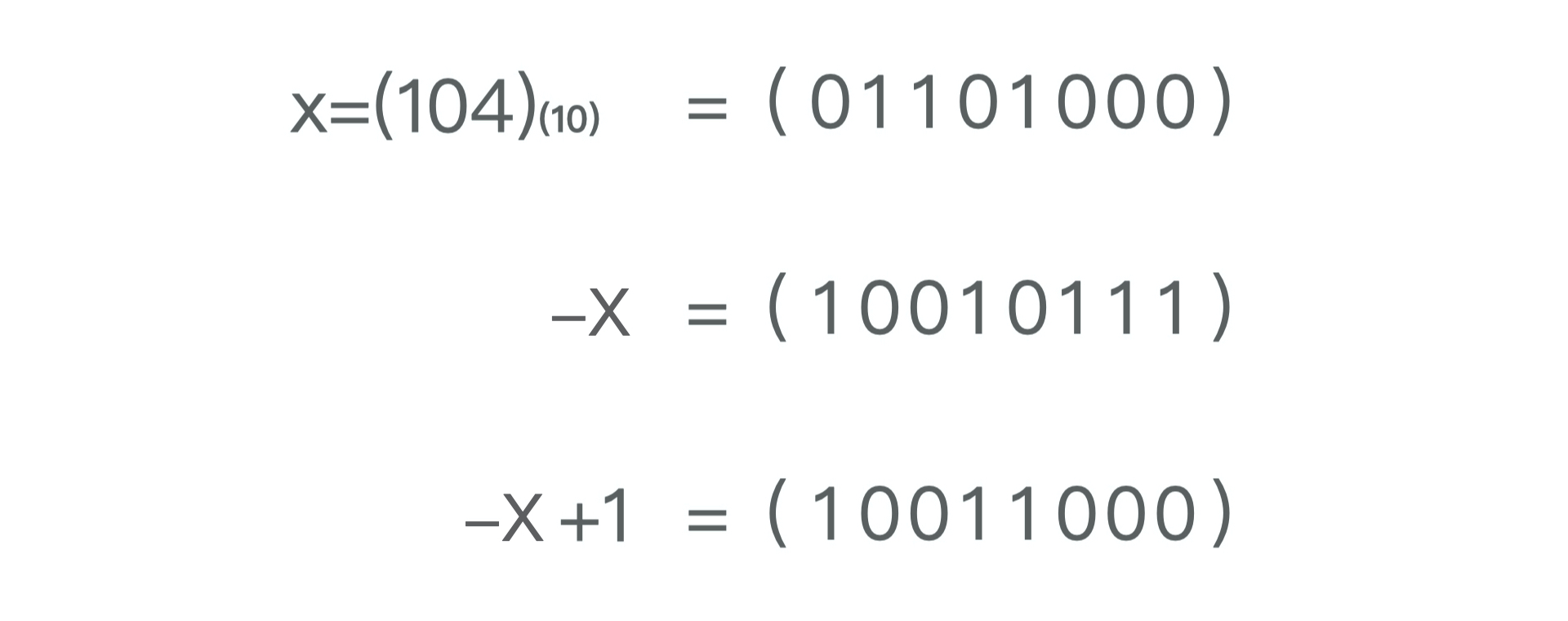
方法三: