参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
bellman_ford之单源有限最短路
【题目描述】
某国为促进城市间经济交流,决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市,通过道路网络连接,网络中的道路仅允许从某个城市单向通行到另一个城市,不能反向通行。
网络中的道路都有各自的运输成本和政府补贴,道路的权值计算方式为:运输成本 - 政府补贴。
权值为正表示扣除了政府补贴后运输货物仍需支付的费用;
权值为负则表示政府的补贴超过了支出的运输成本,实际表现为运输过程中还能赚取一定的收益。
请计算在最多经过 k 个城市的条件下,从城市 src 到城市 dst 的最低运输成本。
【输入描述】
第一行包含两个正整数,第一个正整数 n 表示该国一共有 n 个城市,第二个整数 m 表示这些城市中共有 m 条道路。
接下来为 m 行,每行包括三个整数,s、t 和 v,表示 s 号城市运输货物到达 t 号城市,道路权值为 v。
最后一行包含三个正整数,src、dst、和 k,src 和 dst 为城市编号,从 src 到 dst 经过的城市数量限制。
【输出描述】
输出一个整数,表示从城市 src 到城市 dst 的最低运输成本,如果无法在给定经过城市数量限制下找到从 src 到 dst 的路径,则输出 “unreachable”,表示不存在符合条件的运输方案。
输入示例:
6 7
1 2 1
2 4 -3
2 5 2
1 3 5
3 5 1
4 6 4
5 6 -2
2 6 1
输出示例:
0
思路
本题为单源有限最短路问题,同样是 kama94.城市间货物运输I 延伸题目。
注意题目中描述是 最多经过 k 个城市的条件下,而不是一定经过k个城市,也可以经过的城市数量比k小,但要最短的路径。
在 kama94.城市间货物运输I 中我们讲了:对所有边松弛一次,相当于计算 起点到达 与起点一条边相连的节点 的最短距离。
节点数量为n,起点到终点,最多是 n-1 条边相连。 那么对所有边松弛 n-1 次 就一定能得到 起点到达 终点的最短距离。
(如果对以上讲解看不懂,建议详看 kama94.城市间货物运输I )
本题是最多经过 k 个城市, 那么是 k + 1条边相连的节点。 这里可能有录友想不懂为什么是k + 1,来看这个图:
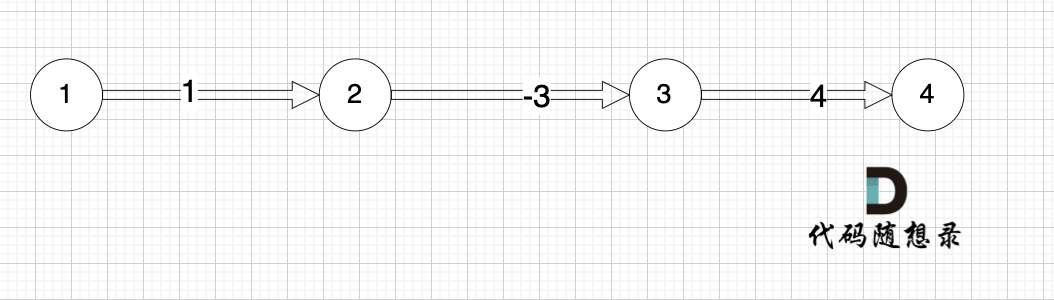
图中,节点1 最多已经经过2个节点 到达节点4,那么中间是有多少条边呢,是 3 条边对吧。
所以本题就是求:起点最多经过k + 1 条边到达终点的最短距离。
对所有边松弛一次,相当于计算 起点到达 与起点一条边相连的节点 的最短距离,那么对所有边松弛 k + 1次,就是求 起点到达 与起点k + 1条边相连的节点的 最短距离。
注意: 本题是 kama94.城市间货物运输I 的拓展题,如果对 bellman_ford 没有深入了解,强烈建议先看 kama94.城市间货物运输I 再做本题。
理解以上内容,其实本题代码就很容易了,bellman_ford 标准写法是松弛 n-1 次,本题就松弛 k + 1次就好。
此时我们可以写出如下代码:
// 版本一
#include <iostream>
#include <vector>
#include <list>
#include <climits>
using namespace std;
int main() {
int src, dst,k ,p1, p2, val ,m , n;
cin >> n >> m;
vector<vector<int>> grid;
for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
// p1 指向 p2,权值为 val
grid.push_back({p1, p2, val});
}
cin >> src >> dst >> k;
vector<int> minDist(n + 1 , INT_MAX);
minDist[src] = 0;
for (int i = 1; i <= k + 1; i++) { // 对所有边松弛 k + 1次
for (vector<int> &side : grid) {
int from = side[0];
int to = side[1];
int price = side[2];
if (minDist[from] != INT_MAX && minDist[to] > minDist[from] + price) minDist[to] = minDist[from] + price;
}
}
if (minDist[dst] == INT_MAX) cout << "unreachable" << endl; // 不能到达终点
else cout << minDist[dst] << endl; // 到达终点最短路径
}
以上代码 标准 bellman_ford 写法,松弛 k + 1次,看上去没什么问题。
但大家提交后,居然没通过!
这是为什么呢?
接下来我们拿这组数据来举例:
4 4
1 2 -1
2 3 1
3 1 -1
3 4 1
1 4 3
(注意上面的示例是有负权回路的,只有带负权回路的图才能说明问题)
负权回路是指一条道路的总权值为负,这样的回路使得通过反复经过回路中的道路,理论上可以无限地减少总成本或无限地增加总收益。
正常来说,这组数据输出应该是 1,但以上代码输出的是 -2。
在讲解原因的时候,强烈建议大家,先把 minDist数组打印出来,看看minDist数组是不是按照自己的想法变化的,这样更容易理解我接下来的讲解内容。 (一定要动手,实践出真实,脑洞模拟不靠谱)
打印的代码可以是这样:
#include <iostream>
#include <vector>
#include <list>
#include <climits>
using namespace std;
int main() {
int src, dst,k ,p1, p2, val ,m , n;
cin >> n >> m;
vector<vector<int>> grid;
for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
// p1 指向 p2,权值为 val
grid.push_back({p1, p2, val});
}
cin >> src >> dst >> k;
vector<int> minDist(n + 1 , INT_MAX);
minDist[src] = 0;
for (int i = 1; i <= k + 1; i++) { // 对所有边松弛 k + 1次
for (vector<int> &side : grid) {
int from = side[0];
int to = side[1];
int price = side[2];
if (minDist[from] != INT_MAX && minDist[to] > minDist[from] + price) minDist[to] = minDist[from] + price;
}
// 打印 minDist 数组
for (int j = 1; j <= n; j++) cout << minDist[j] << " ";
cout << endl;
}
if (minDist[dst] == INT_MAX) cout << "unreachable" << endl; // 不能到达终点
else cout << minDist[dst] << endl; // 到达终点最短路径
}
接下来,我按照上面的示例带大家 画图举例 对所有边松弛一次 的效果图。
起点为节点1, 起点到起点的距离为0,所以 minDist[1] 初始化为0 ,如图:
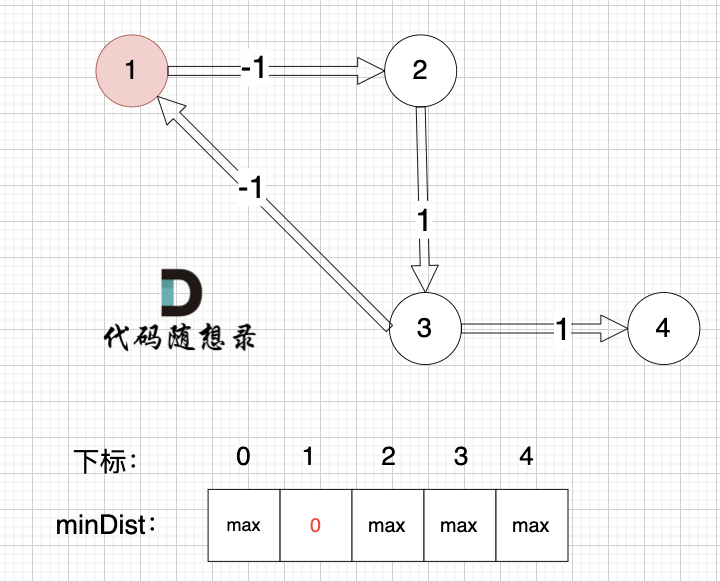
其他节点对应的minDist初始化为max,因为我们要求最小距离,那么还没有计算过的节点 默认是一个最大数,这样才能更新最小距离。
当我们开始对所有边开始第一次松弛:
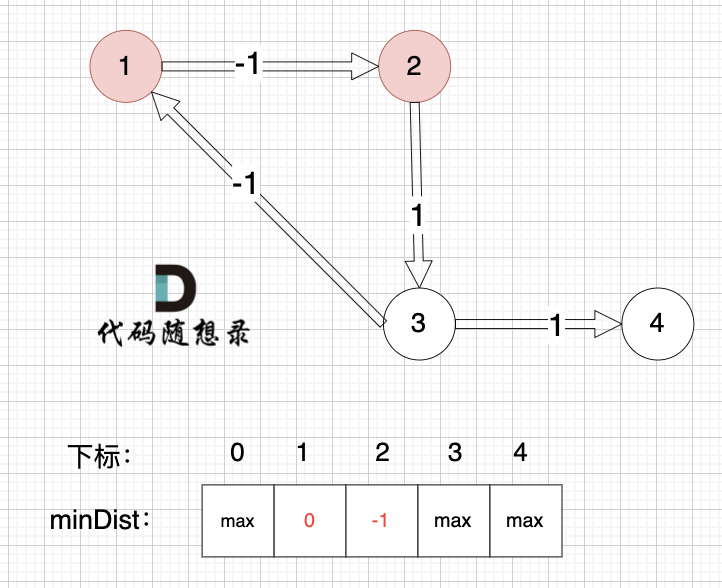
边:节点1 -> 节点2,权值为-1 ,minDist[2] > minDist[1] + (-1),更新 minDist[2] = minDist[1] + (-1) = 0 - 1 = -1 ,如图:
边:节点2 -> 节点3,权值为1 ,minDist[3] > minDist[2] + 1 ,更新 minDist[3] = minDist[2] + 1 = -1 + 1 = 0 ,如图:
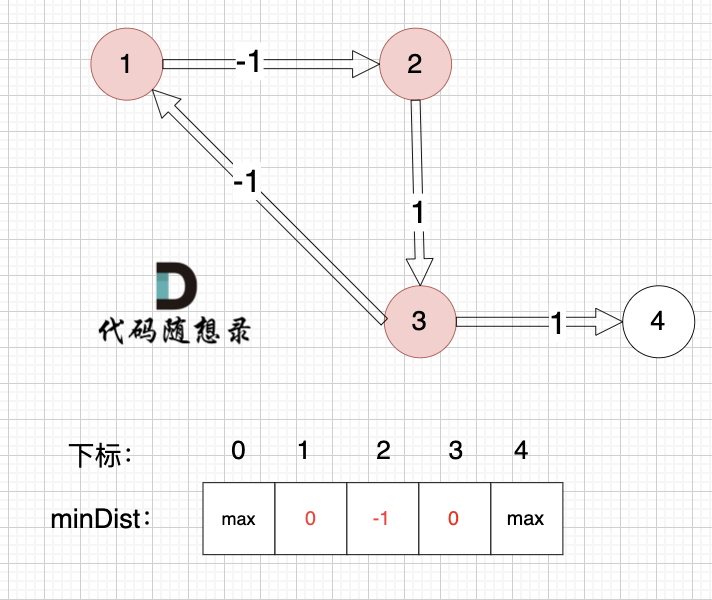
边:节点3 -> 节点1,权值为-1 ,minDist[1] > minDist[3] + (-1),更新 minDist[1] = 0 + (-1) = -1 ,如图:

边:节点3 -> 节点4,权值为1 ,minDist[4] > minDist[3] + 1,更新 minDist[4] = 0 + 1 = 1 ,如图:
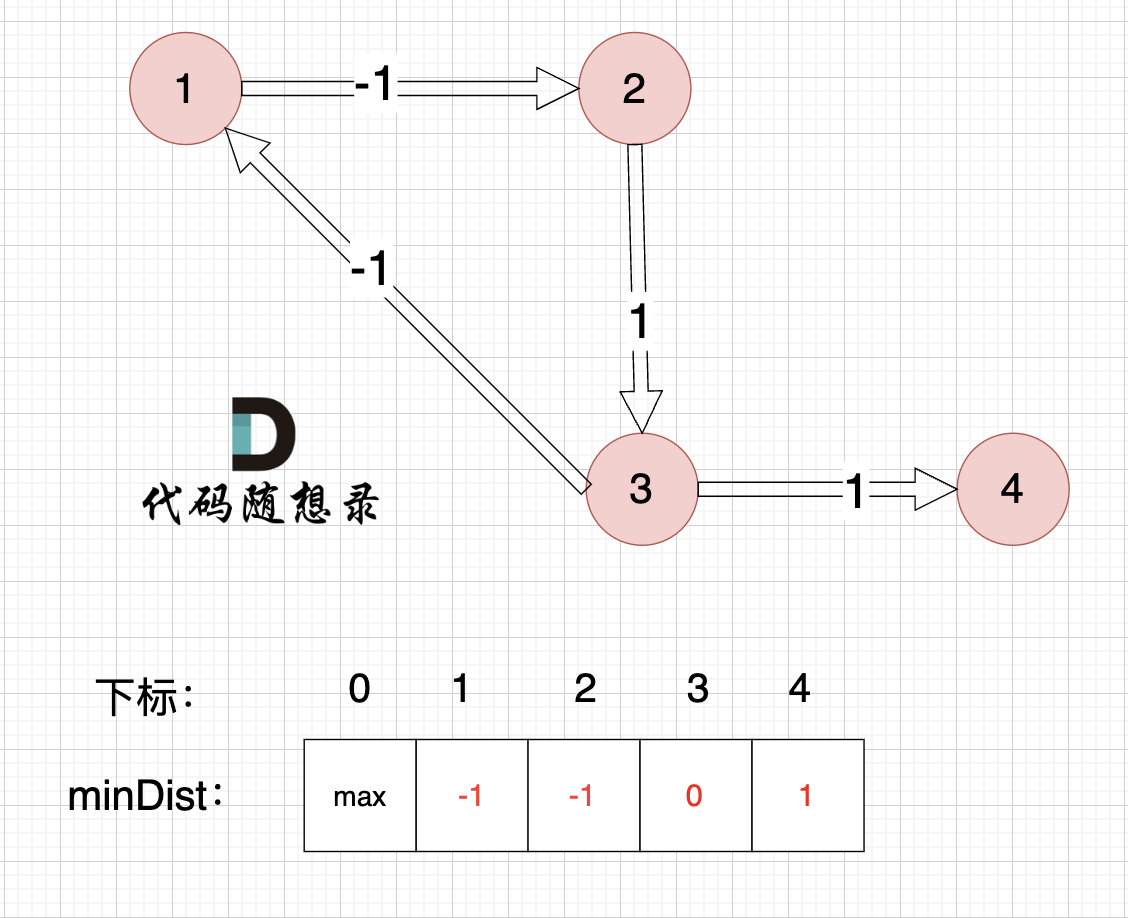
以上是对所有边进行的第一次松弛,最后 minDist数组为 :-1 -1 0 1 ,(从下标1算起)
后面几次松弛我就不挨个画图了,过程大同小异,我直接给出minDist数组的变化:
所有边进行的第二次松弛,minDist数组为 : -2 -2 -1 0 所有边进行的第三次松弛,minDist数组为 : -3 -3 -2 -1 所有边进行的第四次松弛,minDist数组为 : -4 -4 -3 -2 (本示例中k为3,所以松弛4次)
最后计算的结果minDist[4] = -2,即 起点到 节点4,最多经过 3 个节点的最短距离是 -2,但 正确的结果应该是 1,即路径:节点1 -> 节点2 -> 节点3 -> 节点4。
理论上来说,对所有边松弛一次,相当于计算 起点到达 与起点一条边相连的节点 的最短距离。
对所有边松弛两次,相当于计算 起点到达 与起点两条边相连的节点的最短距离。
对所有边松弛三次,以此类推。
但在对所有边松弛第一次的过程中,大家会发现,不仅仅 与起点一条边相连的节点更新了,所有节点都更新了。
而且对所有边的后面几次松弛,同样是更新了所有的节点,说明 至多经过k 个节点 这个限制 根本没有限制住,每个节点的数值都被更新了。
这是为什么?
在上面画图距离中,对所有边进行第一次松弛,在计算 边(节点2 -> 节点3) 的时候,更新了 节点3。

理论上来说节点3 应该在对所有边第二次松弛的时候才更新。 这因为当时是基于已经计算好的 节点2(minDist[2])来做计算了。
minDist[2]在计算边:(节点1 -> 节点2)的时候刚刚被赋值为 -1。
这样就造成了一个情况,即:计算minDist数组的时候,基于了本次松弛的 minDist数值,而不是上一次 松弛时候minDist的数值。
所以在每次计算 minDist 时候,要基于 对所有边上一次松弛的 minDist 数值才行,所以我们要记录上一次松弛的minDist。
代码修改如下: (关键地方已经注释)
// 版本二
#include <iostream>
#include <vector>
#include <list>
#include <climits>
using namespace std;
int main() {
int src, dst,k ,p1, p2, val ,m , n;
cin >> n >> m;
vector<vector<int>> grid;
for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
grid.push_back({p1, p2, val});
}
cin >> src >> dst >> k;
vector<int> minDist(n + 1 , INT_MAX);
minDist[src] = 0;
vector<int> minDist_copy(n + 1); // 用来记录上一次遍历的结果
for (int i = 1; i <= k + 1; i++) {
minDist_copy = minDist; // 获取上一次计算的结果
for (vector<int> &side : grid) {
int from = side[0];
int to = side[1];
int price = side[2];
// 注意使用 minDist_copy 来计算 minDist
if (minDist_copy[from] != INT_MAX && minDist[to] > minDist_copy[from] + price) {
minDist[to] = minDist_copy[from] + price;
}
}
}
if (minDist[dst] == INT_MAX) cout << "unreachable" << endl; // 不能到达终点
else cout << minDist[dst] << endl; // 到达终点最短路径
}
- 时间复杂度: O(K * E) , K为至多经过K个节点,E为图中边的数量
- 空间复杂度: O(N) ,即 minDist 数组所开辟的空间
拓展一(边的顺序的影响)
其实边的顺序会影响我们每一次拓展的结果。
我来给大家举个例子。
我上面讲解中,给出的示例是这样的:
4 4
1 2 -1
2 3 1
3 1 -1
3 4 1
1 4 3
我将示例中边的顺序改一下,给成:
4 4
3 1 -1
3 4 1
2 3 1
1 2 -1
1 4 3
所构成是图是一样的,都是如下的这个图,但给出的边的顺序是不一样的。
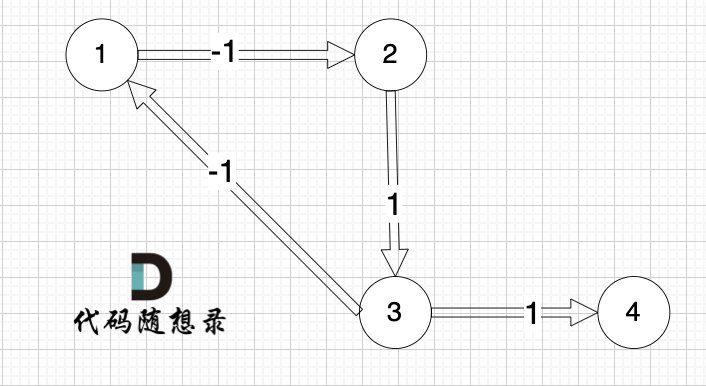
再用版本一的代码是运行一下,发现结果输出是 1, 是对的。

分明刚刚输出的结果是 -2,是错误的,怎么 一样的图,这次输出的结果就对了呢?
其实这是和示例中给出的边的顺序是有关的,
我们按照修改后的示例再来模拟 对所有边的第一次拓展情况。
初始化:
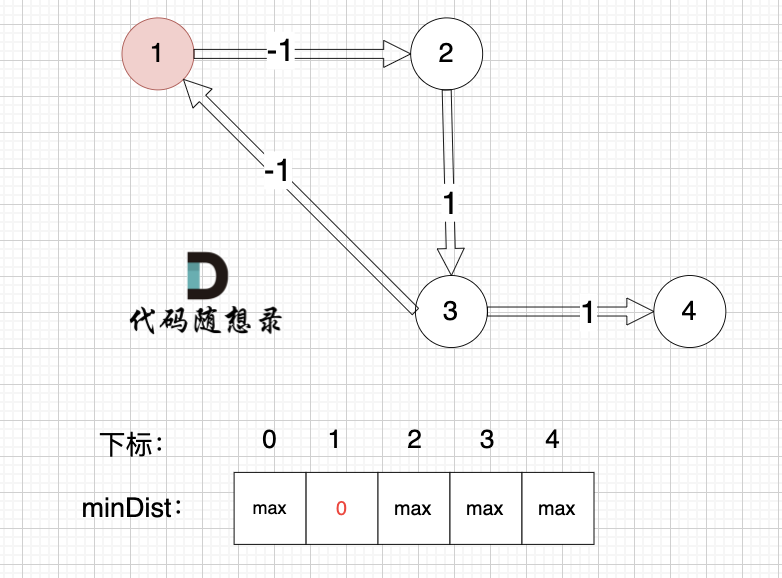
边:节点3 -> 节点1,权值为-1 ,节点3还没有被计算过,节点1 不更新。
边:节点3 -> 节点4,权值为1 ,节点3还没有被计算过,节点4 不更新。
边:节点2 -> 节点3,权值为 1 ,节点2还没有被计算过,节点3 不更新。
边:节点1 -> 节点2,权值为 -1 ,minDist[2] > minDist[1] + (-1),更新 minDist[2] = 0 + (-1) = -1 ,如图:
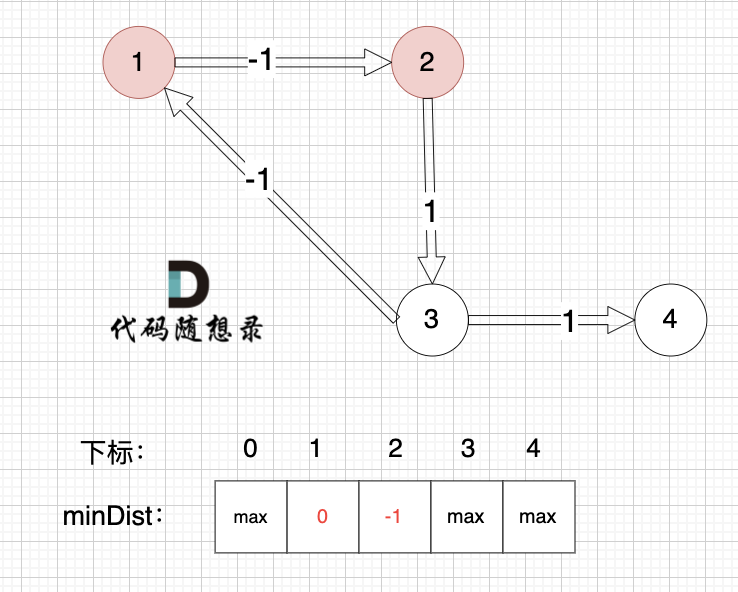
以上是对所有边 松弛一次的状态。
可以发现 同样的图,边的顺序不一样,使用版本一的代码 每次松弛更新的节点也是不一样的。
而边的顺序是随机的,是题目给我们的,所以本题我们才需要 记录上一次松弛的minDist,来保障 每一次对所有边松弛的结果。
拓展二(本题本质)
那么前面讲解过的 94.城市间货物运输I 和 95.城市间货物运输II 也是bellman_ford经典算法,也没使用 minDist_copy,怎么就没问题呢?
如果没看过我上面这两篇讲解的话,建议详细学习上面两篇,再看我下面讲的区别,否则容易看不懂。
94.城市间货物运输I, 是没有 负权回路的,那么 多松弛多少次,对结果都没有影响。
求 节点1 到 节点n 的最短路径,松弛n-1 次就够了,松弛 大于 n-1次,结果也不会变。
那么在对所有边进行第一次松弛的时候,如果基于 本次计算的 minDist 来计算 minDist (相当于多做松弛了),也是对最终结果没影响。
95.城市间货物运输II 是判断是否有 负权回路,一旦有负权回路, 对所有边松弛 n-1 次以后,在做松弛 minDist 数值一定会变,根据这一点来判断是否有负权回路。
所以,95.城市间货物运输II 只需要判断minDist数值变化了就行,而 minDist 的数值对不对,并不是我们关心的。
那么本题 为什么计算minDist 一定要基于上次 的 minDist 数值。
其关键在于本题的两个因素:
- 本题可以有负权回路,说明只要多做松弛,结果是会变的。
- 本题要求最多经过k个节点,对松弛次数是有限制的。
如果本题中 没有负权回路的测试用例, 那版本一的代码就可以过了,也就不用我费这么大口舌去讲解的这个坑了。
拓展三(SPFA)
本题也可以用 SPFA来做,关于 SPFA ,已经在这里 0094.城市间货物运输I-SPFA 有详细讲解。
使用SPFA算法解决本题的时候,关键在于 如何控制松弛k次。
其实实现不难,但有点技巧,可以用一个变量 que_size 记录每一轮松弛入队列的所有节点数量。
下一轮松弛的时候,就把队列里 que_size 个节点都弹出来,就是上一轮松弛入队列的节点。
代码如下(详细注释)
#include <iostream>
#include <vector>
#include <queue>
#include <list>
#include <climits>
using namespace std;
struct Edge { //邻接表
int to; // 链接的节点
int val; // 边的权重
Edge(int t, int w): to(t), val(w) {} // 构造函数
};
int main() {
int n, m, p1, p2, val;
cin >> n >> m;
vector<list<Edge>> grid(n + 1); // 邻接表
// 将所有边保存起来
for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
// p1 指向 p2,权值为 val
grid[p1].push_back(Edge(p2, val));
}
int start, end, k;
cin >> start >> end >> k;
k++;
vector<int> minDist(n + 1 , INT_MAX);
vector<int> minDist_copy(n + 1); // 用来记录每一次遍历的结果
minDist[start] = 0;
queue<int> que;
que.push(start); // 队列里放入起点
int que_size;
while (k-- && !que.empty()) {
minDist_copy = minDist; // 获取上一次计算的结果
que_size = que.size(); // 记录上次入队列的节点个数
while (que_size--) { // 上一轮松弛入队列的节点,这次对应的边都要做松弛
int node = que.front(); que.pop();
for (Edge edge : grid[node]) {
int from = node;
int to = edge.to;
int price = edge.val;
if (minDist[to] > minDist_copy[from] + price) {
minDist[to] = minDist_copy[from] + price;
que.push(to);
}
}
}
}
if (minDist[end] == INT_MAX) cout << "unreachable" << endl;
else cout << minDist[end] << endl;
}
时间复杂度: O(K * H) H 为不确定数,取决于 图的稠密度,但H 一定是小于等于 E 的
关于 SPFA的是时间复杂度分析,我在0094.城市间货物运输I-SPFA 有详细讲解
但大家会发现,以上代码大家提交后,怎么耗时这么多?
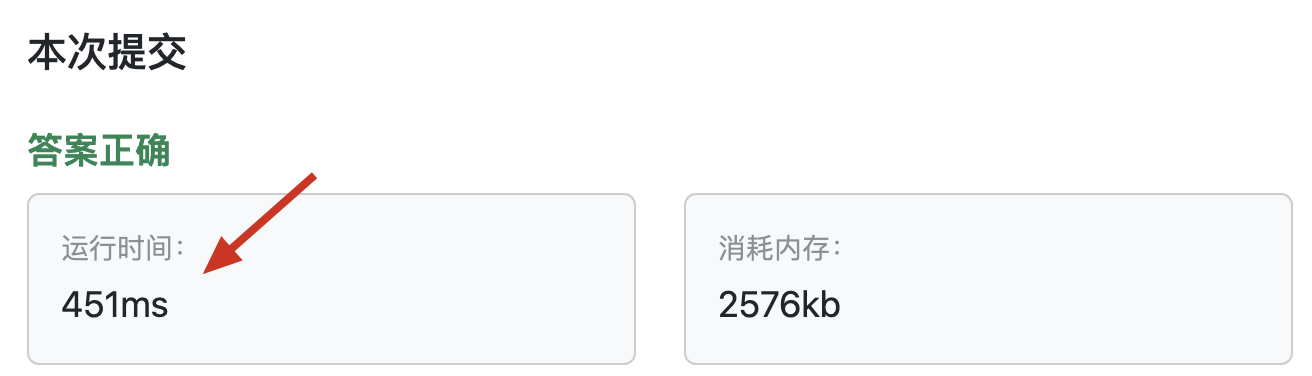
理论上,SPFA的时间复杂度不是要比 bellman_ford 更优吗?
怎么耗时多了这么多呢?
以上代码有一个可以改进的点,每一轮松弛中,重复节点可以不用入队列。
因为重复节点入队列,下次从队列里取节点的时候,该节点要取很多次,而且都是重复计算。
所以代码可以优化成这样:
#include <iostream>
#include <vector>
#include <queue>
#include <list>
#include <climits>
using namespace std;
struct Edge { //邻接表
int to; // 链接的节点
int val; // 边的权重
Edge(int t, int w): to(t), val(w) {} // 构造函数
};
int main() {
int n, m, p1, p2, val;
cin >> n >> m;
vector<list<Edge>> grid(n + 1); // 邻接表
// 将所有边保存起来
for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
// p1 指向 p2,权值为 val
grid[p1].push_back(Edge(p2, val));
}
int start, end, k;
cin >> start >> end >> k;
k++;
vector<int> minDist(n + 1 , INT_MAX);
vector<int> minDist_copy(n + 1); // 用来记录每一次遍历的结果
minDist[start] = 0;
queue<int> que;
que.push(start); // 队列里放入起点
int que_size;
while (k-- && !que.empty()) {
vector<bool> visited(n + 1, false); // 每一轮松弛中,控制节点不用重复入队列
minDist_copy = minDist;
que_size = que.size();
while (que_size--) {
int node = que.front(); que.pop();
for (Edge edge : grid[node]) {
int from = node;
int to = edge.to;
int price = edge.val;
if (minDist[to] > minDist_copy[from] + price) {
minDist[to] = minDist_copy[from] + price;
if(visited[to]) continue; // 不用重复放入队列,但需要重复松弛,所以放在这里位置
visited[to] = true;
que.push(to);
}
}
}
}
if (minDist[end] == INT_MAX) cout << "unreachable" << endl;
else cout << minDist[end] << endl;
}以上代码提交后,耗时情况:
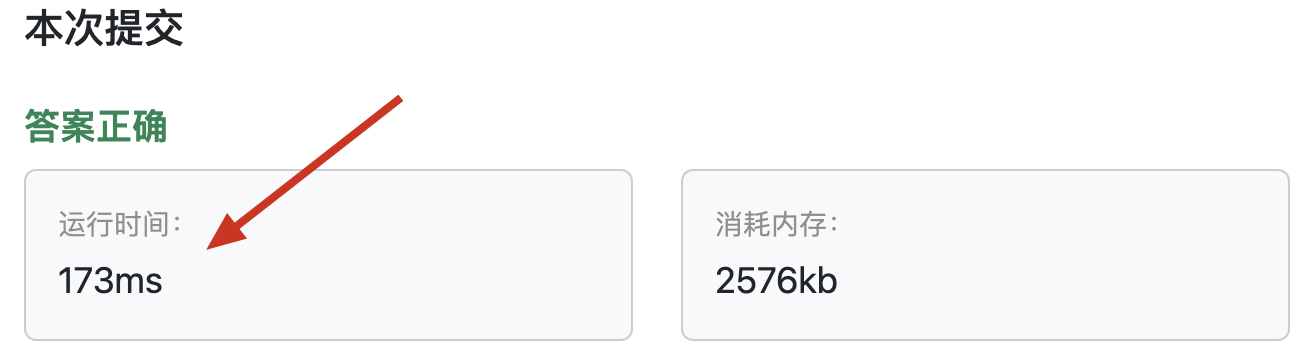
大家发现 依然远比 bellman_ford 的代码版本 耗时高。
这又是为什么呢?
对于后台数据,我特别制作的一个稠密大图,该图有250个节点和10000条边, 在这种情况下, SPFA 的时间复杂度 是接近与 bellman_ford的。
但因为 SPFA 节点的进出队列操作,耗时很大,所以相同的时间复杂度的情况下,SPFA 实际上更耗时了。
这一点我在 0094.城市间货物运输I-SPFA 有分析,感兴趣的录友再回头去看看。
拓展四(能否用dijkstra)
本题能否使用 dijkstra 算法呢?
dijkstra 是贪心的思路 每一次搜索都只会找距离源点最近的非访问过的节点。
如果限制最多访问k个节点,那么 dijkstra 未必能在有限次就能到达终点,即使在经过k个节点确实可以到达终点的情况下。
这么说大家会感觉有点抽象,我用 dijkstra朴素版精讲 里的示例在举例说明: (如果没看过我讲的dijkstra朴素版精讲,建议去仔细看一下,否则下面讲解容易看不懂)
在以下这个图中,求节点1 到 节点7 最多经过2个节点 的最短路是多少呢?

最短路显然是:

最多经过2个节点,也就是3条边相连的路线:节点1 -> 节点2 -> 节点6-> 节点7
如果是 dijkstra 求解的话,求解过程是这样的: (下面是dijkstra的模拟过程,我精简了很多,如果看不懂,一定要先看dijkstra朴素版精讲)
初始化如图所示:

找距离源点最近且没有被访问过的节点,先找节点1

距离源点最近且没有被访问过的节点,找节点2:
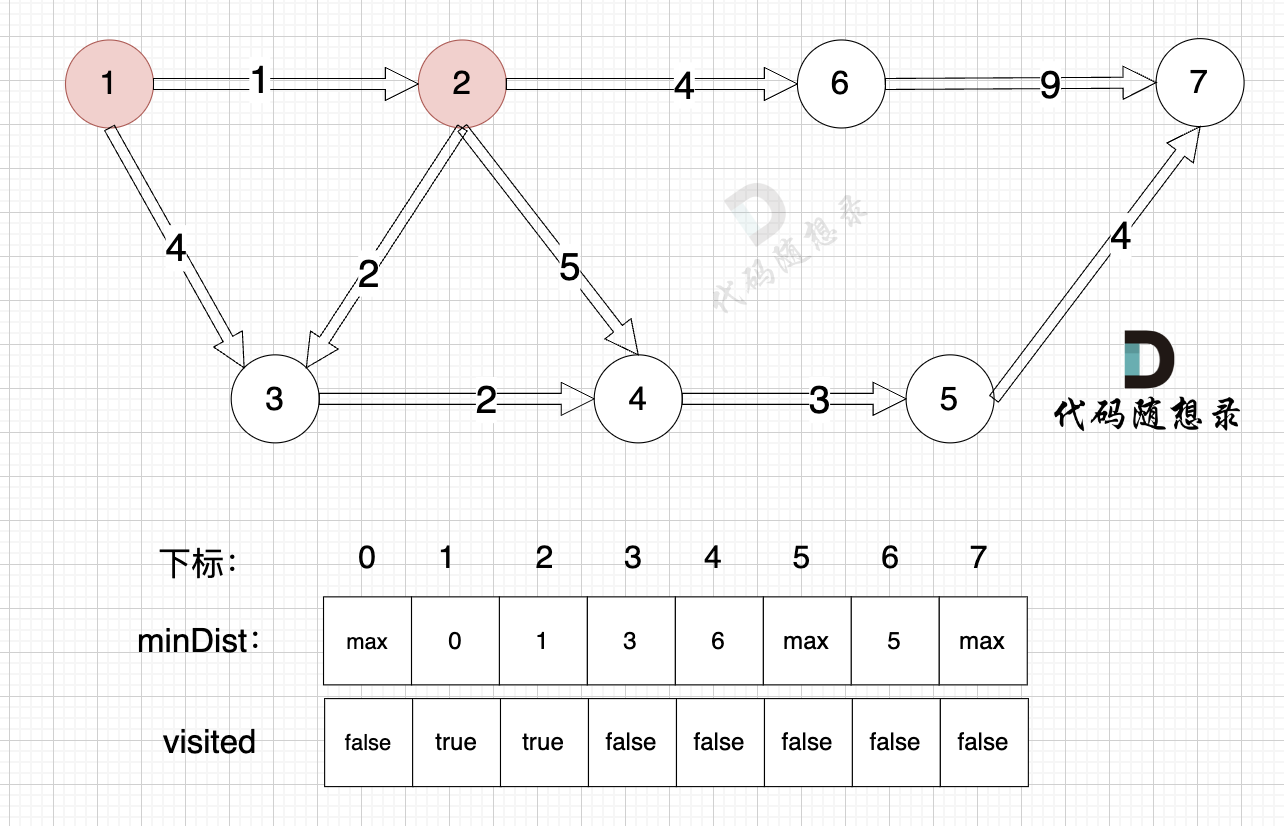
距离源点最近且没有被访问过的节点,找到节点3:

距离源点最近且没有被访问过的节点,找到节点4:
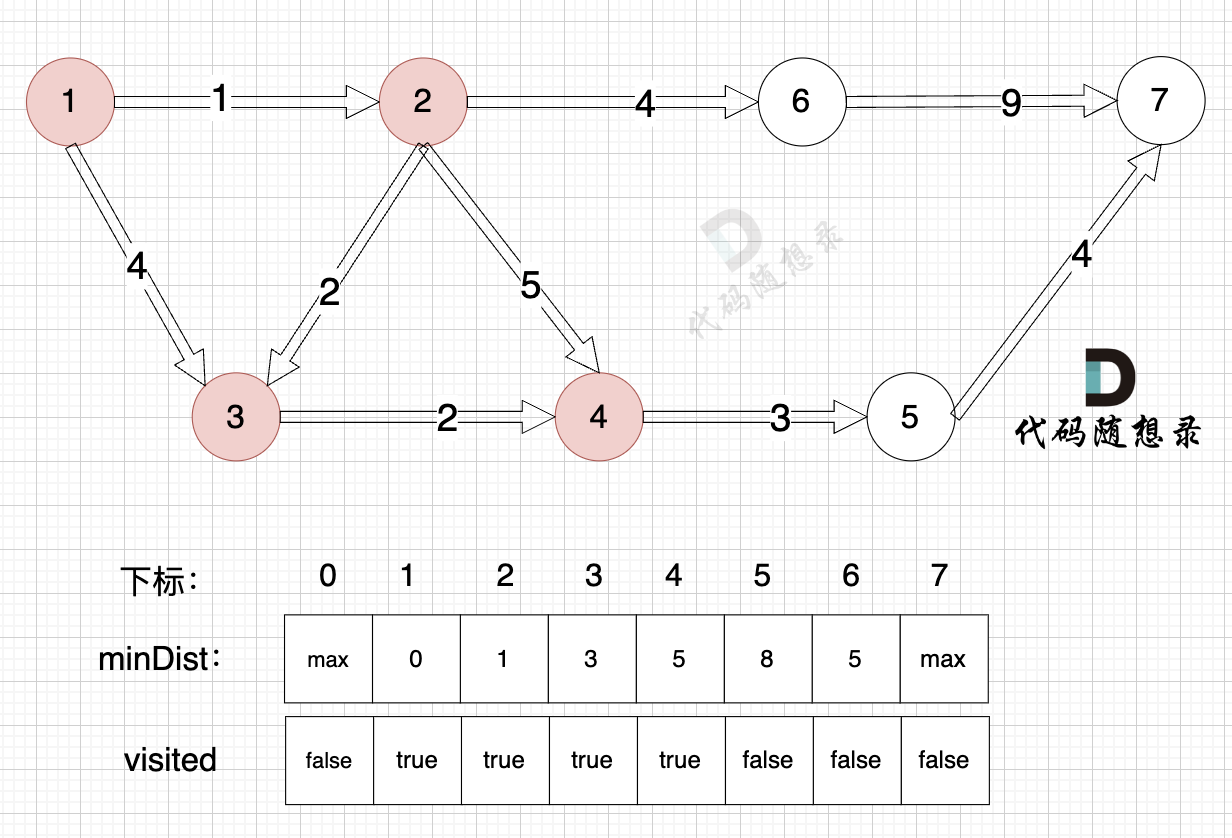
此时最多经过2个节点的搜索就完毕了,但结果中minDist[7] (即节点7的结果)并没有被更。
那么 dijkstra 会告诉我们 节点1 到 节点7 最多经过2个节点的情况下是不可到达的。
通过以上模拟过程,大家应该能感受到 dijkstra 贪心的过程,正是因为 贪心,所以 dijkstra 找不到 节点1 -> 节点2 -> 节点6-> 节点7 这条路径。
总结
本题是单源有限最短路问题,也是 bellman_ford的一个拓展问题,如果理解bellman_ford 其实思路比较容易理解,但有很多细节。
例如 为什么要用 minDist_copy 来记录上一轮 松弛的结果。 这也是本篇我为什么花了这么大篇幅讲解的关键所在。
接下来,还给大家做了四个拓展:
- 边的顺序的影响
- 本题的本质
- SPFA的解法
- 能否用dijkstra
学透了以上四个拓展,相信大家会对bellman_ford有更深入的理解。
其他语言版本
Java
import java.util.*;
public class Main {
// 基于Bellman_for一般解法解决单源最短路径问题
// Define an inner class Edge
static class Edge {
int from;
int to;
int val;
public Edge(int from, int to, int val) {
this.from = from;
this.to = to;
this.val = val;
}
}
public static void main(String[] args) {
// Input processing
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
List<Edge> graph = new ArrayList<>();
for (int i = 0; i < m; i++) {
int from = sc.nextInt();
int to = sc.nextInt();
int val = sc.nextInt();
graph.add(new Edge(from, to, val));
}
int src = sc.nextInt();
int dst = sc.nextInt();
int k = sc.nextInt();
int[] minDist = new int[n + 1];
int[] minDistCopy;
Arrays.fill(minDist, Integer.MAX_VALUE);
minDist[src] = 0;
for (int i = 0; i < k + 1; i++) { // Relax all edges k + 1 times
minDistCopy = Arrays.copyOf(minDist, n + 1);
for (Edge edge : graph) {
int from = edge.from;
int to = edge.to;
int val = edge.val;
// Use minDistCopy to calculate minDist
if (minDistCopy[from] != Integer.MAX_VALUE && minDist[to] > minDistCopy[from] + val) {
minDist[to] = minDistCopy[from] + val;
}
}
}
// Output printing
if (minDist[dst] == Integer.MAX_VALUE) {
System.out.println("unreachable");
} else {
System.out.println(minDist[dst]);
}
}
}
class Edge {
public int u; // 边的端点1
public int v; // 边的端点2
public int val; // 边的权值
public Edge() {
}
public Edge(int u, int v) {
this.u = u;
this.v = v;
this.val = 0;
}
public Edge(int u, int v, int val) {
this.u = u;
this.v = v;
this.val = val;
}
}
/**
* SPFA算法(版本3):处理含【负权回路】的有向图的最短路径问题
* bellman_ford(版本3) 的队列优化算法版本
* 限定起点、终点、至多途径k个节点
*/
public class SPFAForSSSP {
/**
* SPFA算法
*
* @param n 节点个数[1,n]
* @param graph 邻接表
* @param startIdx 开始节点(源点)
*/
public static int[] spfa(int n, List<List<Edge>> graph, int startIdx, int k) {
// 定义最大范围
int maxVal = Integer.MAX_VALUE;
// minDist[i] 源点到节点i的最短距离
int[] minDist = new int[n + 1]; // 有效节点编号范围:[1,n]
Arrays.fill(minDist, maxVal); // 初始化为maxVal
minDist[startIdx] = 0; // 设置源点到源点的最短路径为0
// 定义queue记录每一次松弛更新的节点
Queue<Integer> queue = new LinkedList<>();
queue.offer(startIdx); // 初始化:源点开始(queue和minDist的更新是同步的)
// SPFA算法核心:只对上一次松弛的时候更新过的节点关联的边进行松弛操作
while (k + 1 > 0 && !queue.isEmpty()) { // 限定松弛 k+1 次
int curSize = queue.size(); // 记录当前队列节点个数(上一次松弛更新的节点个数,用作分层统计)
while (curSize-- > 0) { //分层控制,限定本次松弛只针对上一次松弛更新的节点,不对新增的节点做处理
// 记录当前minDist状态,作为本次松弛的基础
int[] minDist_copy = Arrays.copyOfRange(minDist, 0, minDist.length);
// 取出节点
int cur = queue.poll();
// 获取cur节点关联的边,进行松弛操作
List<Edge> relateEdges = graph.get(cur);
for (Edge edge : relateEdges) {
int u = edge.u; // 与`cur`对照
int v = edge.v;
int weight = edge.val;
if (minDist_copy[u] + weight < minDist[v]) {
minDist[v] = minDist_copy[u] + weight; // 更新
// 队列同步更新(此处有一个针对队列的优化:就是如果已经存在于队列的元素不需要重复添加)
if (!queue.contains(v)) {
queue.offer(v); // 与minDist[i]同步更新,将本次更新的节点加入队列,用做下一个松弛的参考基础
}
}
}
}
// 当次松弛结束,次数-1
k--;
}
// 返回minDist
return minDist;
}
public static void main(String[] args) {
// 输入控制
Scanner sc = new Scanner(System.in);
System.out.println("1.输入N个节点、M条边(u v weight)");
int n = sc.nextInt();
int m = sc.nextInt();
System.out.println("2.输入M条边");
List<List<Edge>> graph = new ArrayList<>(); // 构建邻接表
for (int i = 0; i <= n; i++) {
graph.add(new ArrayList<>());
}
while (m-- > 0) {
int u = sc.nextInt();
int v = sc.nextInt();
int weight = sc.nextInt();
graph.get(u).add(new Edge(u, v, weight));
}
System.out.println("3.输入src dst k(起点、终点、至多途径k个点)");
int src = sc.nextInt();
int dst = sc.nextInt();
int k = sc.nextInt();
// 调用算法
int[] minDist = SPFAForSSSP.spfa(n, graph, src, k);
// 校验起点->终点
if (minDist[dst] == Integer.MAX_VALUE) {
System.out.println("unreachable");
} else {
System.out.println("最短路径:" + minDist[n]);
}
}
}Python
Bellman-Ford方法求解单源有限最短路
def main():
# 輸入
n, m = map(int, input().split())
edges = list()
for _ in range(m):
edges.append(list(map(int, input().split() )))
start, end, k = map(int, input().split())
min_dist = [float('inf') for _ in range(n + 1)]
min_dist[start] = 0
# 只能經過k個城市,所以從起始點到中間有(k + 1)個邊連接
# 需要鬆弛(k + 1)次
for _ in range(k + 1):
update = False
min_dist_copy = min_dist.copy()
for src, desc, w in edges:
if (min_dist_copy[src] != float('inf') and
min_dist_copy[src] + w < min_dist[desc]):
min_dist[desc] = min_dist_copy[src] + w
update = True
if not update:
break
# 輸出
if min_dist[end] == float('inf'):
print('unreachable')
else:
print(min_dist[end])
if __name__ == "__main__":
main()SPFA方法求解单源有限最短路
from collections import deque
from math import inf
def main():
n, m = [int(i) for i in input().split()]
graph = [[] for _ in range(n+1)]
for _ in range(m):
v1, v2, val = [int(i) for i in input().split()]
graph[v1].append([v2, val])
src, dst, k = [int(i) for i in input().split()]
min_dist = [inf for _ in range(n+1)]
min_dist[src] = 0 # 初始化起点的距离
que = deque([src])
while k != -1 and que:
visited = [False for _ in range(n+1)] # 用于保证每次松弛时一个节点最多加入队列一次
que_size = len(que)
temp_dist = min_dist.copy() # 用于记录上一次遍历的结果
for _ in range(que_size):
cur_node = que.popleft()
for next_node, val in graph[cur_node]:
if min_dist[next_node] > temp_dist[cur_node] + val:
min_dist[next_node] = temp_dist[cur_node] + val
if not visited[next_node]:
que.append(next_node)
visited[next_node] = True
k -= 1
if min_dist[dst] == inf:
print("unreachable")
else:
print(min_dist[dst])
if __name__ == "__main__":
main()