参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
prim算法精讲
题目描述:
在世界的某个区域,有一些分散的神秘岛屿,每个岛屿上都有一种珍稀的资源或者宝藏。国王打算在这些岛屿上建公路,方便运输。
不同岛屿之间,路途距离不同,国王希望你可以规划建公路的方案,如何可以以最短的总公路距离将所有岛屿联通起来。
给定一张地图,其中包括了所有的岛屿,以及它们之间的距离。以最小化公路建设长度,确保可以链接到所有岛屿。
输入描述:
第一行包含两个整数V和E,V代表顶点数,E代表边数。顶点编号是从1到V。例如:V=2,一个有两个顶点,分别是1和2。
接下来共有E行,每行三个整数v1,v2和val,v1和v2为边的起点和终点,val代表边的权值。
输出描述:
输出联通所有岛屿的最小路径总距离
输入示例:
7 11
1 2 1
1 3 1
1 5 2
2 6 1
2 4 2
2 3 2
3 4 1
4 5 1
5 6 2
5 7 1
6 7 1
输出示例:
6
解题思路
本题是最小生成树的模板题,那么我们来讲一讲最小生成树。
最小生成树可以使用prim算法也可以使用kruskal算法计算出来。
本篇我们先讲解prim算法。
最小生成树是所有节点的最小连通子图,即:以最小的成本(边的权值)将图中所有节点链接到一起。
图中有n个节点,那么一定可以用n-1条边将所有节点连接到一起。
那么如何选择这n-1条边就是最小生成树算法的任务所在。
例如本题示例中的无向有权图为:
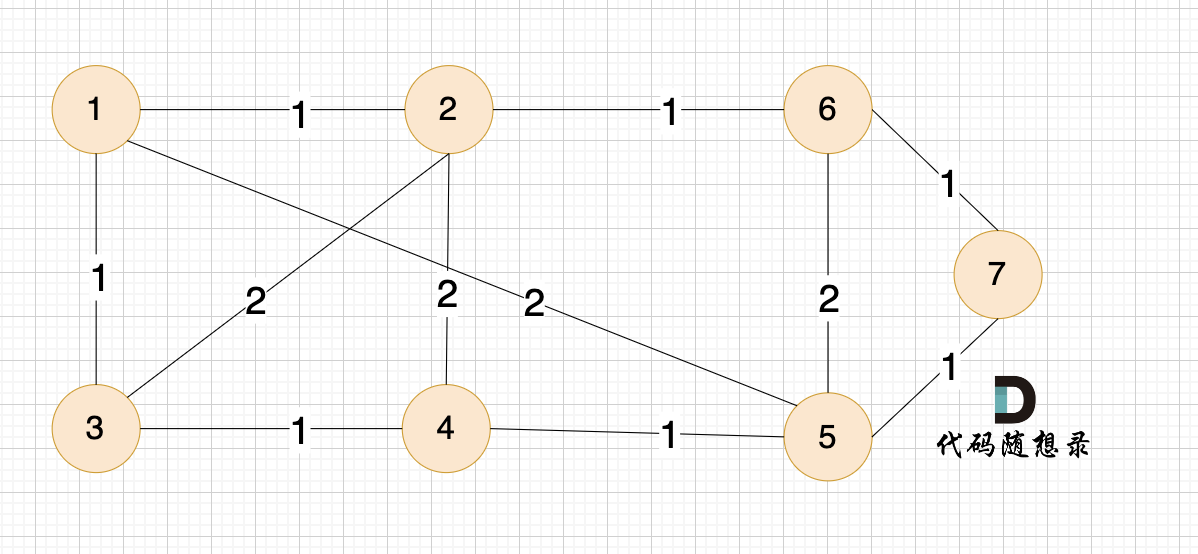
那么在这个图中,如何选取n-1条边使得图中所有节点连接到一起,并且边的权值和最小呢?
(图中为n为7,即7个节点,那么只需要n-1即6条边就可以讲所有顶点连接到一起)
prim算法是从节点的角度采用贪心的策略每次寻找距离最小生成树最近的节点并加入到最小生成树中。
prim算法核心就是三步,我称为prim三部曲,大家一定要熟悉这三步,代码相对会好些很多:
- 第一步,选距离生成树最近节点
- 第二步,最近节点加入生成树
- 第三步,更新非生成树节点到生成树的距离(即更新minDist数组)
现在录友们会对这三步很陌生,不知道这是干啥的,没关系,下面将会画图举例来带大家把这prim三部曲理解到位。
在prim算法中,有一个数组特别重要,这里我起名为:minDist。
刚刚我有讲过“每次寻找距离最小生成树最近的节点并加入到最小生成树中”,那么如何寻找距离最小生成树最近的节点呢?
这就用到了minDist数组,它用来作什么呢?
minDist数组用来记录每一个节点距离最小生成树的最近距离。理解这一点非常重要,这也是prim算法最核心要点所在,很多录友看不懂prim算法的代码,都是因为没有理解透这个数组的含义。
接下来,我们来通过一步一步画图,来带大家巩固prim三部曲以及minDist数组的作用。
(示例中节点编号是从1开始,所以为了让大家看的不晕,minDist数组下标我也从1开始计数,下标0就不使用了,这样下标和节点标号就可以对应上了,避免大家搞混)
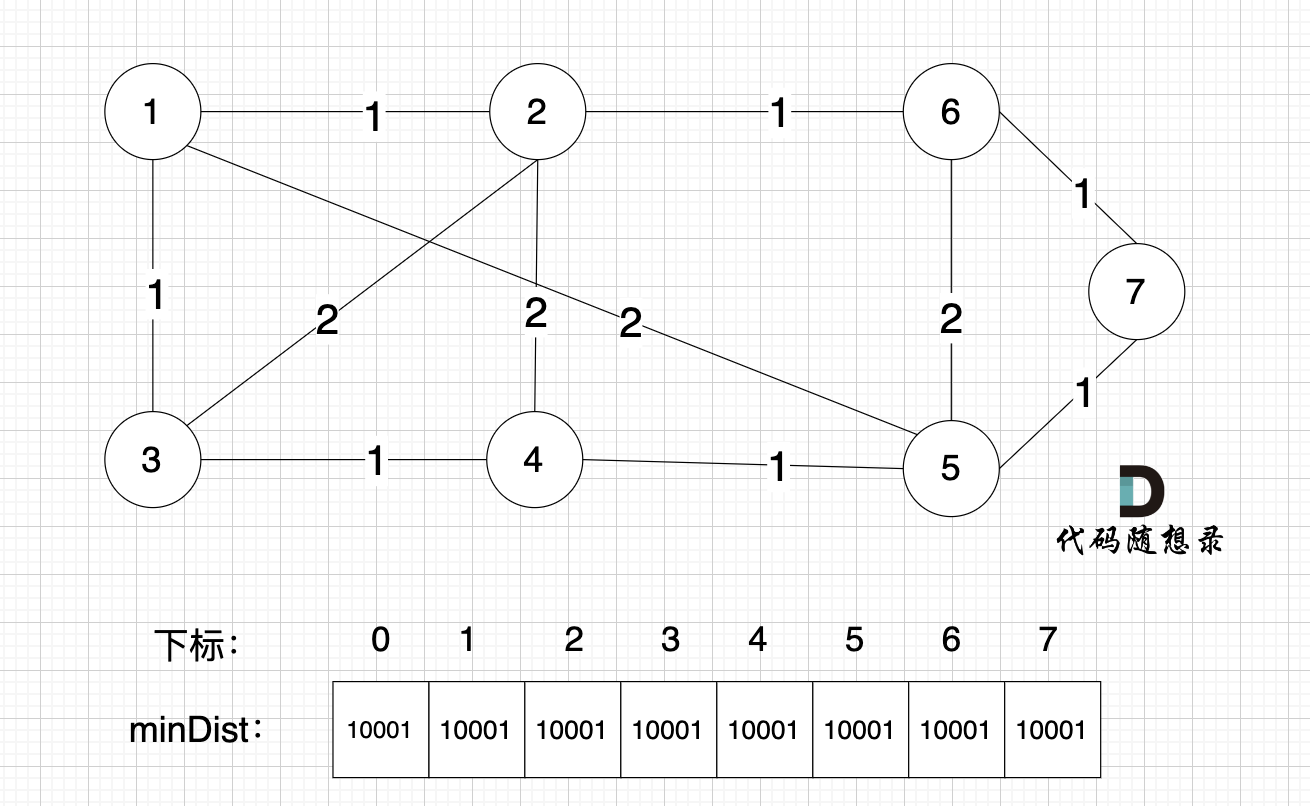
1 初始状态
minDist数组里的数值初始化为最大数,因为本题节点距离不会超过10000,所以初始化最大数为10001就可以。
相信这里录友就要问了,为什么这么做?
现在还没有最小生成树,默认每个节点距离最小生成树是最大的,这样后面我们在比较的时候,发现更近的距离,才能更新到minDist数组上。
如图:
开始构造最小生成树
2
1、prim三部曲,第一步:选距离生成树最近节点
选择距离最小生成树最近的节点,加入到最小生成树,刚开始还没有最小生成树,所以随便选一个节点加入就好(因为每一个节点一定会在最小生成树里,所以随便选一个就好),那我们选择节点1(符合遍历数组的习惯,第一个遍历的也是节点1)
2、prim三部曲,第二步:最近节点加入生成树
此时节点1已经算最小生成树的节点。
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
接下来,我们要更新所有节点距离最小生成树的距离,如图:
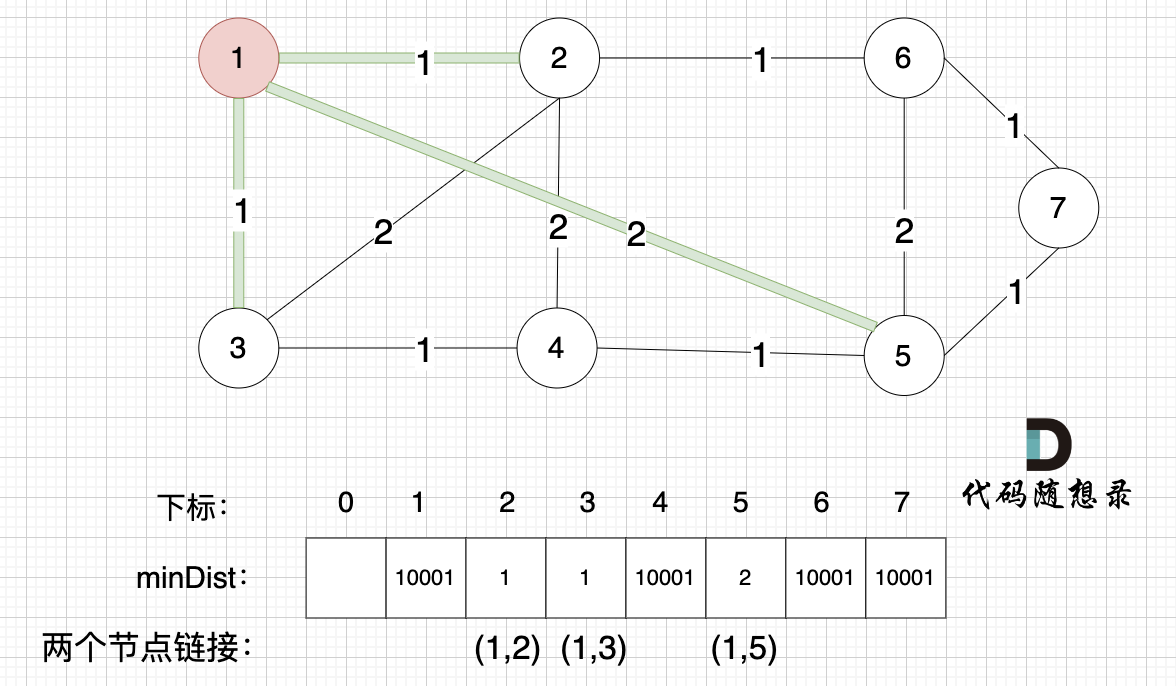
注意下标0,我们就不管它了,下标1与节点1对应,这样可以避免大家把节点搞混。
此时所有非生成树的节点距离最小生成树(节点1)的距离都已经跟新了。
- 节点2与节点1的距离为1,比原先的距离值10001小,所以更新minDist[2]。
- 节点3和节点1的距离为1,比原先的距离值10001小,所以更新minDist[3]。
- 节点5和节点1的距离为2,比原先的距离值10001小,所以更新minDist[5]。
注意图中我标记了minDist数组里更新的权值,是哪两个节点之间的权值,例如minDist[2]=1,这个1是节点1与节点2之间的连线,清楚这一点对最后我们记录最小生成树的权值总和很重要。
(我在后面依然会不断重复prim三部曲,可能基础好的录友会感觉有点啰嗦,但也是让大家感觉这三部曲求解的过程)
3
1、prim三部曲,第一步:选距离生成树最近节点
选取一个距离最小生成树(节点1)最近的非生成树里的节点,节点2,3,5距离最小生成树(节点1)最近,选节点2(其实选节点3或者节点2都可以,距离一样的)加入最小生成树。
2、prim三部曲,第二步:最近节点加入生成树
此时节点1和节点2,已经算最小生成树的节点。
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
接下来,我们要更新节点距离最小生成树的距离,如图:
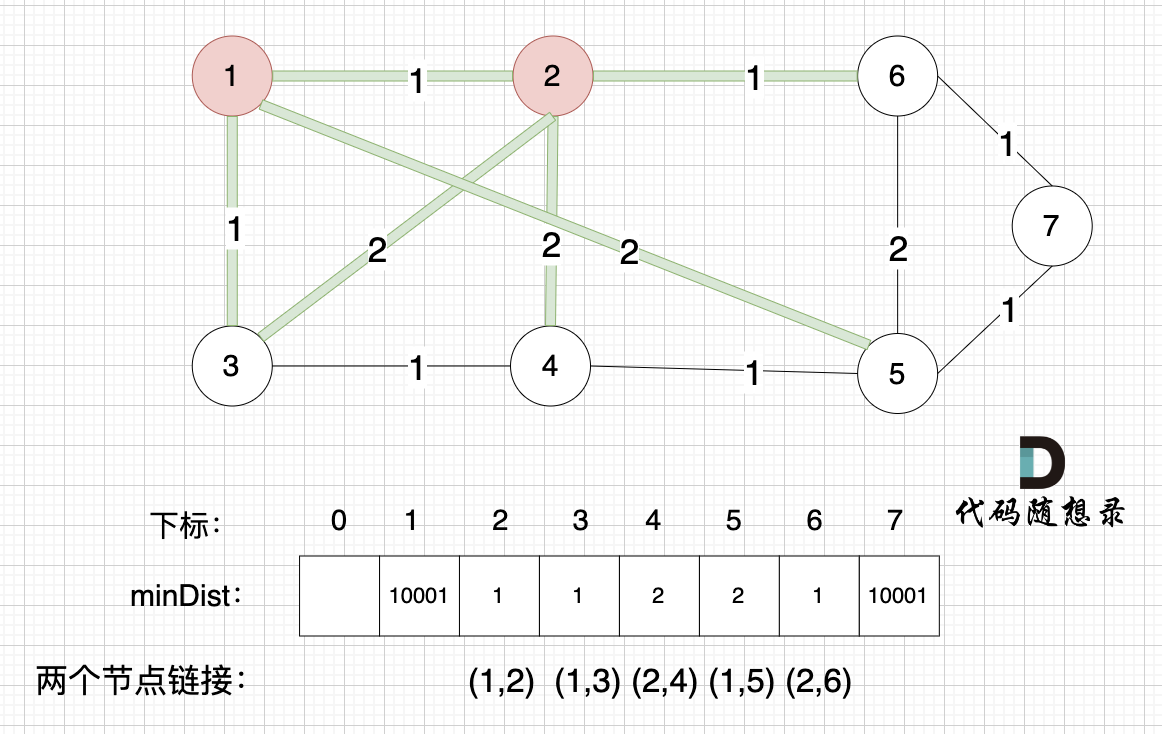
此时所有非生成树的节点距离最小生成树(节点1、节点2)的距离都已经跟新了。
- 节点3和节点2的距离为2,和原先的距离值1小,所以不用更新。
- 节点4和节点2的距离为2,比原先的距离值10001小,所以更新minDist[4]。
- 节点5和节点2的距离为10001(不连接),所以不用更新。
- 节点6和节点2的距离为1,比原先的距离值10001小,所以更新minDist[6]。
4
1、prim三部曲,第一步:选距离生成树最近节点
选择一个距离最小生成树(节点1、节点2)最近的非生成树里的节点,节点3,6距离最小生成树(节点1、节点2)最近,选节点3(选节点6也可以,距离一样)加入最小生成树。
2、prim三部曲,第二步:最近节点加入生成树
此时节点1、节点2、节点3算是最小生成树的节点。
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
接下来更新节点距离最小生成树的距离,如图:

所有非生成树的节点距离最小生成树(节点1、节点2、节点3)的距离都已经跟新了。
- 节点4和节点3的距离为1,和原先的距离值2小,所以更新minDist[4]为1。
上面为什么我们只比较节点4和节点3的距离呢?
因为节点3加入最小生成树后,非生成树节点只有节点4和节点3是链接的,所以需要重新更新一下节点4距离最小生成树的距离,其他节点距离最小生成树的距离都不变。
5
1、prim三部曲,第一步:选距离生成树最近节点
继续选择一个距离最小生成树(节点1、节点2、节点3)最近的非生成树里的节点,为了巩固大家对minDist数组的理解,这里我再啰嗦一遍:
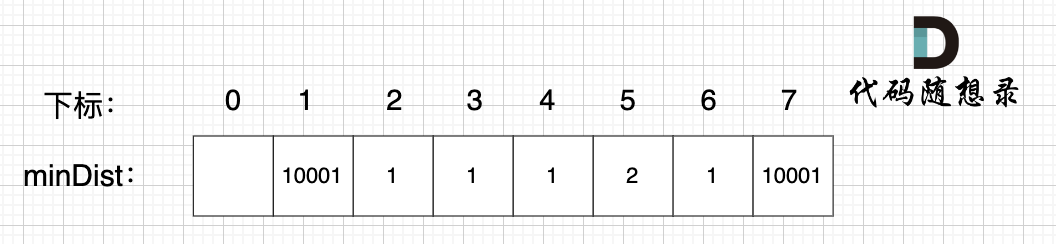
minDist数组是记录了所有非生成树节点距离生成树的最小距离,所以从数组里我们能看出来,非生成树节点4和节点6距离生成树最近。
任选一个加入生成树,我们选节点4(选节点6也行)。
注意,我们根据minDist数组,选取距离生成树最近的节点加入生成树,那么minDist数组里记录的其实也是最小生成树的边的权值(我在图中把权值对应的是哪两个节点也标记出来了)。
如果大家不理解,可以跟着我们下面的讲解,看minDist数组的变化,minDist数组里记录的权值对应的哪条边。
理解这一点很重要,因为最后我们要求最小生成树里所有边的权值和。
2、prim三部曲,第二步:最近节点加入生成树
此时节点1、节点2、节点3、节点4算是最小生成树的节点。
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
接下来更新节点距离最小生成树的距离,如图:
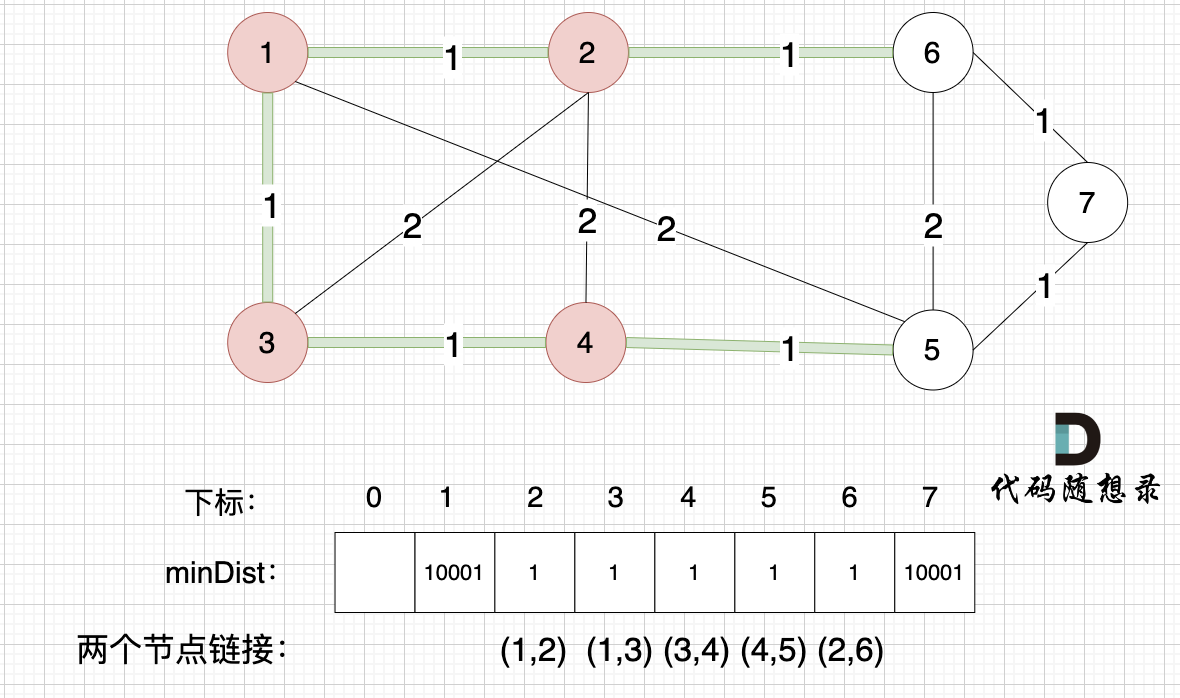
minDist数组已经更新了所有非生成树的节点距离最小生成树(节点1、节点2、节点3、节点4)的距离。
- 节点5和节点4的距离为1,和原先的距离值2小,所以更新minDist[5]为1。
6
1、prim三部曲,第一步:选距离生成树最近节点
继续选距离最小生成树(节点1、节点2、节点3、节点4)最近的非生成树里的节点,只有节点5和节点6。
选节点5(选节点6也可以)加入生成树。
2、prim三部曲,第二步:最近节点加入生成树
节点1、节点2、节点3、节点4、节点5算是最小生成树的节点。
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
接下来更新节点距离最小生成树的距离,如图:
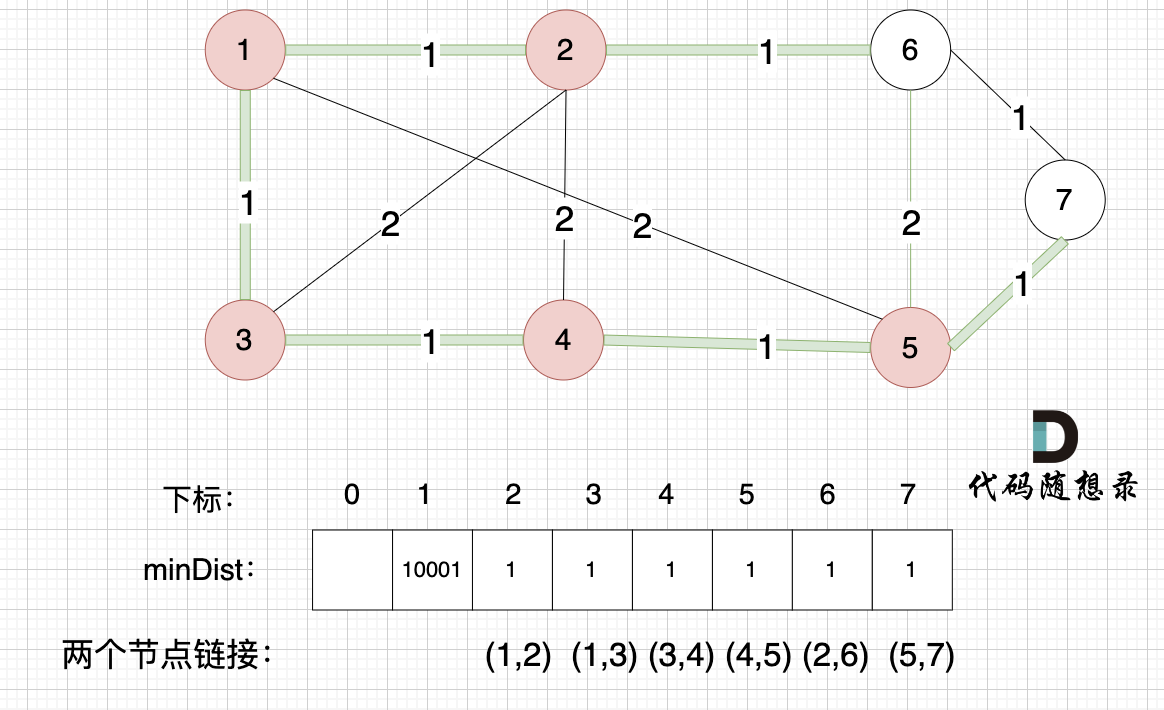
minDist数组已经更新了所有非生成树的节点距离最小生成树(节点1、节点2、节点3、节点4、节点5)的距离。
- 节点6和节点5距离为2,比原先的距离值1大,所以不更新
- 节点7和节点5距离为1,比原先的距离值10001小,更新minDist[7]
7
1、prim三部曲,第一步:选距离生成树最近节点
继续选距离最小生成树(节点1、节点2、节点3、节点4、节点5)最近的非生成树里的节点,只有节点6和节点7。
2、prim三部曲,第二步:最近节点加入生成树
选节点6(选节点7也行,距离一样的)加入生成树。
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
节点1、节点2、节点3、节点4、节点5、节点6算是最小生成树的节点,接下来更新节点距离最小生成树的距离,如图:
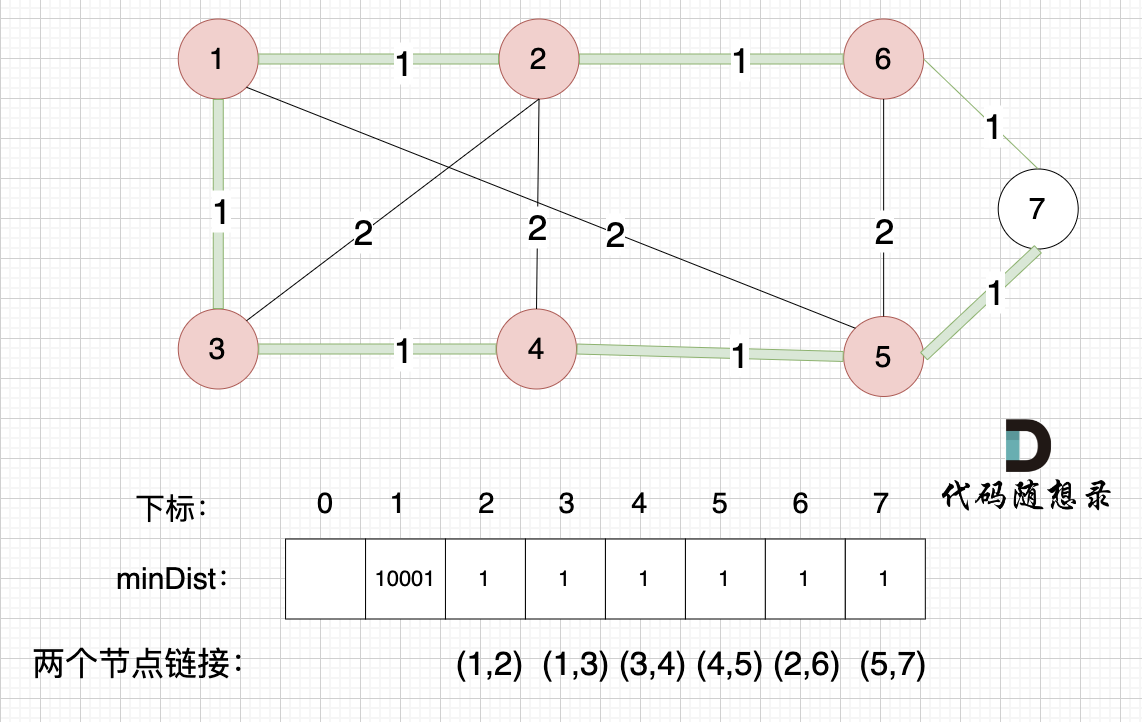
这里就不在重复描述了,大家类推,最后,节点7加入生成树,如图:
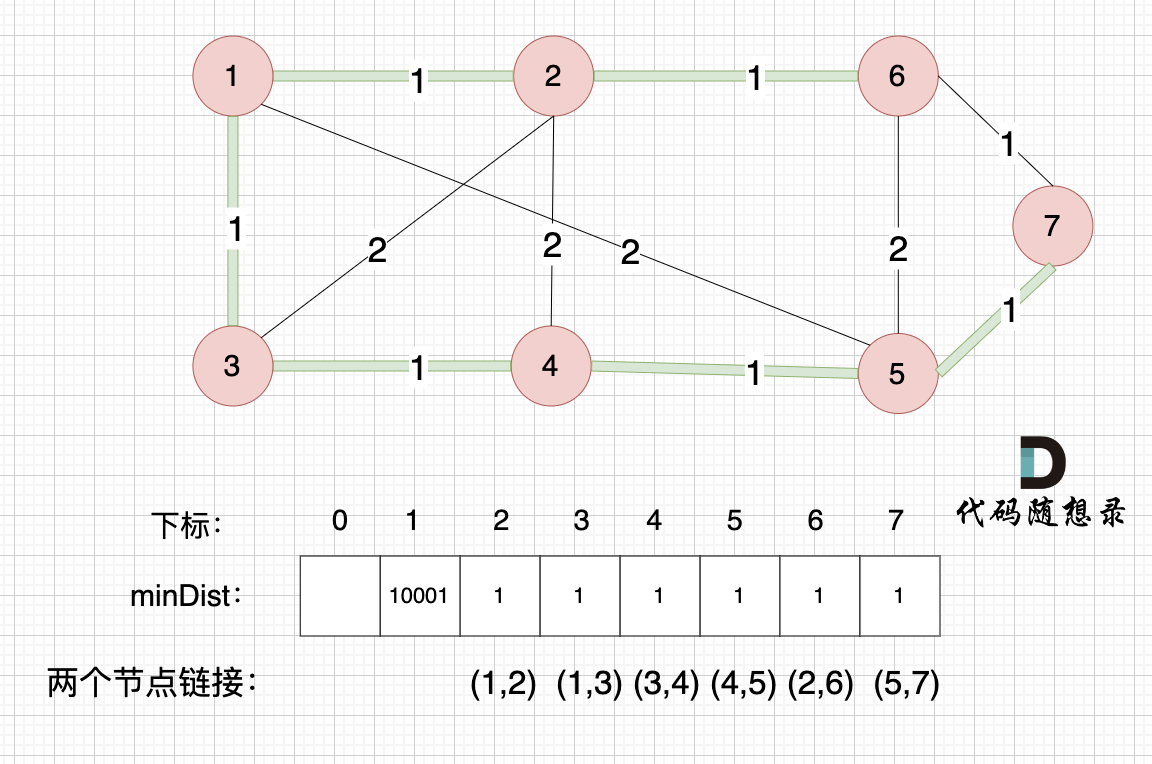
最后
最后我们就生成了一个最小生成树,绿色的边将所有节点链接到一起,并且保证权值是最小的,因为我们在更新minDist数组的时候,都是选距离最小生成树最近的点加入到树中。
讲解上面的模拟过程的时候,我已经强调多次minDist数组是记录了所有非生成树节点距离生成树的最小距离。
最后,minDist数组也就是记录的是最小生成树所有边的权值。
我在图中,特别把每条边的权值对应的是哪两个节点标记出来(例如minDist[7]=1,对应的是节点5和节点7之间的边,而不是节点6和节点7),为了就是让大家清楚,minDist里的每一个值对应的是哪条边。
那么我们要求最小生成树里边的权值总和就是把最后的minDist数组累加一起。
以下代码,我对prim三部曲,做了重点注释,大家根据这三步,就可以透彻理解prim。
#include<iostream>
#include<vector>
#include <climits>
using namespace std;
int main() {
int v, e;
int x, y, k;
cin >> v >> e;
// 填一个默认最大值,题目描述val最大为10000
vector<vector<int>> grid(v + 1, vector<int>(v + 1, 10001));
while (e--) {
cin >> x >> y >> k;
// 因为是双向图,所以两个方向都要填上
grid[x][y] = k;
grid[y][x] = k;
}
// 所有节点到最小生成树的最小距离
vector<int> minDist(v + 1, 10001);
// 这个节点是否在树里
vector<bool> isInTree(v + 1, false);
// 我们只需要循环 n-1次,建立 n - 1条边,就可以把n个节点的图连在一起
for (int i = 1; i < v; i++) {
// 1、prim三部曲,第一步:选距离生成树最近节点
int cur = -1; // 选中哪个节点 加入最小生成树
int minVal = INT_MAX;
for (int j = 1; j <= v; j++) { // 1 - v,顶点编号,这里下标从1开始
// 选取最小生成树节点的条件:
// (1)不在最小生成树里
// (2)距离最小生成树最近的节点
if (!isInTree[j] && minDist[j] < minVal) {
minVal = minDist[j];
cur = j;
}
}
// 2、prim三部曲,第二步:最近节点(cur)加入生成树
isInTree[cur] = true;
// 3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
// cur节点加入之后, 最小生成树加入了新的节点,那么所有节点到 最小生成树的距离(即minDist数组)需要更新一下
// 由于cur节点是新加入到最小生成树,那么只需要关心与 cur 相连的 非生成树节点 的距离 是否比 原来 非生成树节点到生成树节点的距离更小了呢
for (int j = 1; j <= v; j++) {
// 更新的条件:
// (1)节点是 非生成树里的节点
// (2)与cur相连的某节点的权值 比 该某节点距离最小生成树的距离小
// 很多录友看到自己 就想不明白什么意思,其实就是 cur 是新加入 最小生成树的节点,那么 所有非生成树的节点距离生成树节点的最近距离 由于 cur的新加入,需要更新一下数据了
if (!isInTree[j] && grid[cur][j] < minDist[j]) {
minDist[j] = grid[cur][j];
}
}
}
// 统计结果
int result = 0;
for (int i = 2; i <= v; i++) { // 不计第一个顶点,因为统计的是边的权值,v个节点有 v-1条边
result += minDist[i];
}
cout << result << endl;
}
时间复杂度为O(n^2),其中n为节点数量。
拓展
上面讲解的是记录了最小生成树所有边的权值,如果让打印出来最小生成树的每条边呢?或者说要把这个最小生成树画出来呢?
此时我们就需要把最小生成树里每一条边记录下来。
此时有两个问题:
- 1、用什么结构来记录
- 2、如何记录
如果记录边,其实就是记录两个节点就可以,两个节点连成一条边。
如何记录两个节点呢?
我们使用一维数组就可以记录。parent[节点编号] = 节点编号,这样就把一条边记录下来了。(当然如果节点编号非常大,可以考虑使用map)
使用一维数组记录是有向边,不过我们这里不需要记录方向,所以只关注两条边是连接的就行。
parent数组初始化代码:
vector<int> parent(v + 1, -1);接下来就是第二个问题,如何记录?
我们再来回顾一下prim三部曲,
- 第一步,选距离生成树最近节点
- 第二步,最近节点加入生成树
- 第三步,更新非生成树节点到生成树的距离(即更新minDist数组)
大家先思考一下,我们是在第几步,可以记录最小生成树的边呢?
在本面上半篇我们讲解过:“我们根据minDist数组,选组距离生成树最近的节点加入生成树,那么minDist数组里记录的其实也是最小生成树的边的权值。”
既然minDist数组记录了最小生成树的边,是不是就是在更新minDist数组的时候,去更新parent数组来记录一下对应的边呢。
所以在prim三部曲中的第三步,更新parent数组,代码如下:
for (int j = 1; j <= v; j++) {
if (!isInTree[j] && grid[cur][j] < minDist[j]) {
minDist[j] = grid[cur][j];
parent[j] = cur; // 记录最小生成树的边 (注意数组指向的顺序很重要)
}
}代码中注释中,我强调了数组指向的顺序很重要。因为不少录友在这里会写成这样: parent[cur] = j 。
这里估计大家会疑惑了,parent[节点编号A] = 节点编号B,就表示A和B相连,我们这里就不用在意方向,代码中为什么只能 parent[j] = cur 而不能 parent[cur] = j 这么写呢?
如果写成 parent[cur] = j,在for循环中,有多个j满足要求,那么 parent[cur] 就会被反复覆盖,因为cur是一个固定值。
举个例子,cur=1,在for循环中,可能就j=2,j=3,j=4都符合条件,那么本来应该记录节点1与节点2、节点3、节点4相连的。
如果 parent[cur] = j 这么写,最后更新的逻辑是 parent[1] = 2, parent[1] = 3, parent[1] = 4,最后只能记录节点1与节点4相连,其他相连情况都被覆盖了。
如果这么写 parent[j] = cur,那就是 parent[2] = 1, parent[3] = 1, parent[4] = 1 ,这样才能完整表示出节点1与其他节点都是链接的,才没有被覆盖。
主要问题也是我们使用了一维数组来记录。
如果是二维数组,来记录两个点链接,例如 parent[节点编号A][节点编号B] = 1 ,parent[节点编号B][节点编号A] = 1,来表示节点A与节点B相连,那就没有上面说的这个注意事项了,当然这么做的话,就是多开辟的内存空间。
以下是输出最小生成树边的代码,不算最后输出,就额外添加了两行代码,我都注释标记了:
#include<iostream>
#include<vector>
#include <climits>
using namespace std;
int main() {
int v, e;
int x, y, k;
cin >> v >> e;
vector<vector<int>> grid(v + 1, vector<int>(v + 1, 10001));
while (e--) {
cin >> x >> y >> k;
grid[x][y] = k;
grid[y][x] = k;
}
vector<int> minDist(v + 1, 10001);
vector<bool> isInTree(v + 1, false);
//加上初始化
vector<int> parent(v + 1, -1);
for (int i = 1; i < v; i++) {
int cur = -1;
int minVal = INT_MAX;
for (int j = 1; j <= v; j++) {
if (!isInTree[j] && minDist[j] < minVal) {
minVal = minDist[j];
cur = j;
}
}
isInTree[cur] = true;
for (int j = 1; j <= v; j++) {
if (!isInTree[j] && grid[cur][j] < minDist[j]) {
minDist[j] = grid[cur][j];
parent[j] = cur; // 记录边
}
}
}
// 输出 最小生成树边的链接情况
for (int i = 1; i <= v; i++) {
cout << i << "->" << parent[i] << endl;
}
}
按照本题示例,代码输入如下:
1->-1
2->1
3->1
4->3
5->4
6->2
7->5
注意,这里是无向图,我在输出上添加了箭头仅仅是为了方便大家看出是边的意思。
大家可以和我们本题最后生成的最小生成树的图去对比一下边的链接情况:
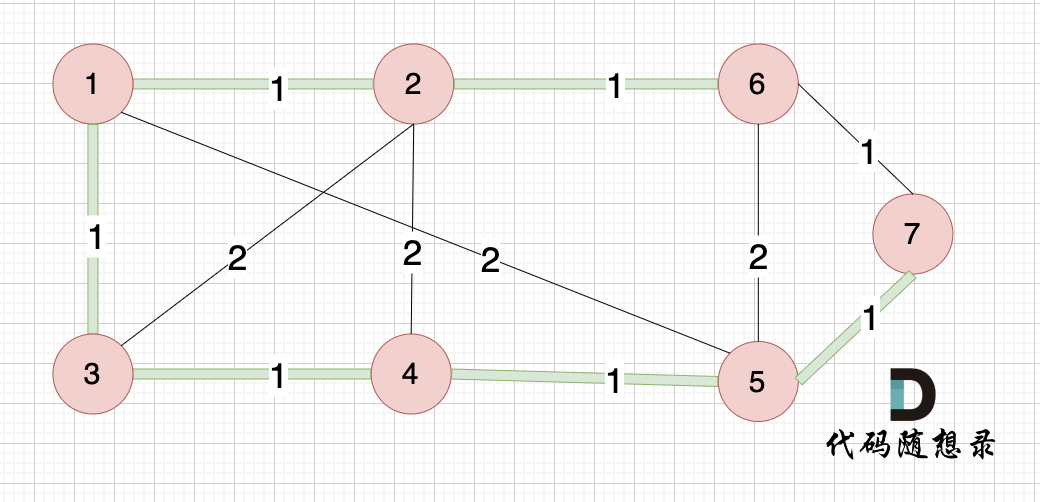
绿色的边是最小生成树,和我们的输出完全一致。
总结
此时我就把prim算法讲解完毕了,我们再来回顾一下。
关于prim算法,我自创了三部曲,来帮助大家理解:
- 第一步,选距离生成树最近节点
- 第二步,最近节点加入生成树
- 第三步,更新非生成树节点到生成树的距离(即更新minDist数组)
大家只要理解这三部曲,prim算法至少是可以写出一个框架出来,然后在慢慢补充细节,这样不至于自己在写prim的时候两眼一抹黑完全凭感觉去写。 这也为什么很多录友感觉prim算法比较难,而且每次学会来,隔一段时间又不会写了,主要是没有一个纲领。
理解这三部曲之后,更重要的就是理解minDist数组。
minDist数组是prim算法的灵魂,它帮助prim算法完成最重要的一步,就是如何找到距离最小生成树最近的点。
再来帮大家回顾minDist数组的含义:记录每一个节点距离最小生成树的最近距离。
理解minDist数组,至少大家看prim算法的代码不会懵。
也正是因为minDist数组的作用,我们根据minDist数组,选取距离生成树最近的节点加入生成树,那么minDist数组里记录的其实也是最小生成树的边的权值。
所以我们求最小生成树的权值和就是计算后的minDist数组数值总和。
最后我们拓展了如何获得最小生成树的每一条边,其实添加的代码很简单,主要是理解为什么使用parent数组来记录边以及在哪里更新parent数组。
同时,因为使用一维数组,数组的下标和数组如何赋值很重要,不要搞反,导致结果被覆盖。
好了,以上为总结,录友们学习愉快。
其他语言版本
Java
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int v = scanner.nextInt();
int e = scanner.nextInt();
// 初始化邻接矩阵,所有值初始化为一个大值,表示无穷大
int[][] grid = new int[v + 1][v + 1];
for (int i = 0; i <= v; i++) {
Arrays.fill(grid[i], 10001);
}
// 读取边的信息并填充邻接矩阵
for (int i = 0; i < e; i++) {
int x = scanner.nextInt();
int y = scanner.nextInt();
int k = scanner.nextInt();
grid[x][y] = k;
grid[y][x] = k;
}
// 所有节点到最小生成树的最小距离
int[] minDist = new int[v + 1];
Arrays.fill(minDist, 10001);
// 记录节点是否在树里
boolean[] isInTree = new boolean[v + 1];
// Prim算法主循环
for (int i = 1; i < v; i++) {
int cur = -1;
int minVal = Integer.MAX_VALUE;
// 选择距离生成树最近的节点
for (int j = 1; j <= v; j++) {
if (!isInTree[j] && minDist[j] < minVal) {
minVal = minDist[j];
cur = j;
}
}
// 将最近的节点加入生成树
isInTree[cur] = true;
// 更新非生成树节点到生成树的距离
for (int j = 1; j <= v; j++) {
if (!isInTree[j] && grid[cur][j] < minDist[j]) {
minDist[j] = grid[cur][j];
}
}
}
// 统计结果
int result = 0;
for (int i = 2; i <= v; i++) {
result += minDist[i];
}
System.out.println(result);
scanner.close();
}
}
Python
# 接收输入
v, e = list(map(int, input().strip().split()))
# 按照常规的邻接矩阵存储图信息,不可达的初始化为10001
graph = [[10001] * (v+1) for _ in range(v+1)]
for _ in range(e):
x, y, w = list(map(int, input().strip().split()))
graph[x][y] = w
graph[y][x] = w
# 定义加入生成树的标记数组和未加入生成树的最近距离
visited = [False] * (v + 1)
minDist = [10001] * (v + 1)
# 循环 n - 1 次,建立 n - 1 条边
# 从节点视角来看:每次选中一个节点加入树,更新剩余的节点到树的最短距离,
# 这一步其实蕴含了确定下一条选取的边,计入总路程 ans 的计算
for _ in range(1, v + 1):
min_val = 10002
cur = -1
for j in range(1, v + 1):
if visited[j] == False and minDist[j] < min_val:
cur = j
min_val = minDist[j]
visited[cur] = True
for j in range(1, v + 1):
if visited[j] == False and minDist[j] > graph[cur][j]:
minDist[j] = graph[cur][j]
ans = 0
for i in range(2, v + 1):
ans += minDist[i]
print(ans)def prim(v, e, edges):
import sys
import heapq
# 初始化邻接矩阵,所有值初始化为一个大值,表示无穷大
grid = [[10001] * (v + 1) for _ in range(v + 1)]
# 读取边的信息并填充邻接矩阵
for edge in edges:
x, y, k = edge
grid[x][y] = k
grid[y][x] = k
# 所有节点到最小生成树的最小距离
minDist = [10001] * (v + 1)
# 记录节点是否在树里
isInTree = [False] * (v + 1)
# Prim算法主循环
for i in range(1, v):
cur = -1
minVal = sys.maxsize
# 选择距离生成树最近的节点
for j in range(1, v + 1):
if not isInTree[j] and minDist[j] < minVal:
minVal = minDist[j]
cur = j
# 将最近的节点加入生成树
isInTree[cur] = True
# 更新非生成树节点到生成树的距离
for j in range(1, v + 1):
if not isInTree[j] and grid[cur][j] < minDist[j]:
minDist[j] = grid[cur][j]
# 统计结果
result = sum(minDist[2:v+1])
return result
if __name__ == "__main__":
import sys
input = sys.stdin.read
data = input().split()
v = int(data[0])
e = int(data[1])
edges = []
index = 2
for _ in range(e):
x = int(data[index])
y = int(data[index + 1])
k = int(data[index + 2])
edges.append((x, y, k))
index += 3
result = prim(v, e, edges)
print(result)
Go
Rust
JavaScript
function prim(v, edges) {
const grid = Array.from({ length: v + 1 }, () => new Array(v + 1).fill(10001)); // Fixed grid initialization
const minDist = new Array(v + 1).fill(10001)
const isInTree = new Array(v + 1).fill(false)
// 建構鄰接矩陣
for(const [v1, v2, w] of edges) {
grid[v1][v2] = w
grid[v2][v1] = w
}
// prim 演算法
for (let i = 1 ; i < v ; i++) {
let cur = -1
let tempMinDist = Number.MAX_VALUE
// 1. 尋找距離生成樹最近的節點
for (let j = 1 ; j < v + 1 ; j++) {
if (!isInTree[j] && minDist[j] < tempMinDist) {
tempMinDist = minDist[j]
cur = j
}
}
// 2. 將節點放入生成樹
isInTree[cur] = true
// 3. 更新非生成樹節點與生成樹的最短距離
for (let j = 1 ; j < v + 1 ; j++) {
if (!isInTree[j] && grid[cur][j] < minDist[j]) {
minDist[j] = grid[cur][j]
}
}
}
console.log(minDist.slice(2).reduce((acc, cur) => acc + cur, 0))
}
async function main() {
const rl = require('readline').createInterface({ input: process.stdin })
const iter = rl[Symbol.asyncIterator]()
const readline = async () => (await iter.next()).value
const [v, e] = (await readline()).split(" ").map(Number)
const edges = []
for (let i = 0 ; i < e ; i++) {
edges.push((await readline()).split(" ").map(Number))
}
prim(v, edges)
}
main()