743.网络延迟时间
https://leetcode.cn/problems/network-delay-time/description/
有 n 个网络节点,标记为 1 到 n。
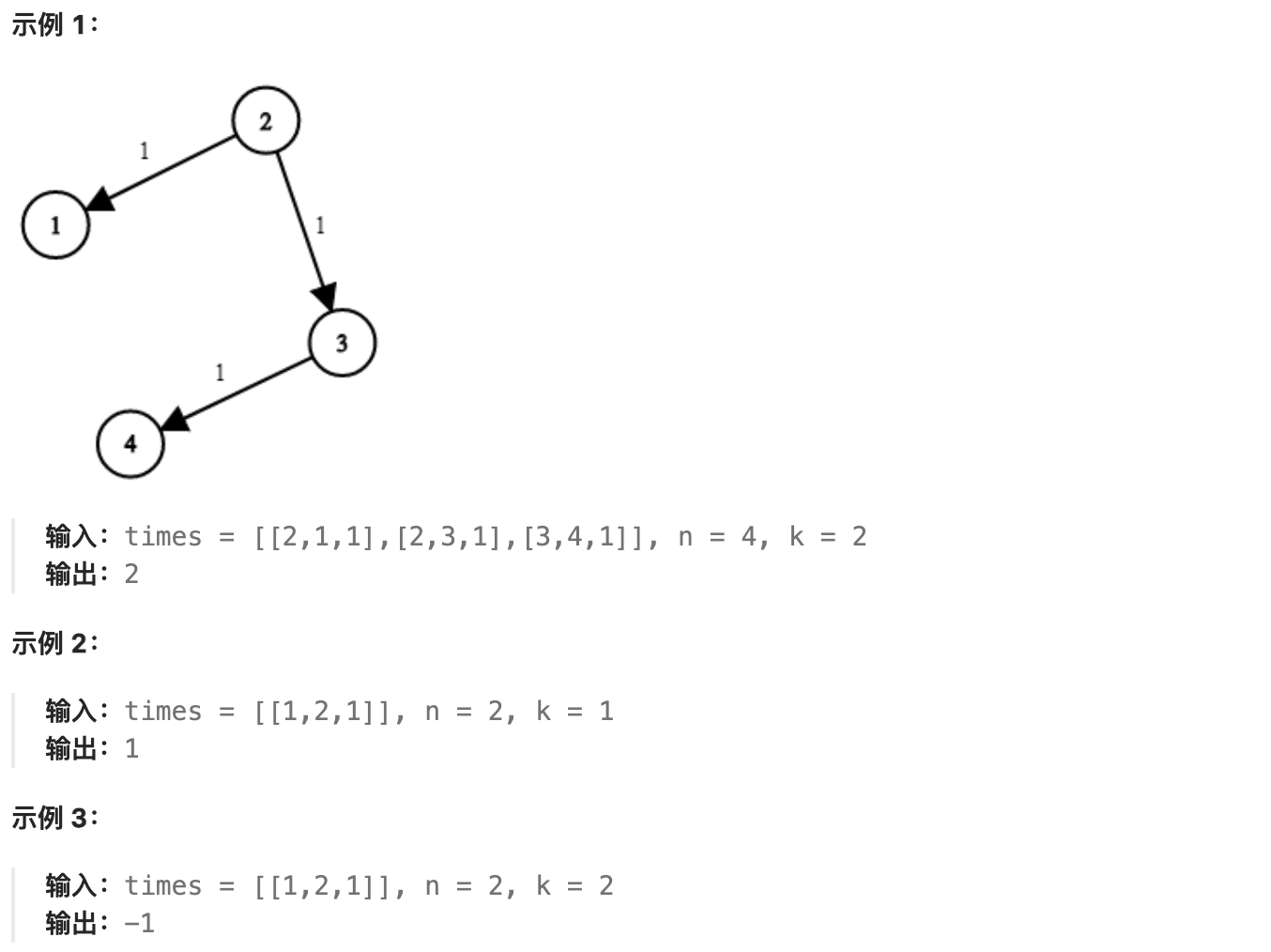
给你一个列表 times,表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi),其中 ui 是源节点,vi 是目标节点, wi 是一个信号从源节点传递到目标节点的时间。
现在,从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号?如果不能使所有节点收到信号,返回 -1 。
提示:
- 1 <= k <= n <= 100
- 1 <= times.length <= 6000
- times[i].length == 3
- 1 <= ui, vi <= n
- ui != vi
- 0 <= wi <= 100
- 所有 (ui, vi) 对都 互不相同(即,不含重复边)
dijkstra 精讲
本题就是求最短路,最短路是图论中的经典问题即:给出一个有向图,一个起点,一个终点,问起点到终点的最短路径。
接下来,我们来详细讲解最短路算法中的 dijkstra 算法。
dijkstra算法:在有权图(权值非负数)中求从起点到其他节点的最短路径算法。
需要注意两点:
- dijkstra 算法可以同时求 起点到所有节点的最短路径
- 权值不能为负数
(这两点后面我们会讲到)
如本题示例中的图:
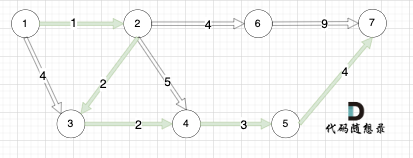
起点(节点1)到终点(节点7) 的最短路径是 图中 标记绿线的部分。
最短路径的权值为12。
其实 dijkstra 算法 和 我们之前讲解的prim算法思路非常接近,如果大家认真学过prim算法,那么理解 Dijkstra 算法会相对容易很多。(这也是我要先讲prim再讲dijkstra的原因)
dijkstra 算法 同样是贪心的思路,不断寻找距离 源点最近的没有访问过的节点。
这里我也给出 dijkstra三部曲:
- 第一步,选源点到哪个节点近且该节点未被访问过
- 第二步,该最近节点被标记访问过
- 第三步,更新非访问节点到源点的距离(即更新minDist数组)
大家此时已经会发现,这和prim算法 怎么这么像呢。
我在prim算法讲解中也给出了三部曲。 prim 和 dijkstra 确实很像,思路也是类似的,这一点我在后面还会详细来讲。
在dijkstra算法中,同样有一个数组很重要,起名为:minDist。
minDist数组 用来记录 每一个节点距离源点的最小距离。
理解这一点很重要,也是理解 dijkstra 算法的核心所在。
大家现在看着可能有点懵,不知道什么意思。
没关系,先让大家有一个印象,对理解后面讲解有帮助。
我们先来画图看一下 dijkstra 的工作过程,以本题示例为例: (以下为朴素版dijkstra的思路)
(示例中节点编号是从1开始,所以为了让大家看的不晕,minDist数组下标我也从 1 开始计数,下标0 就不使用了,这样 下标和节点标号就可以对应上了,避免大家搞混)
朴素版dijkstra
模拟过程
0、初始化
minDist数组数值初始化为int最大值。
这里在强点一下 minDist数组的含义:记录所有节点到源点的最短路径,那么初始化的时候就应该初始为最大值,这样才能在后续出现最短路径的时候及时更新。

(图中,max 表示默认值,节点0 不做处理,统一从下标1 开始计算,这样下标和节点数值统一, 方便大家理解,避免搞混)
源点(节点1) 到自己的距离为0,所以 minDist[1] = 0
此时所有节点都没有被访问过,所以 visited数组都为0
以下为dijkstra 三部曲
1、选源点到哪个节点近且该节点未被访问过
源点距离源点最近,距离为0,且未被访问。
2、该最近节点被标记访问过
标记源点访问过
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:

更新 minDist数组,即:源点(节点1) 到 节点2 和 节点3的距离。
- 源点到节点2的最短距离为1,小于原minDist[2]的数值max,更新minDist[2] = 1
- 源点到节点3的最短距离为4,小于原minDist[3]的数值max,更新minDist[4] = 4
可能有录友问:为啥和 minDist[2] 比较?
再强调一下 minDist[2] 的含义,它表示源点到节点2的最短距离,那么目前我们得到了 源点到节点2的最短距离为1,小于默认值max,所以更新。 minDist[3]的更新同理
1、选源点到哪个节点近且该节点未被访问过
未访问过的节点中,源点到节点2距离最近,选节点2
2、该最近节点被标记访问过
节点2被标记访问过
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
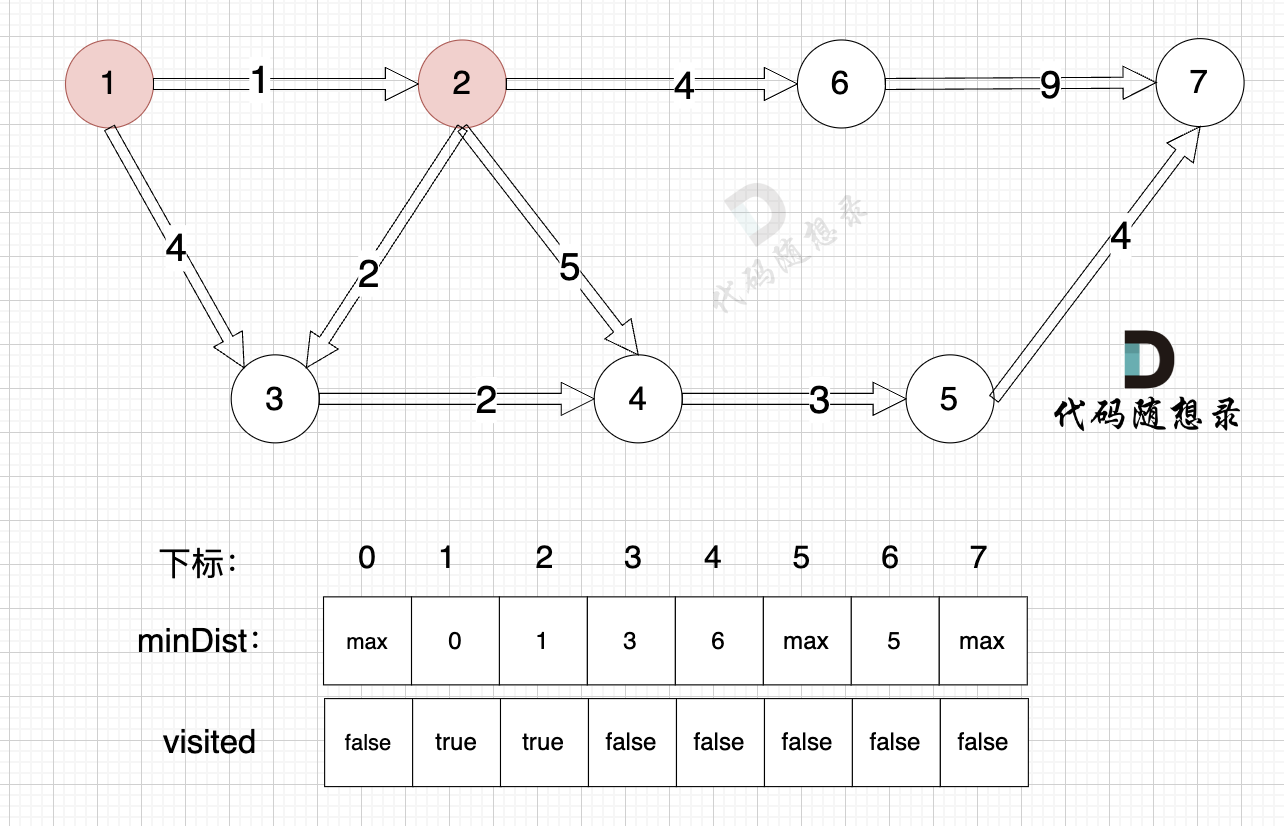
更新 minDist数组,即:源点(节点1) 到 节点6 、 节点3 和 节点4的距离。
为什么更新这些节点呢? 怎么不更新其他节点呢?
因为 源点(节点1)通过 已经计算过的节点(节点2) 可以链接到的节点 有 节点3,节点4和节点6.
更新 minDist数组:
- 源点到节点6的最短距离为5,小于原minDist[6]的数值max,更新minDist[6] = 5
- 源点到节点3的最短距离为3,小于原minDist[3]的数值4,更新minDist[3] = 3
- 源点到节点4的最短距离为6,小于原minDist[4]的数值max,更新minDist[4] = 6
1、选源点到哪个节点近且该节点未被访问过
未访问过的节点中,源点距离哪些节点最近,怎么算的?
其实就是看 minDist数组里的数值,minDist 记录了 源点到所有节点的最近距离,结合visited数组筛选出未访问的节点就好。
从 上面的图,或者 从minDist数组中,我们都能看出 未访问过的节点中,源点(节点1)到节点3距离最近。
2、该最近节点被标记访问过
节点3被标记访问过
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:

由于节点3的加入,那么源点可以有新的路径链接到节点4 所以更新minDist数组:
更新 minDist数组:
- 源点到节点4的最短距离为5,小于原minDist[4]的数值6,更新minDist[4] = 5
1、选源点到哪个节点近且该节点未被访问过
距离源点最近且没有被访问过的节点,有节点4 和 节点6,距离源点距离都是 5 (minDist[4] = 5,minDist[6] = 5) ,选哪个节点都可以。
2、该最近节点被标记访问过
节点4被标记访问过
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
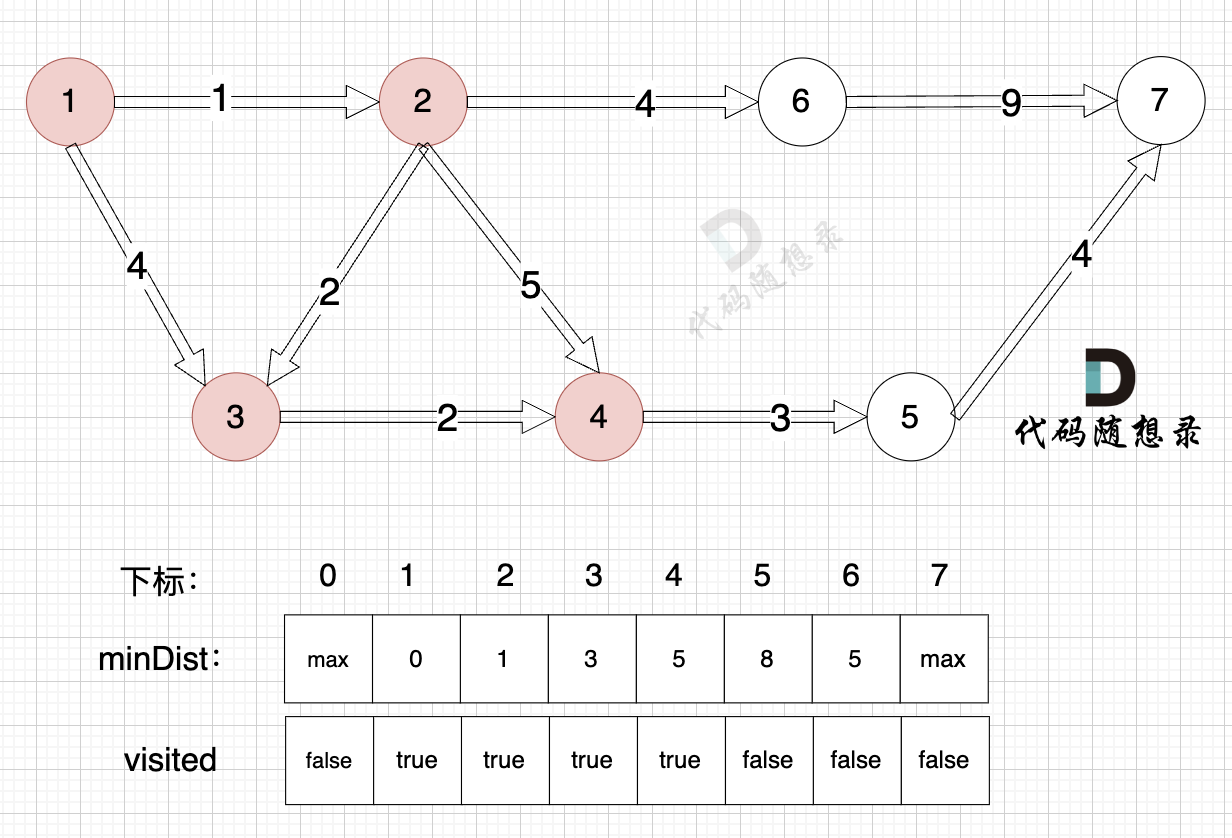
由于节点4的加入,那么源点可以链接到节点5 所以更新minDist数组:
- 源点到节点5的最短距离为8,小于原minDist[5]的数值max,更新minDist[5] = 8
1、选源点到哪个节点近且该节点未被访问过
距离源点最近且没有被访问过的节点,是节点6,距离源点距离是 5 (minDist[6] = 5)
2、该最近节点被标记访问过
节点6 被标记访问过
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
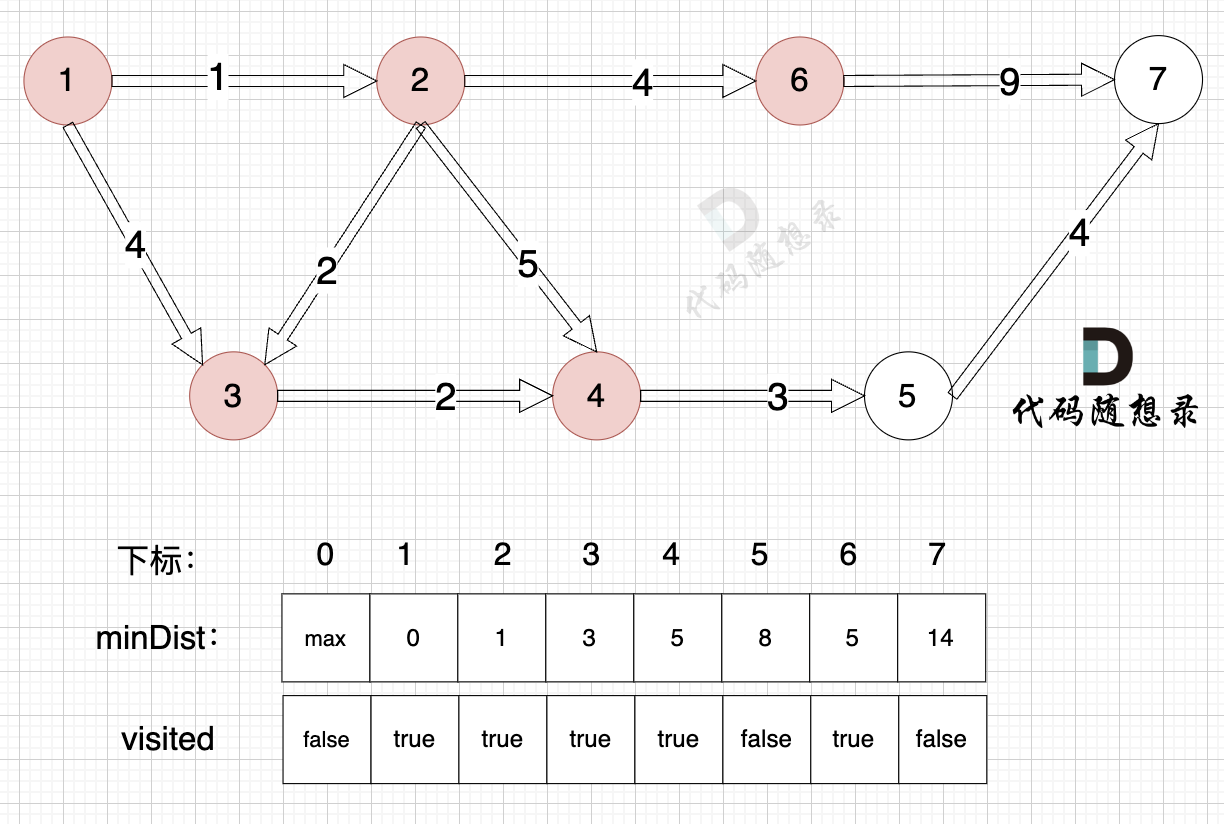
由于节点6的加入,那么源点可以链接到节点7 所以 更新minDist数组:
- 源点到节点7的最短距离为14,小于原minDist[7]的数值max,更新minDist[7] = 14
1、选源点到哪个节点近且该节点未被访问过
距离源点最近且没有被访问过的节点,是节点5,距离源点距离是 8 (minDist[5] = 8)
2、该最近节点被标记访问过
节点5 被标记访问过
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
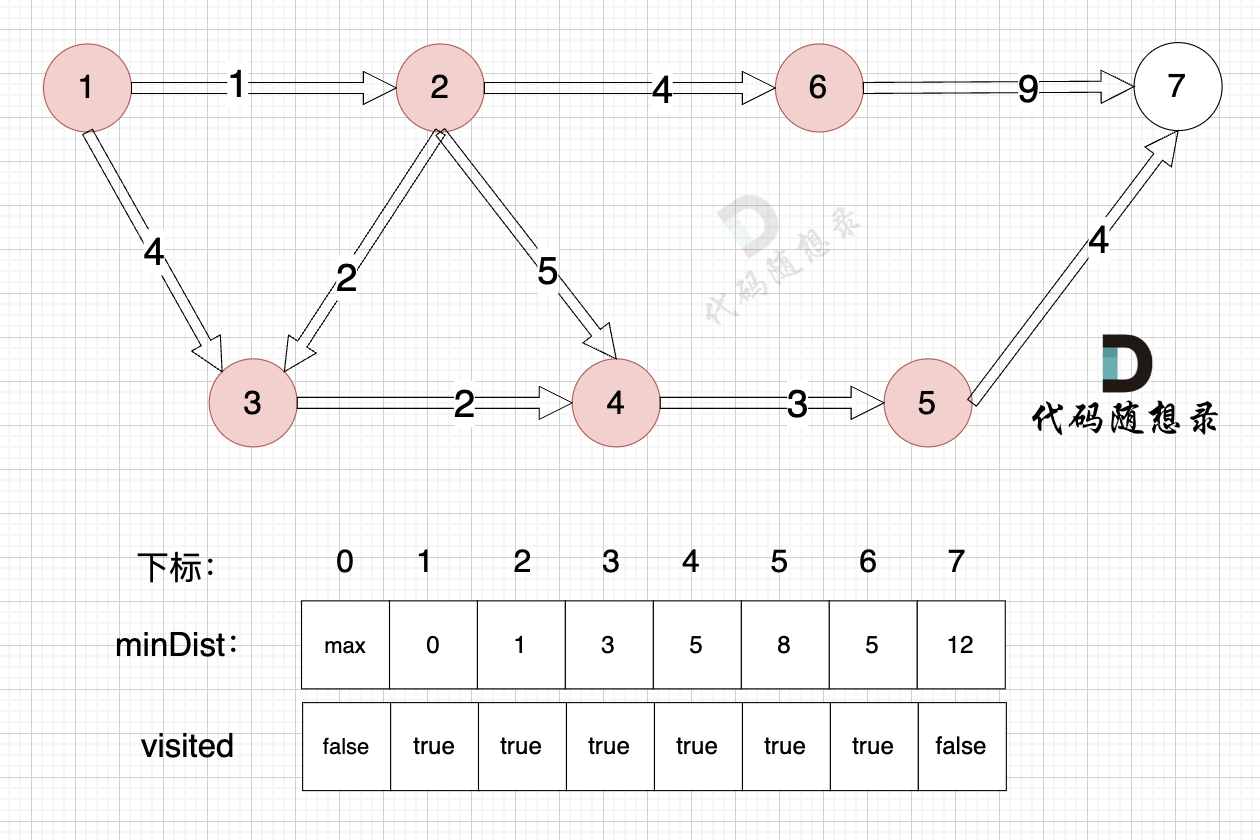
由于节点5的加入,那么源点有新的路径可以链接到节点7 所以 更新minDist数组:
- 源点到节点7的最短距离为12,小于原minDist[7]的数值14,更新minDist[7] = 12
1、选源点到哪个节点近且该节点未被访问过
距离源点最近且没有被访问过的节点,是节点7(终点),距离源点距离是 12 (minDist[7] = 12)
2、该最近节点被标记访问过
节点7 被标记访问过
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
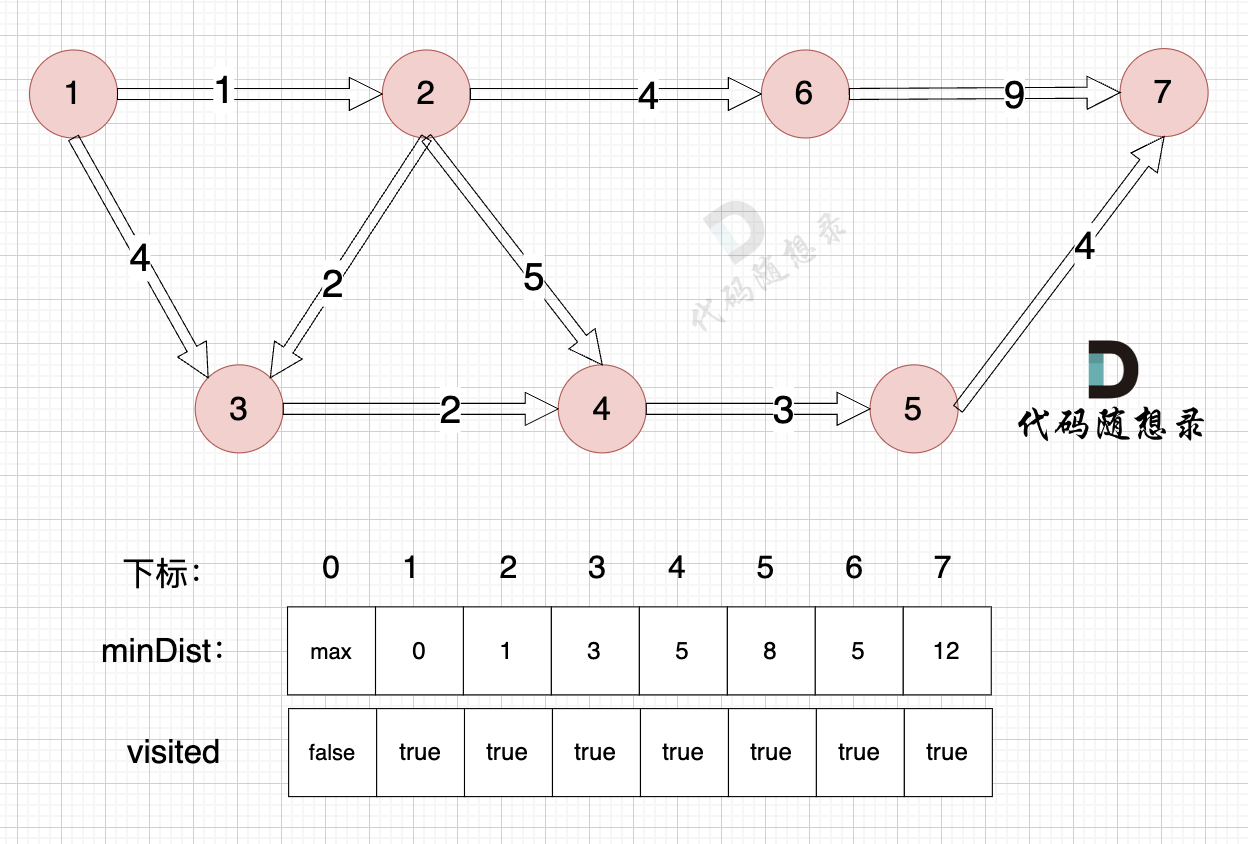
节点7加入,但节点7到节点7的距离为0,所以 不用更新minDist数组
最后我们要求起点(节点1) 到终点 (节点7)的距离。
再来回顾一下minDist数组的含义:记录 每一个节点距离源点的最小距离。
那么起到(节点1)到终点(节点7)的最短距离就是 minDist[7] ,按上面举例讲解来说,minDist[7] = 12,节点1 到节点7的最短路径为 12。
路径如图:
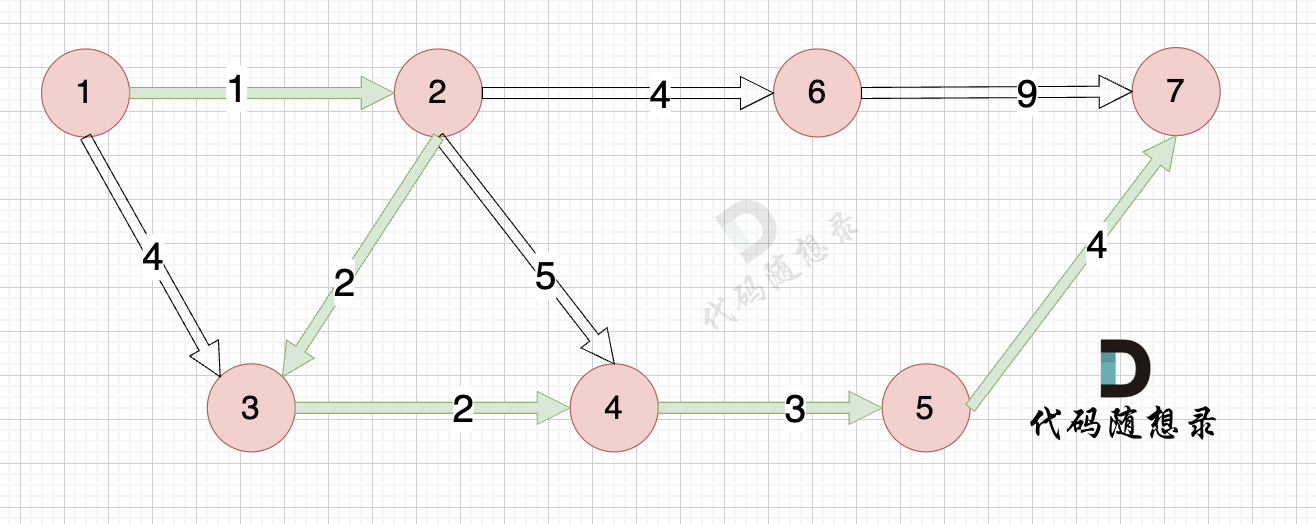
在上面的讲解中,每一步 我都是按照 dijkstra 三部曲来讲解的,理解了这三部曲,代码也就好懂的。
代码实现
本题代码如下,里面的 三部曲 我都做了注释,大家按照我上面的讲解 来看如下代码:
class Solution {
public:
int networkDelayTime(vector<vector<int>>& times, int n, int k) {
// 注意题目中给的二维数组并不是领接矩阵
// 需要邻接矩阵来存图
// 因为本题处理方式是节点标号从1开始,所以数组的大小都是 n+1
vector<vector<int>> grid(n + 1, vector<int>(n + 1, INT_MAX));
for(int i = 0; i < times.size(); i++){
int p1 = times[i][0];
int p2 = times[i][1];
grid[p1][p2] = times[i][2];
}
// 存储从源点到每个节点的最短距离
std::vector<int> minDist(n + 1, INT_MAX);
// 记录顶点是否被访问过
std::vector<bool> visited(n + 1, false);
minDist[k] = 0; // 起始点到自身的距离为0
for (int i = 1; i <= n; i++) {
int minVal = INT_MAX;
int cur = 1;
// 遍历每个节点,选择未被访问的节点集合中哪个节点到源点的距离最小
for (int v = 1; v <= n; ++v) {
if (!visited[v] && minDist[v] <= minVal) {
minVal = minDist[v];
cur = v;
}
}
visited[cur] = true; // 标记该顶点已被访问
for (int v = 1; v <= n; v++) {
if (!visited[v] && grid[cur][v] != INT_MAX && minDist[cur] + grid[cur][v] < minDist[v]) {
minDist[v] = minDist[cur] + grid[cur][v];
}
}
}
// 源点到最远的节点的时间,也就是寻找 源点到所有节点最短路径的最大值
int result = 0;
for (int i = 1; i <= n; i++) {
if (minDist[i] == INT_MAX) return -1;// 没有路径
result = max(minDist[i], result);
}
return result;
}
};- 时间复杂度:O(n^2)
- 空间复杂度:O(n^2)
debug方法
写这种题目难免会有各种各样的问题,我们如何发现自己的代码是否有问题呢?
最好的方式就是打日志,本题的话,就是将 minDist 数组打印出来,就可以很明显发现 哪里出问题了。
每次选择节点后,minDist数组的变化是否符合预期 ,是否和我上面讲的逻辑是对应的。
例如本题,如果想debug的话,打印日志可以这样写:
class Solution {
public:
int networkDelayTime(vector<vector<int>>& times, int n, int k) {
// 注意题目中给的二维数组并不是领接矩阵
// 需要邻接矩阵来存图
// 因为本题处理方式是节点标号从1开始,所以数组的大小都是 n+1
vector<vector<int>> grid(n + 1, vector<int>(n + 1, INT_MAX));
for(int i = 0; i < times.size(); i++){
int p1 = times[i][0];
int p2 = times[i][1];
grid[p1][p2] = times[i][2];
}
// 存储从源点到每个节点的最短距离
std::vector<int> minDist(n + 1, INT_MAX);
// 记录顶点是否被访问过
std::vector<bool> visited(n + 1, false);
minDist[k] = 0; // 起始点到自身的距离为0
for (int i = 1; i <= n; i++) {
int minVal = INT_MAX;
int cur = 1;
// 遍历每个节点,选择未被访问的节点集合中哪个节点到源点的距离最小
for (int v = 1; v <= n; ++v) {
if (!visited[v] && minDist[v] <= minVal) {
minVal = minDist[v];
cur = v;
}
}
visited[cur] = true; // 标记该顶点已被访问
for (int v = 1; v <= n; v++) {
if (!visited[v] && grid[cur][v] != INT_MAX && minDist[cur] + grid[cur][v] < minDist[v]) {
minDist[v] = minDist[cur] + grid[cur][v];
}
}
// 打印日志:
cout << "select:" << cur << endl;
for (int v = 1; v <= n; v++) cout << v << ":" << minDist[v] << " ";
cout << endl << endl;;
}
// 源点到最远的节点的时间,也就是寻找 源点到所有节点最短路径的最大值
int result = 0;
for (int i = 1; i <= n; i++) {
if (minDist[i] == INT_MAX) return -1;// 没有路径
result = max(minDist[i], result);
}
return result;
}
};
打印后的结果:
select:2
1:1 2:0 3:1 4:2147483647
select:3
1:1 2:0 3:1 4:2
select:1
1:1 2:0 3:1 4:2
select:4
1:1 2:0 3:1 4:2
打印日志可以和上面我讲解的过程进行对比,每一步的结果是完全对应的。
所以如果大家如果代码有问题,打日志来debug是最好的方法
出现负数
如果图中边的权值为负数,dijkstra 还合适吗?
看一下这个图: (有负权值)
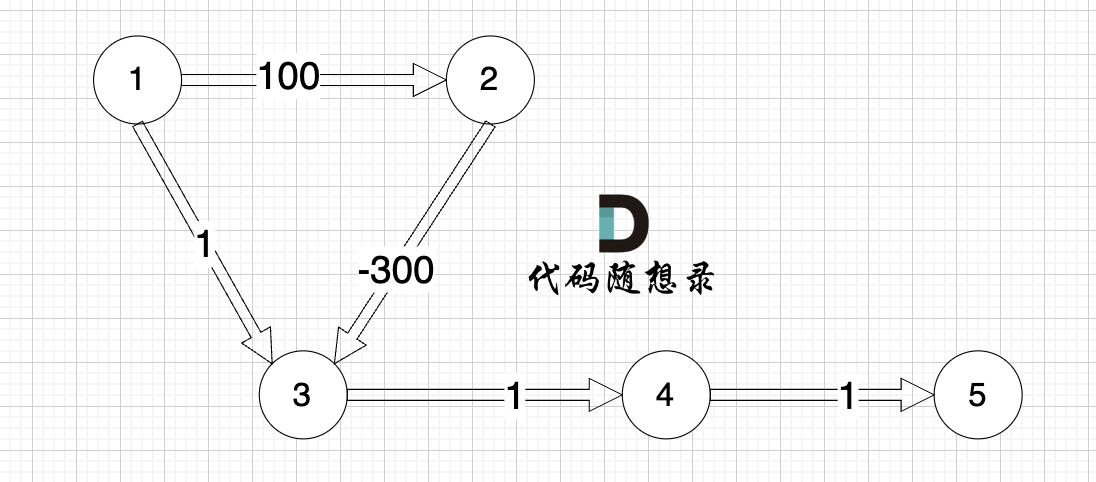
节点1 到 节点5 的最短路径 应该是 节点1 -> 节点2 -> 节点3 -> 节点4 -> 节点5
那我们来看dijkstra 求解的路径是什么样的,继续dijkstra 三部曲来模拟 :(dijkstra模拟过程上面已经详细讲过,以下只模拟重要过程,例如如何初始化就省略讲解了)
初始化:
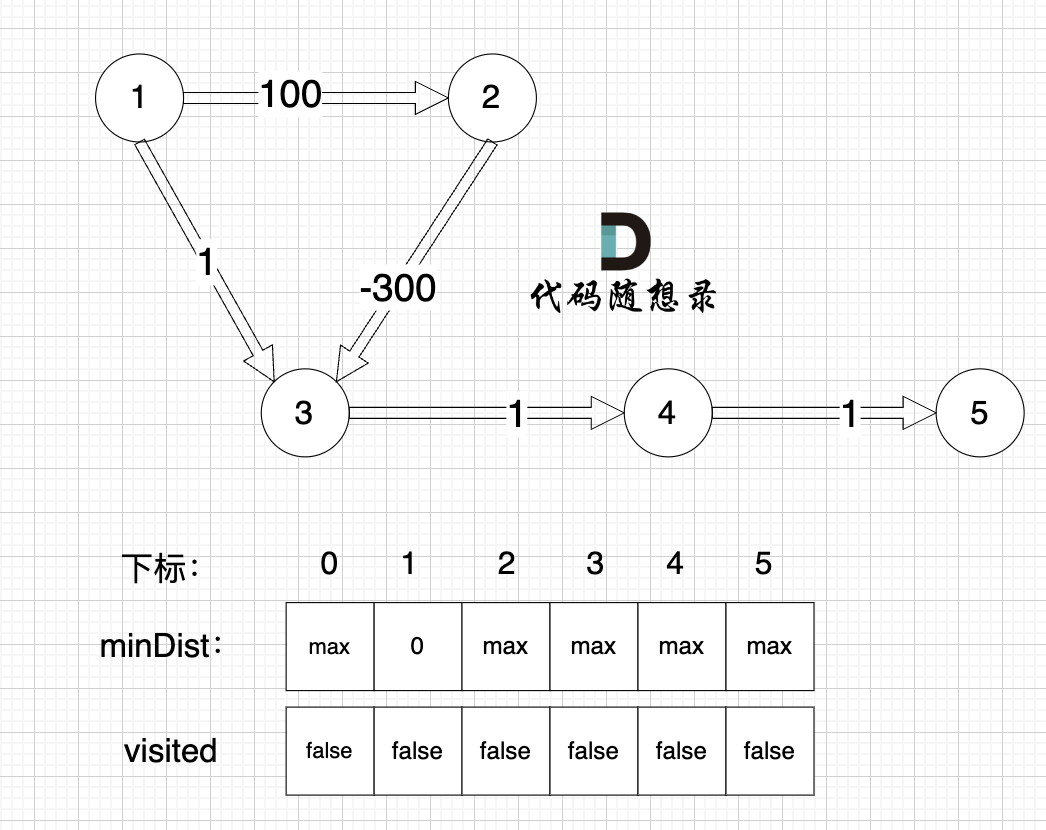
1、选源点到哪个节点近且该节点未被访问过
源点距离源点最近,距离为0,且未被访问。
2、该最近节点被标记访问过
标记源点访问过
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
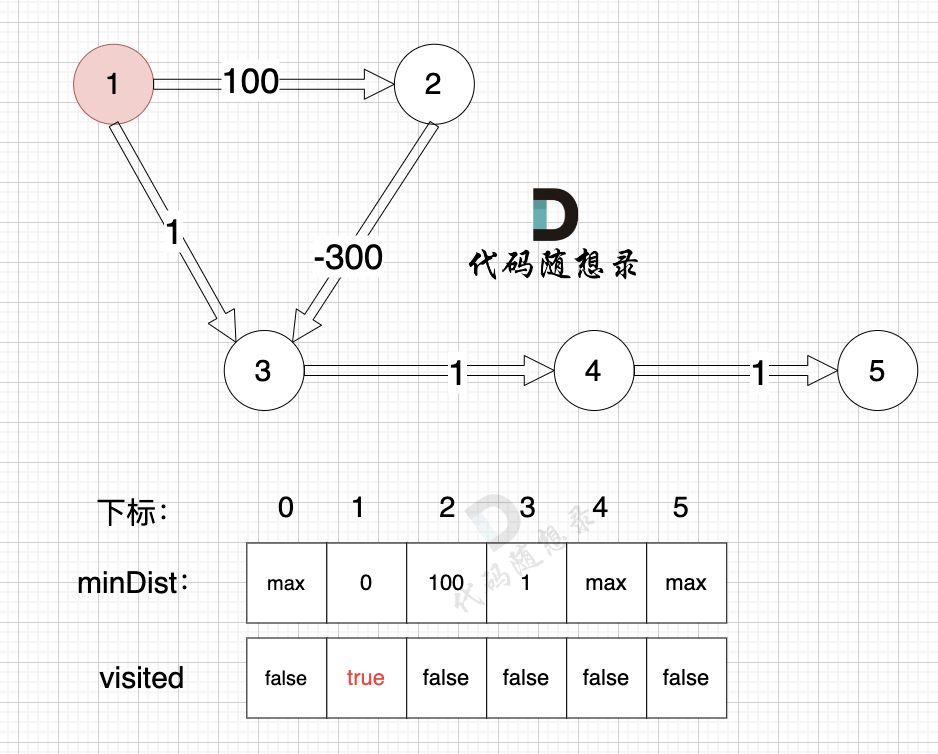
更新 minDist数组,即:源点(节点1) 到 节点2 和 节点3的距离。
- 源点到节点2的最短距离为100,小于原minDist[2]的数值max,更新minDist[2] = 100
- 源点到节点3的最短距离为1,小于原minDist[3]的数值max,更新minDist[4] = 1
1、选源点到哪个节点近且该节点未被访问过
源点距离节点3最近,距离为1,且未被访问。
2、该最近节点被标记访问过
标记节点3访问过
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
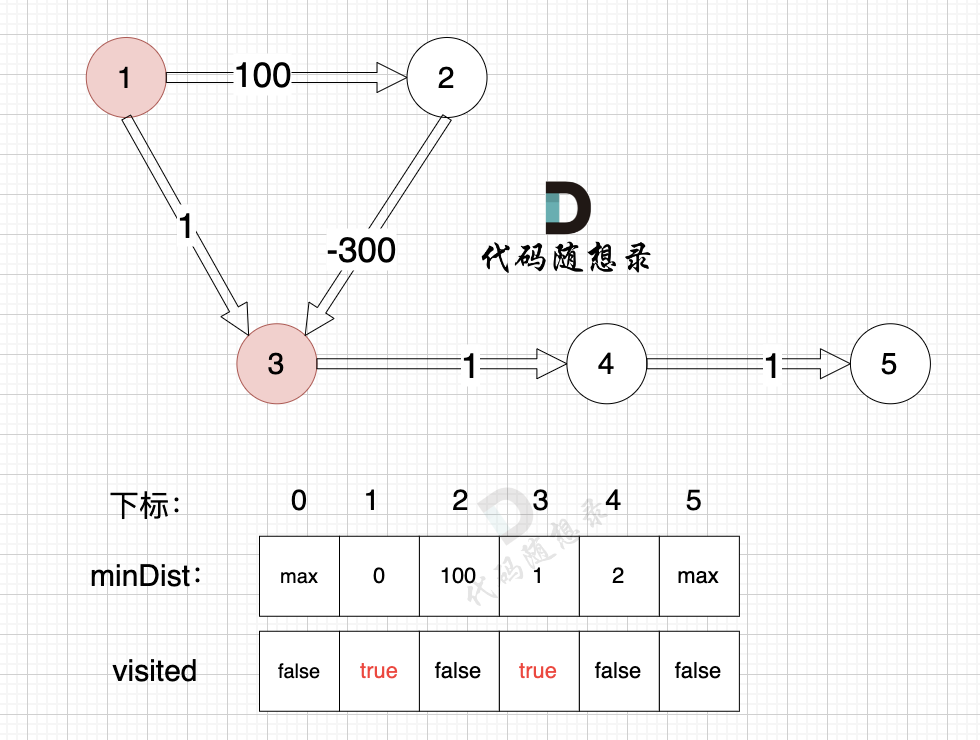
由于节点3的加入,那么源点可以有新的路径链接到节点4 所以更新minDist数组:
- 源点到节点4的最短距离为2,小于原minDist[4]的数值max,更新minDist[4] = 2
1、选源点到哪个节点近且该节点未被访问过
源点距离节点4最近,距离为2,且未被访问。
2、该最近节点被标记访问过
标记节点4访问过
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
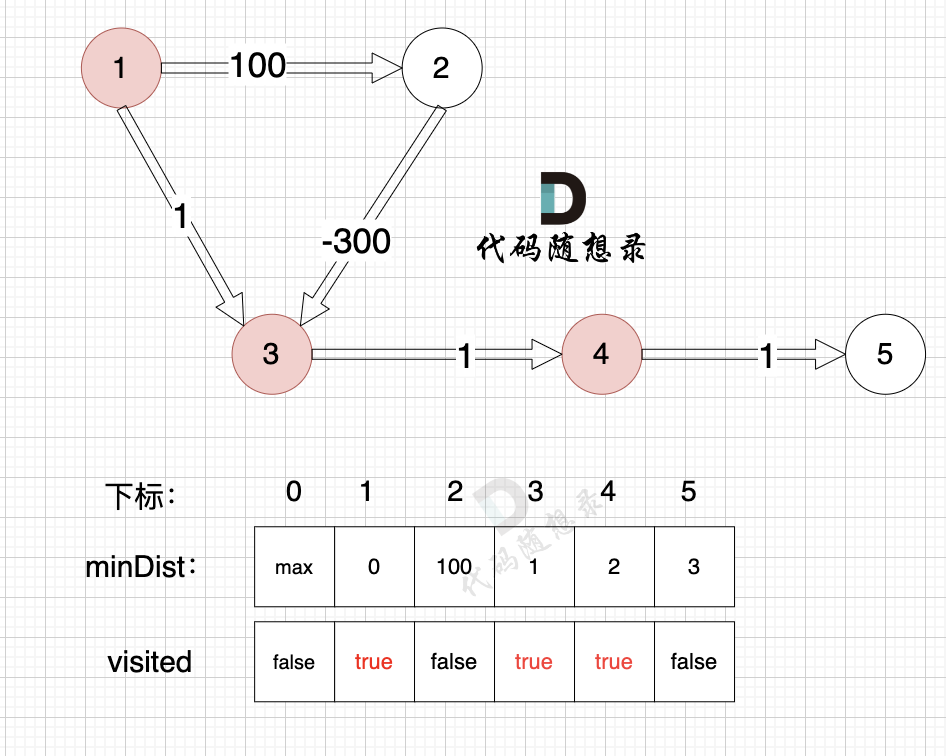
由于节点4的加入,那么源点可以有新的路径链接到节点5 所以更新minDist数组:
- 源点到节点5的最短距离为3,小于原minDist[5]的数值max,更新minDist[5] = 5
1、选源点到哪个节点近且该节点未被访问过
源点距离节点5最近,距离为3,且未被访问。
2、该最近节点被标记访问过
标记节点5访问过
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
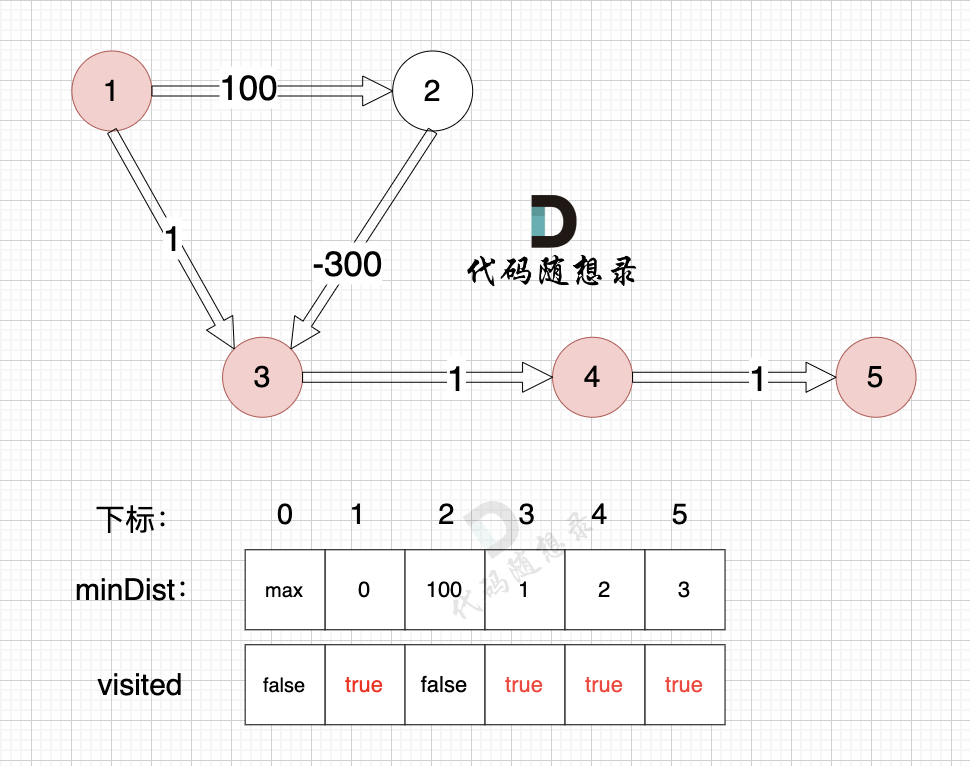
节点5的加入,而节点5 没有链接其他节点, 所以不用更新minDist数组,仅标记节点5被访问过了
1、选源点到哪个节点近且该节点未被访问过
源点距离节点2最近,距离为100,且未被访问。
2、该最近节点被标记访问过
标记节点2访问过
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
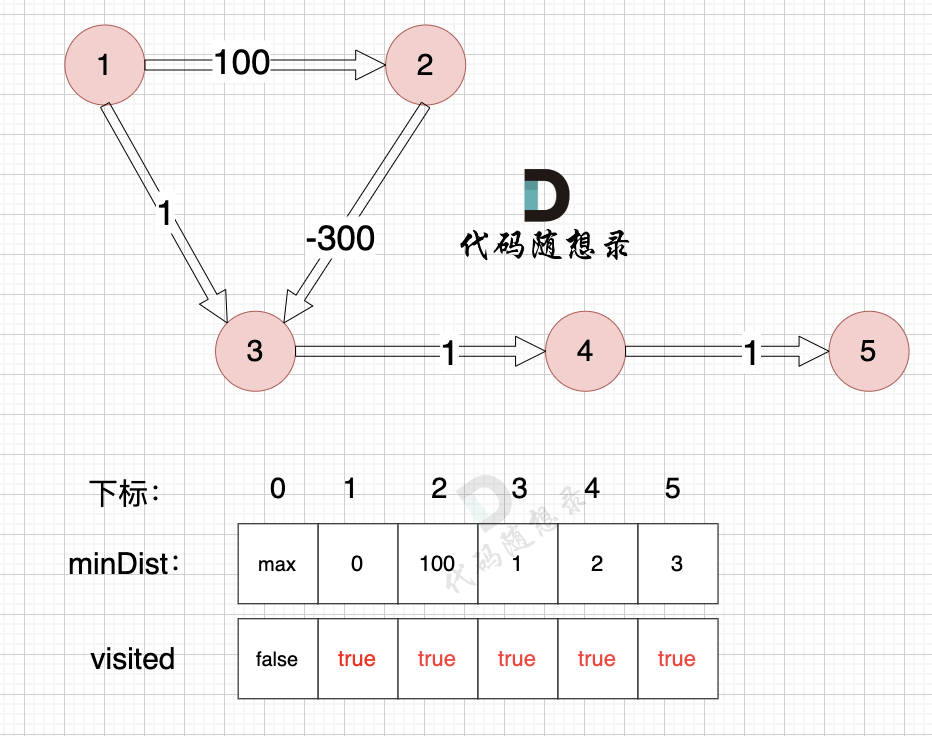
至此dijkstra的模拟过程就结束了,根据最后的minDist数组,我们求 节点1 到 节点5 的最短路径的权值总和为 3,路径: 节点1 -> 节点3 -> 节点4 -> 节点5
通过以上的过程模拟,我们可以发现 之所以 没有走有负权值的最短路径 是因为 在 访问 节点 2 的时候,节点 3 已经访问过了,就不会再更新了。
那有录友可能会想: 我可以改代码逻辑啊,访问过的节点,也让它继续访问不就好了?
那么访问过的节点还能继续访问会不会有死循环的出现呢?控制逻辑不让其死循环?那特殊情况自己能都想清楚吗?(可以试试,实践出真知)
对于负权值的出现,大家可以针对某一个场景 不断去修改 dijkstra 的代码,但最终会发现只是 拆了东墙补西墙,对dijkstra的补充逻辑只能满足某特定场景最短路求解。
对于求解带有负权值的最短路问题,可以使用 Floyd 算法 ,我在后序会详细讲解。
dijkstra与prim算法的区别
这里再次提示,需要先看我的 prim算法精讲 ,否则可能不知道我下面讲的是什么。
大家可以发现 dijkstra的代码看上去 怎么和 prim算法这么像呢。
其实代码大体不差,唯一区别在 三部曲中的 第三步: 更新minDist数组
因为prim是求 非访问节点到最小生成树的最小距离,而 dijkstra是求 非访问节点到源点的最小距离。
prim 更新 minDist数组的写法:
for (int j = 1; j <= v; j++) {
if (!isInTree[j] && grid[cur][j] < minDist[j]) {
minDist[j] = grid[cur][j];
}
}因为 minDist表示 节点到最小生成树的最小距离,所以 新节点cur的加入,只需要 使用 grid[cur][j] ,grid[cur][j] 就表示 cur 加入生成树后,生成树到 节点j 的距离。
dijkstra 更新 minDist数组的写法:
for (int v = 1; v <= n; v++) {
if (!visited[v] && grid[cur][v] != INT_MAX && minDist[cur] + grid[cur][v] < minDist[v]) {
minDist[v] = minDist[cur] + grid[cur][v];
}
}因为 minDist表示 节点到源点的最小距离,所以 新节点 cur 的加入,需要使用 源点到cur的距离 (minDist[cur]) + cur 到 节点 v 的距离 (grid[cur][v]),才是 源点到节点v的距离。
此时大家可能不禁要想 prim算法 可以有负权值吗?
当然可以!
录友们可以自己思考思考一下,这是为什么?
这里我提示一下:prim算法只需要将节点以最小权值和链接在一起,不涉及到单一路径。
总结
本篇,我们深入讲解的dijkstra算法,详细模拟其工作的流程。
这里我给出了 dijkstra 三部曲 来 帮助大家理解 该算法,不至于 每次写 dijkstra 都是黑盒操作,没有框架没有章法。
在给出的代码中,我也按照三部曲的逻辑来给大家注释,只要理解这三部曲,即使 过段时间 对 dijkstra 算法有些遗忘,依然可以写出一个框架出来,然后再去调试细节。
对于图论算法,一般代码都比较长,很难写出代码直接可以提交通过,都需要一个debug的过程,所以 学习如何debug 非常重要!
这也是我为什么 在本文中 单独用来讲解 debug方法。
本题求的是最短路径和是多少,同时我们也要掌握 如何把最短路径打印出来。
我还写了大篇幅来讲解 负权值的情况, 只有画图带大家一步一步去 看 出现负权值 dijkstra的求解过程,才能帮助大家理解,问题出在哪里。
如果我直接讲:是因为访问过的节点 不能再访问,导致错过真正的最短路,我相信大家都不知道我在说啥。
最后我还讲解了 dijkstra 和 prim 算法的 相同 与 不同之处, 我在图论的讲解安排中 先讲 prim算法 再讲 dijkstra 是有目的的, 理解这两个算法的相同与不同之处 有助于大家学习的更深入。
而不是 学了 dijkstra 就只看 dijkstra, 算法之间 都是有联系的,多去思考 算法之间的相互联系,会帮助大家思考的更深入,掌握的更彻底。
本篇写了这么长,我也只讲解了 朴素版dijkstra,关于 堆优化dijkstra,我会在下一篇再来给大家详细讲解。
堆优化版本dijkstra
本篇我们来讲解 堆优化版dijkstra,看本篇之前,一定要先看 我讲解的 朴素版dijkstra,否则本篇会有部分内容看不懂。
在上一篇中,我们讲解了朴素版的dijkstra,该解法的时间复杂度为 O(n^2),可以看出时间复杂度 只和 n (节点数量)有关系。
如果n很大的话,我们可以换一个角度来优先性能。
在 讲解 最小生成树的时候,我们 讲了两个算法,prim算法(从点的角度来求最小生成树)、Kruskal算法(从边的角度来求最小生成树)
这么在n 很大的时候,也有另一个思考维度,即:从边的数量出发。
当 n 很大,边 的数量 也很多的时候(稠密图),那么 上述解法没问题。
但 n 很大,边 的数量 很小的时候(稀疏图),是不是可以换成从边的角度来求最短路呢?
毕竟边的数量少。
有的录友可能会想,n (节点数量)很大,边不就多吗? 怎么会边的数量少呢?
别忘了,谁也没有规定 节点之间一定要有边连接着,例如有一万个节点,只有一条边,这也是一张图。
了解背景之后,再来看 解法思路。
图的存储
首先是 图的存储。
关于图的存储 主流有两种方式: 邻接矩阵和邻接表
邻接矩阵
邻接矩阵 使用 二维数组来表示图结构。 邻接矩阵是从节点的角度来表示图,有多少节点就申请多大的二维数组。
例如: grid[2][5] = 6,表示 节点 2 链接 节点5 为有向图,节点2 指向 节点5,边的权值为6 (套在题意里,可能是距离为6 或者 消耗为6 等等)
如果想表示无向图,即:grid[2][5] = 6,grid[5][2] = 6,表示节点2 与 节点5 相互连通,权值为6。
如图:
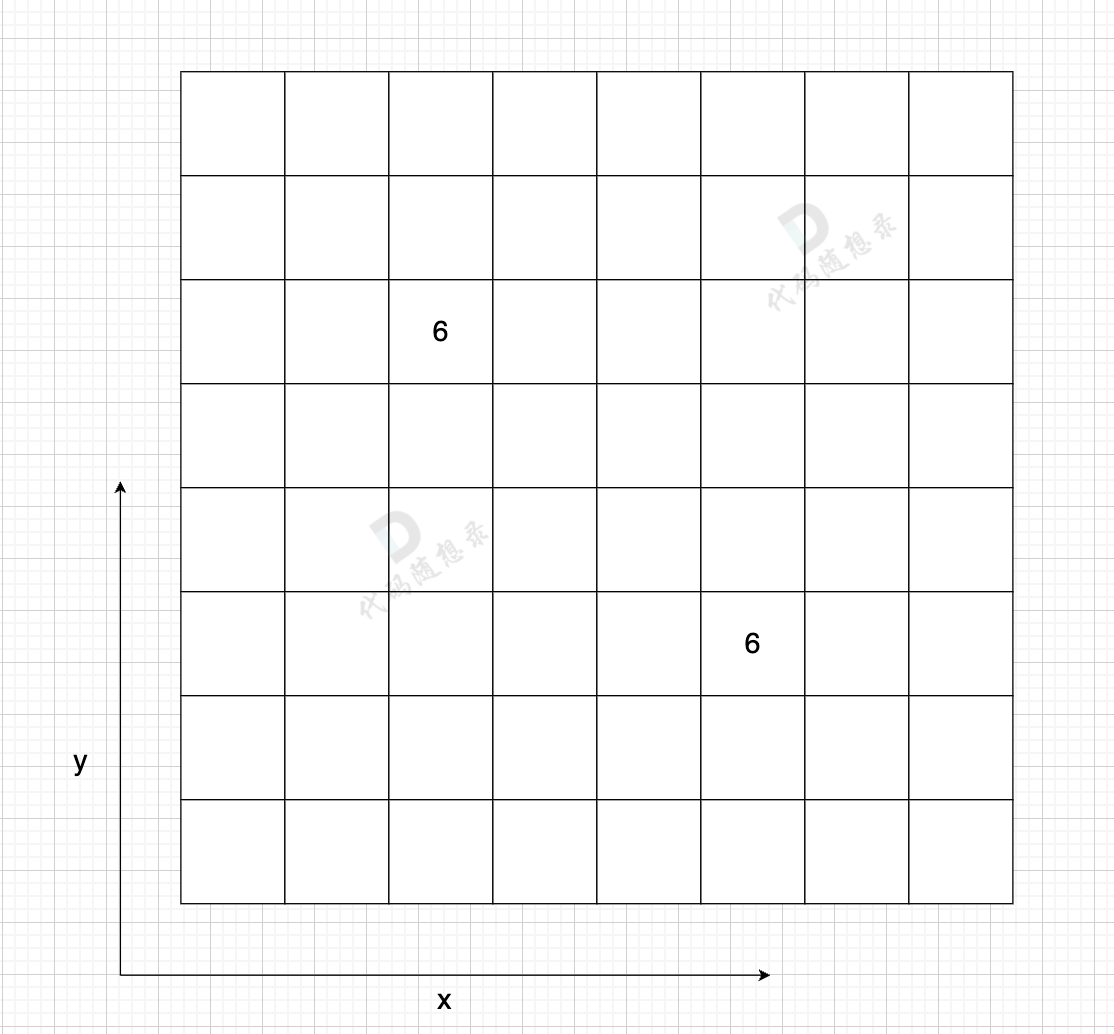
在一个 n (节点数)为8 的图中,就需要申请 8 * 8 这么大的空间,有一条双向边,即:grid[2][5] = 6,grid[5][2] = 6
这种表达方式(邻接矩阵) 在 边少,节点多的情况下,会导致申请过大的二维数组,造成空间浪费。
而且在寻找节点链接情况的时候,需要遍历整个矩阵,即 n * n 的时间复杂度,同样造成时间浪费。
邻接矩阵的优点:
- 表达方式简单,易于理解
- 检查任意两个顶点间是否存在边的操作非常快
- 适合稠密图,在边数接近顶点数平方的图中,邻接矩阵是一种空间效率较高的表示方法。
缺点:
- 遇到稀疏图,会导致申请过大的二维数组造成空间浪费 且遍历 边 的时候需要遍历整个n * n矩阵,造成时间浪费
邻接表
邻接表 使用 数组 + 链表的方式来表示。 邻接表是从边的数量来表示图,有多少边 才会申请对应大小的链表。
邻接表的构造如图:

这里表达的图是:
- 节点1 指向 节点3 和 节点5
- 节点2 指向 节点4、节点3、节点5
- 节点3 指向 节点4,节点4指向节点1。
有多少边 邻接表才会申请多少个对应的链表节点。
从图中可以直观看出 使用 数组 + 链表 来表达 边的链接情况 。
邻接表的优点:
- 对于稀疏图的存储,只需要存储边,空间利用率高
- 遍历节点链接情况相对容易
缺点:
- 检查任意两个节点间是否存在边,效率相对低,需要 O(V)时间,V表示某节点链接其他节点的数量。
- 实现相对复杂,不易理解
本题图的存储
接下来我们继续按照稀疏图的角度来分析本题。
在第一个版本的实现思路中,我们提到了三部曲:
- 第一步,选源点到哪个节点近且该节点未被访问过
- 第二步,该最近节点被标记访问过
- 第三步,更新非访问节点到源点的距离(即更新minDist数组)
在第一个版本的代码中,这三部曲是套在一个 for 循环里,为什么?
因为我们是从节点的角度来解决问题。
三部曲中第一步(选源点到哪个节点近且该节点未被访问过),这个操作本身需要for循环遍历 minDist 来寻找最近的节点。
同时我们需要 遍历所有 未访问过的节点,所以 我们从 节点角度出发,代码会有两层for循环,代码是这样的: (注意代码中的注释,标记两层for循环的用处)
for (int i = 1; i <= n; i++) { // 遍历所有节点,第一层for循环
int minVal = INT_MAX;
int cur = 1;
// 1、选距离源点最近且未访问过的节点 , 第二层for循环
for (int v = 1; v <= n; ++v) {
if (!visited[v] && minDist[v] < minVal) {
minVal = minDist[v];
cur = v;
}
}
visited[cur] = true; // 2、标记该节点已被访问
// 3、第三步,更新非访问节点到源点的距离(即更新minDist数组)
for (int v = 1; v <= n; v++) {
if (!visited[v] && grid[cur][v] != INT_MAX && minDist[cur] + grid[cur][v] < minDist[v]) {
minDist[v] = minDist[cur] + grid[cur][v];
}
}
}那么当从 边 的角度出发, 在处理 三部曲里的第一步(选源点到哪个节点近且该节点未被访问过)的时候 ,我们可以不用去遍历所有节点了。
而且 直接把 边(带权值)加入到 小顶堆(利用堆来自动排序),那么每次我们从 堆顶里 取出 边 自然就是 距离源点最近的节点所在的边。
这样我们就不需要两层for循环来寻找最近的节点了。
了解了大体思路,我们再来看代码实现。
首先是 如何使用 邻接表来表述图结构,这是摆在很多录友面前的第一个难题。
邻接表用 数组+链表 来表示,代码如下:(C++中 vector 为数组,list 为链表, 定义了 n+1 这么大的数组空间)
vector<list<int>> grid(n + 1);不少录友,不知道 如何定义的数据结构,怎么表示邻接表的,我来给大家画一个图:

图中邻接表表示:
- 节点1 指向 节点3 和 节点5
- 节点2 指向 节点4、节点3、节点5
- 节点3 指向 节点4
- 节点4 指向 节点1
大家发现图中的边没有权值,而本题中 我们的边是有权值的,权值怎么表示?在哪里表示?
所以 在vector<list<int>> grid(n + 1); 中 就不能使用int了,而是需要一个键值对 来存两个数字,一个数表示节点,一个数表示 指向该节点的这条边的权值。
那么 代码可以改成这样: (pair 为键值对,可以存放两个int)
vector<list<pair<int,int>>> grid(n + 1);举例来给大家展示 该代码表达的数据 如下:
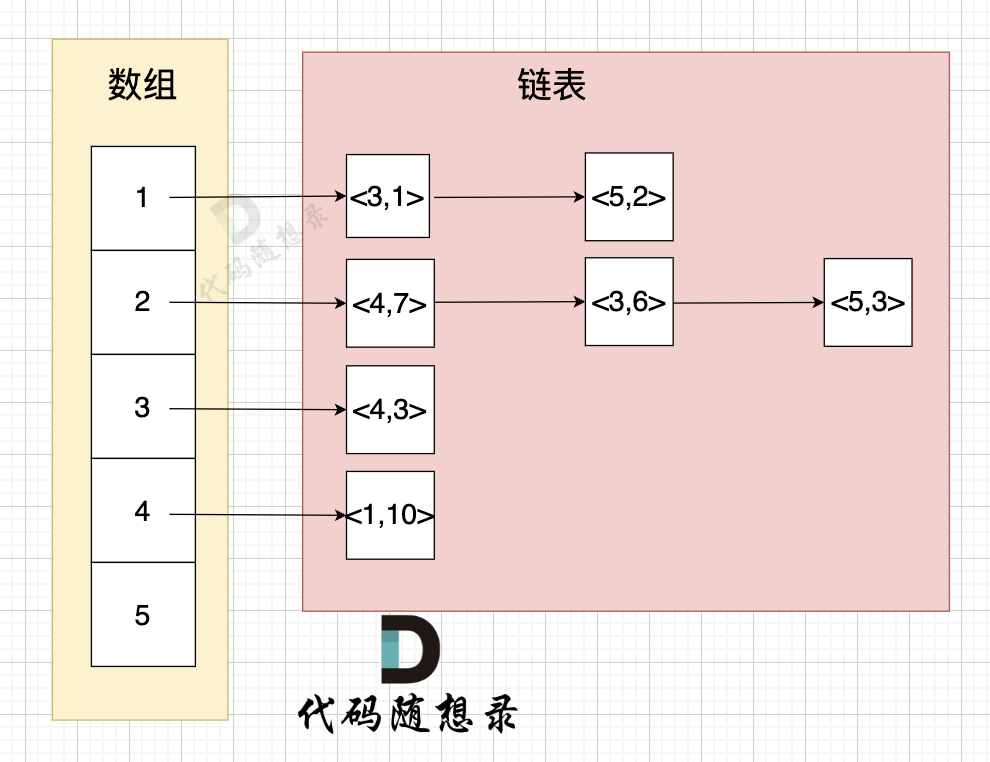
- 节点1 指向 节点3 权值为 1
- 节点1 指向 节点5 权值为 2
- 节点2 指向 节点4 权值为 7
- 节点2 指向 节点3 权值为 6
- 节点2 指向 节点5 权值为 3
- 节点3 指向 节点4 权值为 3
- 节点5 指向 节点1 权值为 10
这样 我们就把图中权值表示出来了。
但是在代码中 使用 pair<int, int> 很容易让我们搞混了,第一个int 表示什么,第二个int表示什么,导致代码可读性很差,或者说别人看你的代码看不懂。
那么 可以 定一个类 来取代 pair<int, int>
类(或者说是结构体)定义如下:
struct Edge {
int to; // 邻接顶点
int val; // 边的权重
Edge(int t, int w): to(t), val(w) {} // 构造函数
};这个类里有两个成员变量,有对应的命名,这样不容易搞混 两个int的含义。
所以 本题中邻接表的定义如下:
struct Edge {
int to; // 链接的节点
int val; // 边的权重
Edge(int t, int w): to(t), val(w) {} // 构造函数
};
vector<list<Edge>> grid(n + 1); // 邻接表
(我们在下面的讲解中会直接使用这个邻接表的代码表示方式)
堆优化细节
其实思路依然是 dijkstra 三部曲:
- 第一步,选源点到哪个节点近且该节点未被访问过
- 第二步,该最近节点被标记访问过
- 第三步,更新非访问节点到源点的距离(即更新minDist数组)
只不过之前是 通过遍历节点来遍历边,通过两层for循环来寻找距离源点最近节点。 这次我们直接遍历边,且通过堆来对边进行排序,达到直接选择距离源点最近节点。
先来看一下针对这三部曲,如果用 堆来优化。
那么三部曲中的第一步(选源点到哪个节点近且该节点未被访问过),我们如何选?
我们要选择距离源点近的节点(即:该边的权值最小),所以 我们需要一个 小顶堆 来帮我们对边的权值排序,每次从小顶堆堆顶 取边就是权值最小的边。
C++定义小顶堆,可以用优先级队列实现,代码如下:
// 小顶堆
class mycomparison {
public:
bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {
return lhs.second > rhs.second;
}
};
// 优先队列中存放 pair<节点编号,源点到该节点的权值>
priority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> pq;(pair<int, int>中 第二个int 为什么要存 源点到该节点的权值,因为 这个小顶堆需要按照权值来排序)
有了小顶堆自动对边的权值排序,那我们只需要直接从 堆里取堆顶元素(小顶堆中,最小的权值在上面),就可以取到离源点最近的节点了 (未访问过的节点,不会加到堆里进行排序)
所以三部曲中的第一步,我们不用 for循环去遍历,直接取堆顶元素:
// pair<节点编号,源点到该节点的权值>
pair<int, int> cur = pq.top(); pq.pop();
第二步(该最近节点被标记访问过) 这个就是将 节点做访问标记,和 朴素dijkstra 一样 ,代码如下:
// 2. 第二步,该最近节点被标记访问过
visited[cur.first] = true;
(cur.first 是指取 pair<int, int> 里的第一个int,即节点编号 )
第三步(更新非访问节点到源点的距离),这里的思路 也是 和朴素dijkstra一样的。
但很多录友对这里是最懵的,主要是因为两点:
- 没有理解透彻 dijkstra 的思路
- 没有理解 邻接表的表达方式
我们来回顾一下 朴素dijkstra 在这一步的代码和思路(如果没看过我讲解的朴素版dijkstra,这里会看不懂)
// 3、第三步,更新非访问节点到源点的距离(即更新minDist数组)
for (int v = 1; v <= n; v++) {
if (!visited[v] && grid[cur][v] != INT_MAX && minDist[cur] + grid[cur][v] < minDist[v]) {
minDist[v] = minDist[cur] + grid[cur][v];
}
}其中 for循环是用来做什么的? 是为了 找到 节点cur 链接指向了哪些节点,因为使用邻接矩阵的表达方式 所以把所有节点遍历一遍。
而在邻接表中,我们可以以相对高效的方式知道一个节点链接指向哪些节点。
再回顾一下邻接表的构造(数组 + 链表):

假如 加入的cur 是节点 2, 那么 grid[2] 表示的就是图中第二行链表。 (grid数组的构造我们在 上面 「图的存储」中讲过)
所以在邻接表中,我们要获取 节点cur 链接指向哪些节点,就是遍历 grid[cur节点编号] 这个链表。
这个遍历方式,C++代码如下:
for (Edge edge : grid[cur.first]) (如果不知道 Edge 是什么,看上面「图的存储」中邻接表的讲解)
cur.first 就是cur节点编号, 参考上面pair的定义: pair<节点编号,源点到该节点的权值>
接下来就是更新 非访问节点到源点的距离,代码实现和 朴素dijkstra 是一样的,代码如下:
// 3. 第三步,更新非访问节点到源点的距离(即更新minDist数组)
for (Edge edge : grid[cur.first]) { // 遍历 cur指向的节点,cur指向的节点为 edge
// cur指向的节点edge.to,这条边的权值为 edge.val
if (!visited[edge.to] && minDist[cur.first] + edge.val < minDist[edge.to]) { // 更新minDist
minDist[edge.to] = minDist[cur.first] + edge.val;
pq.push(pair<int, int>(edge.to, minDist[edge.to]));
}
}但为什么思路一样,有的录友能写出朴素dijkstra,但堆优化这里的逻辑就是写不出来呢?
主要就是因为对邻接表的表达方式不熟悉!
以上代码中,cur 链接指向的节点编号 为 edge.to, 这条边的权值为 edge.val ,如果对这里模糊的就再回顾一下 Edge的定义:
struct Edge {
int to; // 邻接顶点
int val; // 边的权重
Edge(int t, int w): to(t), val(w) {} // 构造函数
};确定该节点没有被访问过,!visited[edge.to] , 目前 源点到cur.first的最短距离(minDist) + cur.first 到 edge.to 的距离 (edge.val) 是否 小于 minDist已经记录的 源点到 edge.to 的距离 (minDist[edge.to])
如果是的话,就开始更新操作。
即:
if (!visited[edge.to] && minDist[cur.first] + edge.val < minDist[edge.to]) { // 更新minDist
minDist[edge.to] = minDist[cur.first] + edge.val;
pq.push(pair<int, int>(edge.to, minDist[edge.to])); // 由于cur节点的加入,而新链接的边,加入到优先级队里中
}
同时,由于cur节点的加入,源点又有可以新链接到的边,将这些边加入到优先级队里中。
以上代码思路 和 朴素版dijkstra 是一样一样的,主要区别是两点:
- 邻接表的表示方式不同
- 使用优先级队列(小顶堆)来对新链接的边排序
代码实现
堆优化dijkstra完整代码如下:
class Solution {
public:
// 小顶堆
class mycomparison {
public:
bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {
return lhs.second > rhs.second;
}
};
// 定义一个结构体来表示带权重的边
struct Edge {
int to; // 邻接顶点
int val; // 边的权重
Edge(int t, int w): to(t), val(w) {} // 构造函数
};
int networkDelayTime(vector<vector<int>>& times, int n, int k) {
std::vector<std::list<Edge>> grid(n + 1);
for(int i = 0; i < times.size(); i++){
int p1 = times[i][0];
int p2 = times[i][1];
// p1 指向 p2,权值为 times[i][2]
grid[p1].push_back(Edge(p2, times[i][2]));
}
// 存储从源点到每个节点的最短距离
std::vector<int> minDist(n + 1, INT_MAX);
// 记录顶点是否被访问过
std::vector<bool> visited(n + 1, false);
// 优先队列中存放 pair<节点,源点到该节点的距离>
priority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> pq;
pq.push(pair<int, int>(k, 0));
minDist[k] = 0; // 这个不要忘了
while (!pq.empty()) {
// <节点, 源点到该节点的距离>
// 1. 第一步,选源点到哪个节点近且该节点未被访问过 (通过优先级队列来实现)
pair<int, int> cur = pq.top(); pq.pop();
if (visited[cur.first]) continue;
// 2. 第二步,该最近节点被标记访问过
visited[cur.first] = true;
// 3. 第三步,更新非访问节点到源点的距离(即更新minDist数组)
for (Edge edge : grid[cur.first]) { // 遍历 cur指向的节点,cur指向的节点为 edge
// cur指向的节点edge.to,这条边的权值为 edge.val
if (!visited[edge.to] && minDist[cur.first] + edge.val < minDist[edge.to]) { // 更新minDist
minDist[edge.to] = minDist[cur.first] + edge.val;
pq.push(pair<int, int>(edge.to, minDist[edge.to]));
}
}
}
// 源点到最远的节点的时间,也就是寻找 源点到所有节点最短路径的最大值
int result = 0;
for (int i = 1; i <= n; i++) {
if (minDist[i] == INT_MAX) return -1;// 没有路径
result = max(minDist[i], result);
}
return result;
}
};
- 时间复杂度:O(ElogE) E 为边的数量
- 空间复杂度:O(N + E) N 为节点的数量
堆优化的时间复杂度 只和边的数量有关 和节点数无关,在 优先级队列中 放的也是边。
以上代码中,while (!pq.empty()) 里套了 for (Edge edge : grid[cur.first])
for 里 遍历的是 当前节点 cur 所连接边。
那 当前节点cur 所连接的边 也是不固定的, 这就让大家分不清,这时间复杂度究竟是多少?
其实 for (Edge edge : grid[cur.first]) 里最终的数据走向 是 给队列里添加边。
那么跳出局部代码,整个队列 一定是 所有边添加了一次,同时也弹出了一次。
所以边添加一次时间复杂度是 O(E), while (!pq.empty()) 里每次都要弹出一个边来进行操作,在优先级队列(小顶堆)中 弹出一个元素的时间复杂度是 O(logE) ,这是堆排序的时间复杂度。
(当然小顶堆里 是 添加元素的时候 排序,还是 取数元素的时候排序,这个无所谓,时间复杂度都是O(E),总是是一定要排序的,而小顶堆里也不会滞留元素,有多少元素添加 一定就有多少元素弹出)
所以 该算法整体时间复杂度为 O(ElogE)
网上的不少分析 会把 n (节点的数量)算进来,这个分析是有问题的,举一个极端例子,在n 为 10000,且是有一条边的 图里,以上代码,大家感觉执行了多少次?
while (!pq.empty()) 中的 pq 存的是边,其实只执行了一次。
所以该算法时间复杂度 和 节点没有关系。
至于空间复杂度,邻接表是 数组 + 链表 数组的空间 是 N ,有E条边 就申请对应多少个链表节点,所以是 复杂度是 N + E
拓展
当然也有录友可能想 堆优化dijkstra 中 我为什么一定要用邻接表呢,我就用邻接矩阵 行不行 ?
也行的。
但 正是因为稀疏图,所以我们使用堆优化的思路, 如果我们还用 邻接矩阵 去表达这个图的话,就是 一个高效的算法 使用了低效的数据结构,那么 整体算法效率 依然是低的。
如果还不清楚为什么要使用 邻接表,可以再看看上面 我在 「图的存储」标题下的讲解。
这里我也给出 邻接矩阵版本的堆优化dijkstra代码:
class Solution {
public:
// 小顶堆(按照<k ,v>中的v 来从小到大排序)
class mycomparison {
public:
bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {
return lhs.second > rhs.second;
}
};
int networkDelayTime(vector<vector<int>>& times, int n, int k) {
// 注意题目中给的二维数组并不是邻接矩阵
// 需要邻接矩阵来存图
// 因为本题处理方式是节点标号从1开始,所以数组的大小都是 n+1
vector<vector<int>> grid(n + 1, vector<int>(n + 1, INT_MAX));
for(int i = 0; i < times.size(); i++){
int p1 = times[i][0];
int p2 = times[i][1];
grid[p1][p2] = times[i][2];
}
// 存储从源点到每个节点的最短距离
std::vector<int> minDist(n + 1, INT_MAX);
// 记录顶点是否被访问过
std::vector<bool> visited(n + 1, false);
// 优先队列中存放 [节点,源点到该节点的距离]
priority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> pq;
pq.push(pair<int, int>(k, 0));
minDist[k] = 0; // 这个不要忘了
while (!pq.empty()) {
// <节点, 源点到该节点的距离>
// 1、选距离源点最近且未访问过的节点
pair<int, int> cur = pq.top(); pq.pop();
if (visited[cur.first]) continue;
// 2、标记该节点已被访问
visited[cur.first] = true;
// 3、第三步,更新非访问节点到源点的距离(即更新minDist数组)
// 遍历 cur 可以链接的节点,更新 minDist[j]
for (int j = 1; j <= n; j++) {
if (!visited[j] && grid[cur.first][j] != INT_MAX && (minDist[cur.first] + grid[cur.first][j] < minDist[j])) {
minDist[j] = minDist[cur.first] + grid[cur.first][j];
pq.push(pair<int, int>(j, minDist[j]));
}
}
}
// 源点到最远的节点的时间,也就是寻找 源点到所有节点最短路径的最大值
int result = 0;
for (int i = 1; i <= n; i++) {
if (minDist[i] == INT_MAX) return -1;// 没有路径
result = max(minDist[i], result);
}
return result;
}
};
- 时间复杂度:O(E * (N + logE)) E为边的数量,N为节点数量
- 空间复杂度:O(log(N^2))
while (!pq.empty()) 时间复杂度为 E ,while 里面 每次取元素 时间复杂度 为 logE,和 一个for循环 时间复杂度 为 N 。
所以整体是 E * (N + logE)
总结
在学习一种优化思路的时候,首先就要知道为什么要优化,遇到了什么问题。
正如我在开篇就给大家交代清楚 堆优化方式的背景。
堆优化的整体思路和 朴素版是大体一样的,区别是 堆优化从边的角度触发,且利用堆来排序。
很多录友别说写堆优化 就是看 堆优化的代码也看的很懵。
主要是因为两点:
- 不熟悉邻接表的表达方式
- 对dijkstra的实现思路还是不熟
这是我为什么 本篇花了大力气来讲解 图的存储,就是为了让大家彻底理解邻接表以及邻接表的代码写法。
至于 dijkstra的实现思路 ,朴素版 和 堆优化版本 都是 按照 dijkstra 三部曲来的。
理解了三部曲,dijkstra 的思路就是清晰的。
针对邻接表版本代码 我做了详细的 时间复杂度分析,也让录友们清楚,相对于 朴素版,时间都优化到哪了。
最后 我也给出了 邻接矩阵的版本代码,分析了这一版本的必要性以及时间复杂度。
至此通过 两篇dijkstra的文章,终于把 dijkstra 讲完了,如果大家对我讲解里所涉及的内容都吃透的话,详细对 dijkstra 算法也就理解到位了。
这里在给出本题的Bellman_ford解法,关于 Bellman_ford ,后面我会专门来讲解的,Bellman_ford 有其独特的应用场景
class Solution {
public:
int networkDelayTime(vector<vector<int>>& times, int n, int k) {
vector<int> minDist(n + 1 , INT_MAX/2);
minDist[k] = 0;
//vector<int> minDist_copy(n); // 用来记录每一次遍历的结果
for (int i = 1; i <= n + 1; i++) {
//minDist_copy = minDist; // 获取上一次计算的结果
for (auto &f : times) {
int from = f[0];
int to = f[1];
int price = f[2];
if (minDist[to] > minDist[from] + price) minDist[to] = minDist[from] + price;
}
}
int result = 0;
for (int i = 1;i <= n; i++) {
if (minDist[i] == INT_MAX/2) return -1;// 没有路径
result = max(minDist[i], result);
}
return result;
}
};