最短路算法总结篇
至此已经讲解了四大最短路算法,分别是Dijkstra、Bellman_ford、SPFA 和 Floyd。
针对这四大最短路算法,我用了七篇长文才彻底讲清楚,分别是:
- dijkstra朴素版
- dijkstra堆优化版
- Bellman_ford
- Bellman_ford 队列优化算法(又名SPFA)
- bellman_ford 算法判断负权回路
- bellman_ford之单源有限最短路
- Floyd 算法精讲
- 启发式搜索:A * 算法
最短路算法比较复杂,而且各自有各自的应用场景,我来用一张表把讲过的最短路算法的使用场景都展现出来:
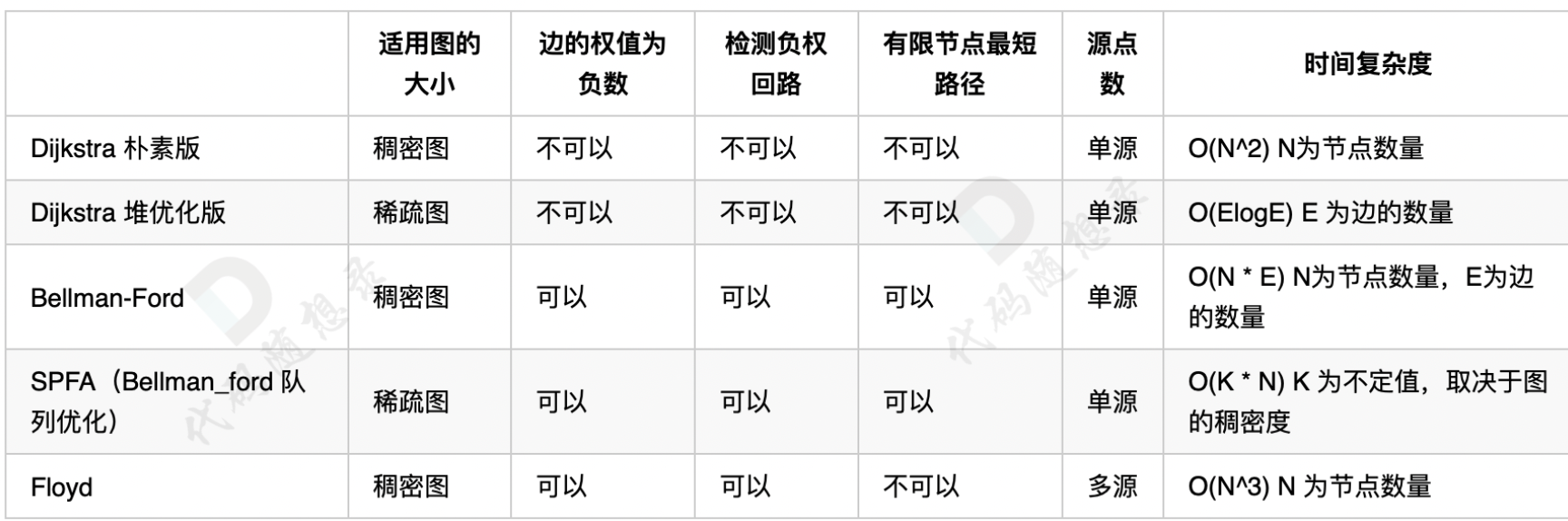
(因为A * 属于启发式搜索,和上面最短路算法并不是一类,不适合一起对比,所以没有放在一起)
可能有同学感觉:这个表太复杂了,我记也记不住。
其实记不住的原因还是对 这几个最短路算法没有深刻的理解。
这里我给大家一个大体使用场景的分析:
如果遇到单源且边为正数,直接Dijkstra。
至于 使用朴素版还是 堆优化版 还是取决于图的稠密度, 多少节点多少边算是稠密图,多少算是稀疏图,这个没有量化,如果想量化只能写出两个版本然后做实验去测试,不同的判题机得出的结果还不太一样。
一般情况下,可以直接用堆优化版本。
如果遇到单源边可为负数,直接 Bellman-Ford,同样 SPFA 还是 Bellman-Ford 取决于图的稠密度。
一般情况下,直接用 SPFA。
如果有负权回路,优先 Bellman-Ford, 如果是有限节点最短路 也优先 Bellman-Ford,理由是写代码比较方便。
如果是遇到多源点求最短路,直接 Floyd。
除非 源点特别少,且边都是正数,那可以 多次 Dijkstra 求出最短路径,但这种情况很少,一般出现多个源点了,就是想让你用 Floyd 了。
对于A * ,由于其高效性,所以在实际工程应用中使用最为广泛 ,由于其 结果的不唯一性,也就是可能是次短路的特性,一般不适合作为算法题。
游戏开发、地图导航、数据包路由等都广泛使用 A * 算法。