参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
685.冗余连接II
在本问题中,有根树指满足以下条件的 有向 图。该树只有一个根节点,所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点,而根节点没有父节点。
输入一个有向图,该图由一个有着 n 个节点(节点值不重复,从 1 到 n)的树及一条附加的有向边构成。附加的边包含在 1 到 n 中的两个不同顶点间,这条附加的边不属于树中已存在的边。
结果图是一个以边组成的二维数组 edges 。 每个元素是一对 [ui, vi],用以表示 有向 图中连接顶点 ui 和顶点 vi 的边,其中 ui 是 vi 的一个父节点。
返回一条能删除的边,使得剩下的图是有 n 个节点的有根树。若有多个答案,返回最后出现在给定二维数组的答案。
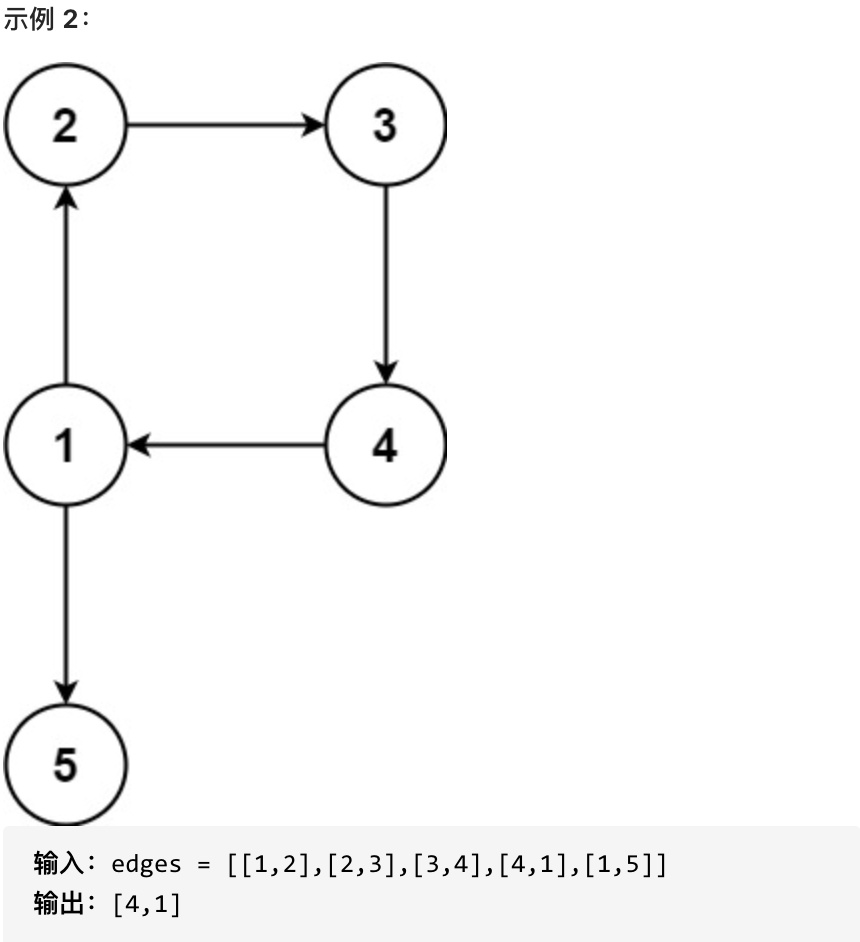
提示:
- n == edges.length
- 3 <= n <= 1000
- edges[i].length == 2
- 1 <= ui, vi <= n
思路
先重点读懂题目中的这句该图由一个有着N个节点 (节点值不重复1, 2, …, N) 的树及一条附加的边构成。附加的边的两个顶点包含在1到N中间,这条附加的边不属于树中已存在的边。
这说明题目中的图原本是是一棵树,只不过在不增加节点的情况下多加了一条边!
还有**若有多个答案,返回最后出现在给定二维数组的答案。**这说明在两条边都可以删除的情况下,要删顺序靠后的!
那么有如下三种情况,前两种情况是出现入度为2的点,如图:

且只有一个节点入度为2,为什么不看出度呢,出度没有意义,一棵树中随便一个父节点就有多个出度。
第三种情况是没有入度为2的点,那么图中一定出现了有向环(注意这里强调是有向环!)
如图:

首先先计算节点的入度,这里不少录友在计算入度的时候就搞蒙了,分不清 edges[i][j] 表示的都是什么。
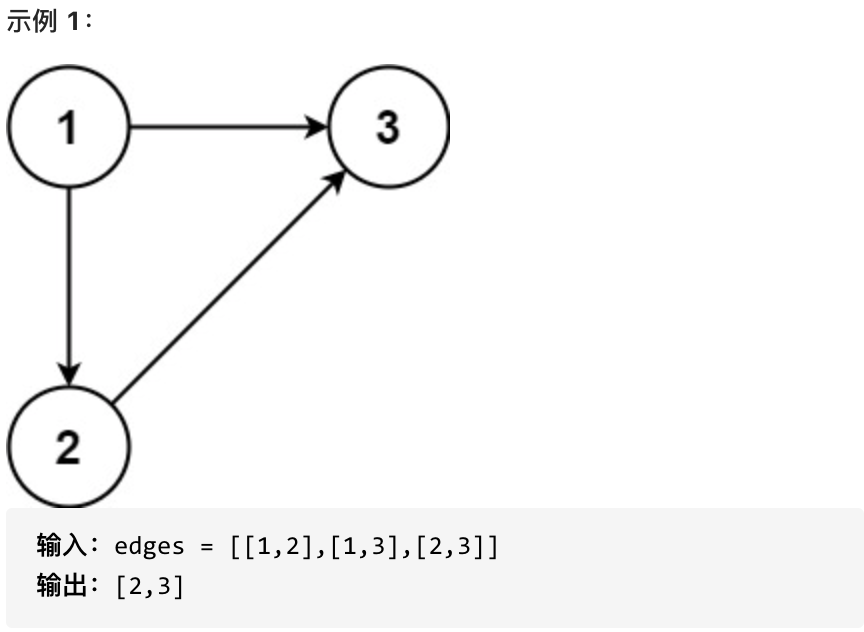
例如题目示例一给的是:edges = [[1,2],[1,3],[2,3]]
那大家很自然就想 对应二维数组的数值是: edges[1][2] ,edges[1][3],edges[2][3],但又想不出来 edges[1][2] 数值又是什么呢? 越想约懵。
其实 edges = [[1,2],[1,3],[2,3]],表示的是
edges[0][0] = 1,edges[0][1] = 2,
edges[1][0] = 1,edges[1][1] = 3,
edges[2][0] = 2,edges[2][1] = 3,
二维数组大家都学过,但是往往和图结合在一起的时候,就非常容易搞混,哪里是数组,哪里是下标了。
搞清楚之后,我们如何统计入度呢?
即 edges[i][1] 表示的节点都是 箭头指向的节点,即这个节点有一个入度! (如果想统计出度,那么就是 edges[i][0])。
所以,统计入度的代码如下:
int inDegree[N] = {0}; // 记录节点入度
n = edges.size(); // 边的数量
for (int i = 0; i < n; i++) {
inDegree[edges[i][1]]++; // 统计入度
}前两种入度为2的情况,一定是删除指向入度为2的节点的两条边其中的一条,如果删了一条,判断这个图是一个树,那么这条边就是答案,同时注意要从后向前遍历,因为如果两条边删哪一条都可以成为树,就删最后那一条。
代码如下:
vector<int> vec; // 记录入度为2的边(如果有的话就两条边)
// 找入度为2的节点所对应的边,注意要倒序,因为优先返回最后出现在二维数组中的答案
for (int i = n - 1; i >= 0; i--) {
if (inDegree[edges[i][1]] == 2) {
vec.push_back(i);
}
}
// 处理图中情况1 和 情况2
// 如果有入度为2的节点,那么一定是两条边里删一个,看删哪个可以构成树
if (vec.size() > 0) {
if (isTreeAfterRemoveEdge(edges, vec[0])) {
return edges[vec[0]];
} else {
return edges[vec[1]];
}
}在来看情况三,明确没有入度为2的情况,那么一定有向环,找到构成环的边就是要删除的边。
可以定义一个函数,代码如下:
// 在有向图里找到删除的那条边,使其变成树,返回值就是要删除的边
vector<int> getRemoveEdge(const vector<vector<int>>& edges)大家应该知道了,我们要实现两个最为关键的函数:
isTreeAfterRemoveEdge()判断删一个边之后是不是树了getRemoveEdge确定图中一定有了有向环,那么要找到需要删除的那条边
此时应该是用到并查集了,并查集为什么可以判断 一个图是不是树呢?
因为如果两个点所在的边在添加图之前如果就可以在并查集里找到了相同的根,那么这条边添加上之后 这个图一定不是树了
如果还不了解并查集,可以看这里:并查集理论基础
本题C++代码如下:(详细注释了)
class Solution {
private:
static const int N = 1010; // 如题:二维数组大小的在3到1000范围内
int father[N];
int n; // 边的数量
// 并查集初始化
void init() {
for (int i = 1; i <= n; ++i) {
father[i] = i;
}
}
// 并查集里寻根的过程
int find(int u) {
return u == father[u] ? u : father[u] = find(father[u]);
}
// 将v->u 这条边加入并查集
void join(int u, int v) {
u = find(u);
v = find(v);
if (u == v) return ;
father[v] = u;
}
// 判断 u 和 v是否找到同一个根
bool same(int u, int v) {
u = find(u);
v = find(v);
return u == v;
}
// 在有向图里找到删除的那条边,使其变成树
vector<int> getRemoveEdge(const vector<vector<int>>& edges) {
init(); // 初始化并查集
for (int i = 0; i < n; i++) { // 遍历所有的边
if (same(edges[i][0], edges[i][1])) { // 构成有向环了,就是要删除的边
return edges[i];
}
join(edges[i][0], edges[i][1]);
}
return {};
}
// 删一条边之后判断是不是树
bool isTreeAfterRemoveEdge(const vector<vector<int>>& edges, int deleteEdge) {
init(); // 初始化并查集
for (int i = 0; i < n; i++) {
if (i == deleteEdge) continue;
if (same(edges[i][0], edges[i][1])) { // 构成有向环了,一定不是树
return false;
}
join(edges[i][0], edges[i][1]);
}
return true;
}
public:
vector<int> findRedundantDirectedConnection(vector<vector<int>>& edges) {
int inDegree[N] = {0}; // 记录节点入度
n = edges.size(); // 边的数量
for (int i = 0; i < n; i++) {
inDegree[edges[i][1]]++; // 统计入度
}
vector<int> vec; // 记录入度为2的边(如果有的话就两条边)
// 找入度为2的节点所对应的边,注意要倒序,因为优先返回最后出现在二维数组中的答案
for (int i = n - 1; i >= 0; i--) {
if (inDegree[edges[i][1]] == 2) {
vec.push_back(i);
}
}
// 处理图中情况1 和 情况2
// 如果有入度为2的节点,那么一定是两条边里删一个,看删哪个可以构成树
if (vec.size() > 0) {
if (isTreeAfterRemoveEdge(edges, vec[0])) {
return edges[vec[0]];
} else {
return edges[vec[1]];
}
}
// 处理图中情况3
// 明确没有入度为2的情况,那么一定有有向环,找到构成环的边返回就可以了
return getRemoveEdge(edges);
}
};其他语言版本
Java
class Solution {
private static final int N = 1010; // 如题:二维数组大小的在3到1000范围内
private int[] father;
public Solution() {
father = new int[N];
// 并查集初始化
for (int i = 0; i < N; ++i) {
father[i] = i;
}
}
// 并查集里寻根的过程
private int find(int u) {
if(u == father[u]) {
return u;
}
father[u] = find(father[u]);
return father[u];
}
// 将v->u 这条边加入并查集
private void join(int u, int v) {
u = find(u);
v = find(v);
if (u == v) return ;
father[v] = u;
}
// 判断 u 和 v是否找到同一个根,本题用不上
private Boolean same(int u, int v) {
u = find(u);
v = find(v);
return u == v;
}
/**
* 初始化并查集
*/
private void initFather() {
// 并查集初始化
for (int i = 0; i < N; ++i) {
father[i] = i;
}
}
/**
* 在有向图里找到删除的那条边,使其变成树
* @param edges
* @return 要删除的边
*/
private int[] getRemoveEdge(int[][] edges) {
initFather();
for(int i = 0; i < edges.length; i++) {
if(same(edges[i][0], edges[i][1])) { // 构成有向环了,就是要删除的边
return edges[i];
}
join(edges[i][0], edges[i][1]);
}
return null;
}
/**
* 删一条边之后判断是不是树
* @param edges
* @param deleteEdge 要删除的边
* @return true: 是树, false: 不是树
*/
private Boolean isTreeAfterRemoveEdge(int[][] edges, int deleteEdge)
{
initFather();
for(int i = 0; i < edges.length; i++)
{
if(i == deleteEdge) continue;
if(same(edges[i][0], edges[i][1])) { // 构成有向环了,一定不是树
return false;
}
join(edges[i][0], edges[i][1]);
}
return true;
}
public int[] findRedundantDirectedConnection(int[][] edges) {
int[] inDegree = new int[N];
for(int i = 0; i < edges.length; i++)
{
// 入度
inDegree[ edges[i][1] ] += 1;
}
// 找入度为2的节点所对应的边,注意要倒序,因为优先返回最后出现在二维数组中的答案
ArrayList<Integer> twoDegree = new ArrayList<Integer>();
for(int i = edges.length - 1; i >= 0; i--)
{
if(inDegree[edges[i][1]] == 2) {
twoDegree.add(i);
}
}
// 处理图中情况1 和 情况2
// 如果有入度为2的节点,那么一定是两条边里删一个,看删哪个可以构成树
if(!twoDegree.isEmpty())
{
if(isTreeAfterRemoveEdge(edges, twoDegree.get(0))) {
return edges[ twoDegree.get(0)];
}
return edges[ twoDegree.get(1)];
}
// 明确没有入度为2的情况,那么一定有有向环,找到构成环的边返回就可以了
return getRemoveEdge(edges);
}
}Python
class Solution:
def __init__(self):
self.n = 1010
self.father = [i for i in range(self.n)]
def find(self, u: int):
"""
并查集里寻根的过程
"""
if u == self.father[u]:
return u
self.father[u] = self.find(self.father[u])
return self.father[u]
def join(self, u: int, v: int):
"""
将v->u 这条边加入并查集
"""
u = self.find(u)
v = self.find(v)
if u == v : return
self.father[v] = u
pass
def same(self, u: int, v: int ):
"""
判断 u 和 v是否找到同一个根,本题用不上
"""
u = self.find(u)
v = self.find(v)
return u == v
def init_father(self):
self.father = [i for i in range(self.n)]
pass
def getRemoveEdge(self, edges: List[List[int]]) -> List[int]:
"""
在有向图里找到删除的那条边,使其变成树
"""
self.init_father()
for i in range(len(edges)):
if self.same(edges[i][0], edges[i][1]): # 构成有向环了,就是要删除的边
return edges[i]
self.join(edges[i][0], edges[i][1]);
return []
def isTreeAfterRemoveEdge(self, edges: List[List[int]], deleteEdge: int) -> bool:
"""
删一条边之后判断是不是树
"""
self.init_father()
for i in range(len(edges)):
if i == deleteEdge: continue
if self.same(edges[i][0], edges[i][1]): # 构成有向环了,一定不是树
return False
self.join(edges[i][0], edges[i][1]);
return True
def findRedundantDirectedConnection(self, edges: List[List[int]]) -> List[int]:
inDegree = [0 for i in range(self.n)]
for i in range(len(edges)):
inDegree[ edges[i][1] ] += 1
# 找入度为2的节点所对应的边,注意要倒序,因为优先返回最后出现在二维数组中的答案
towDegree = []
for i in range(len(edges))[::-1]:
if inDegree[edges[i][1]] == 2 :
towDegree.append(i)
# 处理图中情况1 和 情况2
# 如果有入度为2的节点,那么一定是两条边里删一个,看删哪个可以构成树
if len(towDegree) > 0:
if(self.isTreeAfterRemoveEdge(edges, towDegree[0])) :
return edges[towDegree[0]]
return edges[towDegree[1]]
# 明确没有入度为2的情况,那么一定有有向环,找到构成环的边返回就可以了
return self.getRemoveEdge(edges)Go
// 全局变量
var (
n = 1010// 节点数量3 到 1000
father = make([]int, n)
)
// 并查集初始化
func initialize() {
for i := 0; i < n; i++ {
father[i] = i
}
}
// 并查集里寻根的过程
func find(u int) int {
if u == father[u] {
return u
}
father[u] = find(father[u])
return father[u]
}
// 将v->u 这条边加入并查集
func join(u, v int) {
u = find(u)
v = find(v)
if u == v {
return
}
father[v] = u
}
// 判断 u 和 v是否找到同一个根,本题用不上
func same(u, v int) bool {
u = find(u)
v = find(v)
return u == v
}
// getRemoveEdge 在有向图里找到删除的那条边,使其变成树
func getRemoveEdge(edges [][]int) []int {
initialize()
for i := 0; i < len(edges); i++ { // 遍历所有的边
if same(edges[i][0], edges[i][1]) { // 构成有向环了,就是要删除的边
return edges[i]
}
join(edges[i][0], edges[i][1])
}
return []int{}
}
// isTreeAfterRemoveEdge 删一条边之后判断是不是树
func isTreeAfterRemoveEdge(edges [][]int, deleteEdge int) bool {
initialize()
for i := 0; i < len(edges); i++ {
if i == deleteEdge {
continue
}
if same(edges[i][0], edges[i][1]) { // 构成有向环了,一定不是树
return false
}
join(edges[i][0], edges[i][1])
}
return true
}
func findRedundantDirectedConnection(edges [][]int) []int {
inDegree := make([]int, len(father))
for i := 0; i < len(edges); i++ {
// 统计入度
inDegree[edges[i][1]] += 1
}
// 记录入度为2的边(如果有的话就两条边)
// 找入度为2的节点所对应的边,注意要倒序,因为优先返回最后出现在二维数组中的答案
twoDegree := make([]int, 0)
for i := len(edges) - 1; i >= 0; i-- {
if inDegree[edges[i][1]] == 2 {
twoDegree = append(twoDegree, i)
}
}
// 处理图中情况1 和 情况2
// 如果有入度为2的节点,那么一定是两条边里删一个,看删哪个可以构成树
if len(twoDegree) > 0 {
if isTreeAfterRemoveEdge(edges, twoDegree[0]) {
return edges[twoDegree[0]]
}
return edges[twoDegree[1]]
}
// 处理图中情况3
// 明确没有入度为2的情况,那么一定有有向环,找到构成环的边返回就可以了
return getRemoveEdge(edges)
}
JavaScript
const N = 1010; // 如题:二维数组大小的在3到1000范围内
const father = new Array(N);
let n; // 边的数量
// 并查集里寻根的过程
const find = u => {
return u == father[u] ? u : father[u] = find(father[u]);
};
// 将v->u 这条边加入并查集
const join = (u, v) => {
u = find(u);
v = find(v);
if(u == v) return;
father[v] = u;
};
// 判断 u 和 v是否找到同一个根
const same = (u, v) => {
u = find(u);
v = find(v);
return u == v;
};
// 在有向图里找到删除的那条边,使其变成树
const getRemoveEdge = edges => {
// 初始化并查集
for (let i = 1; i <= n; i++) {
father[i] = i;
}
for (let i = 0; i < n; i++) { // 遍历所有的边
if (same(edges[i][0], edges[i][1])) { // 构成有向环了,就是要删除的边
return edges[i];
}
join(edges[i][0], edges[i][1]);
}
return [];
}
// 删一条边之后判断是不是树
const isTreeAfterRemoveEdge = (edges, deleteEdge) => {
// 初始化并查集
for (let i = 1; i <= n; i++) {
father[i] = i;
}
for (let i = 0; i < n; i++) {
if (i == deleteEdge) continue;
if (same(edges[i][0], edges[i][1])) { // 构成有向环了,一定不是树
return false;
}
join(edges[i][0], edges[i][1]);
}
return true;
}
/**
* @param {number[][]} edges
* @return {number[]}
*/
var findRedundantDirectedConnection = function(edges) {
n = edges.length;// 边的数量
const inDegree = new Array(n+1).fill(0); // 记录节点入度
for (let i = 0; i < n; i++) {
inDegree[edges[i][1]]++; // 统计入度
}
let vec = [];// 记录入度为2的边(如果有的话就两条边)
// 找入度为2的节点所对应的边,注意要倒序,因为优先返回最后出现在二维数组中的答案
for (let i = n - 1; i >= 0; i--) {
if (inDegree[edges[i][1]] == 2) {
vec.push(i);
}
}
// 处理图中情况1 和 情况2
// 如果有入度为2的节点,那么一定是两条边里删一个,看删哪个可以构成树
if (vec.length > 0) {
if (isTreeAfterRemoveEdge(edges, vec[0])) {
return edges[vec[0]];
} else {
return edges[vec[1]];
}
}
// 处理图中情况3
// 明确没有入度为2的情况,那么一定有有向环,找到构成环的边返回就可以了
return getRemoveEdge(edges);
};
