烧饼排序

通知:数据结构精品课 和 递归算法专题课 限时附赠网站会员,全新纸质书《labuladong 的算法笔记》 出版,签名版限时半价!另外,建议你在我的 网站 学习文章,体验更好。
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
| LeetCode | 力扣 | 难度 |
|---|---|---|
| 969. Pancake Sorting | 969. 煎饼排序 | 🟠 |
-----------
力扣第 969 题「煎饼排序」是个很有意思的实际问题:假设盘子上有 n 块面积大小不一的烧饼,你如何用一把锅铲进行若干次翻转,让这些烧饼的大小有序(小的在上,大的在下)?
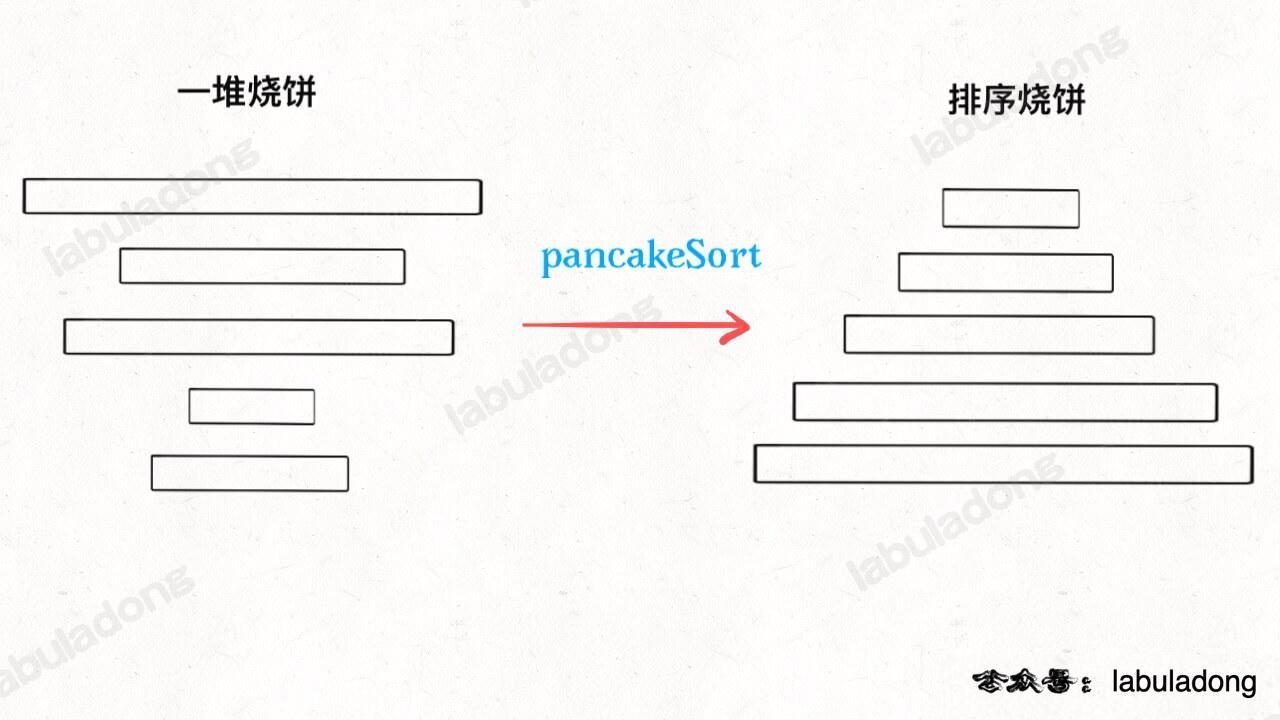
设想一下用锅铲翻转一堆烧饼的情景,其实是有一点限制的,我们每次只能将最上面的若干块饼子翻转:
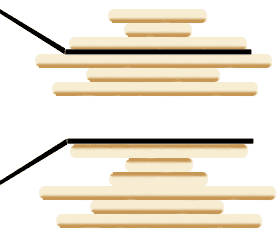
我们的问题是,如何使用算法得到一个翻转序列,使得烧饼堆变得有序?
首先,需要把这个问题抽象,用数组来表示烧饼堆:
如何解决这个问题呢?其实类似上篇文章 递归反转链表的一部分,这也是需要递归思想的。
一、思路分析
为什么说这个问题有递归性质呢?比如说我们需要实现这样一个函数:
// cakes 是一堆烧饼,函数会将前 n 个烧饼排序
void sort(int[] cakes, int n);如果我们找到了前 n 个烧饼中最大的那个,然后设法将这个饼子翻转到最底下:
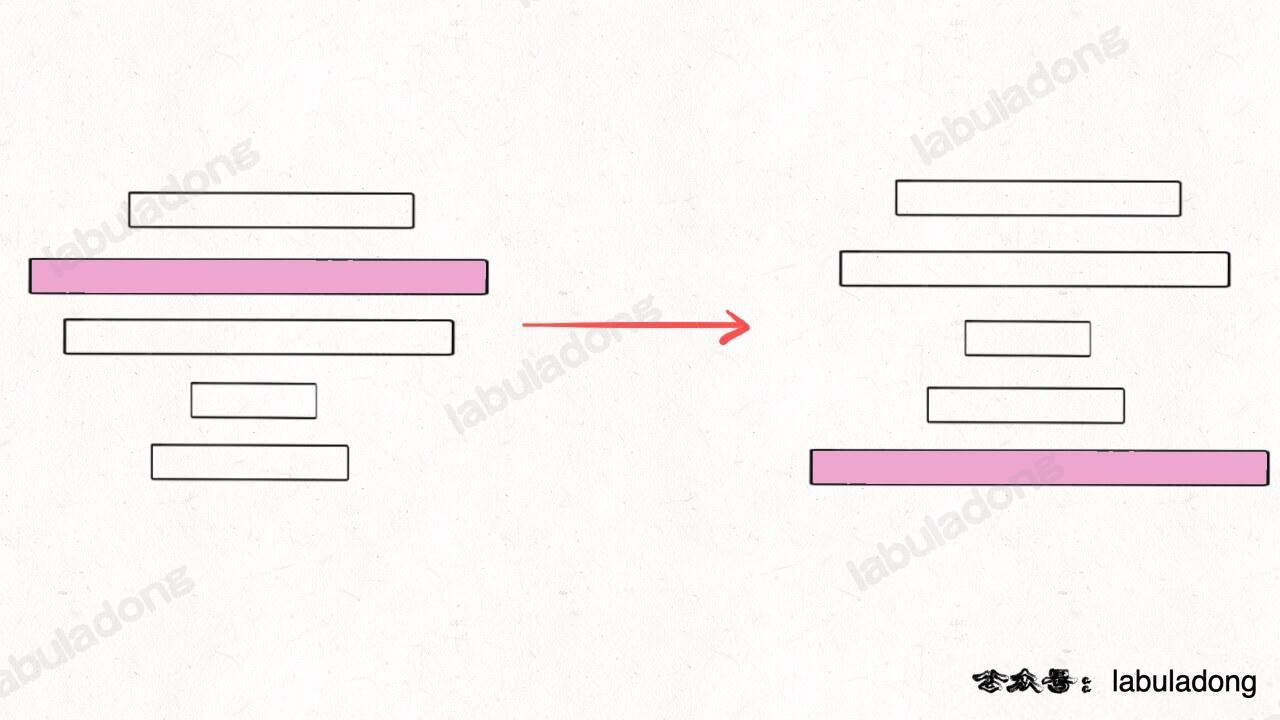
那么,原问题的规模就可以减小,递归调用 pancakeSort(A, n-1) 即可:
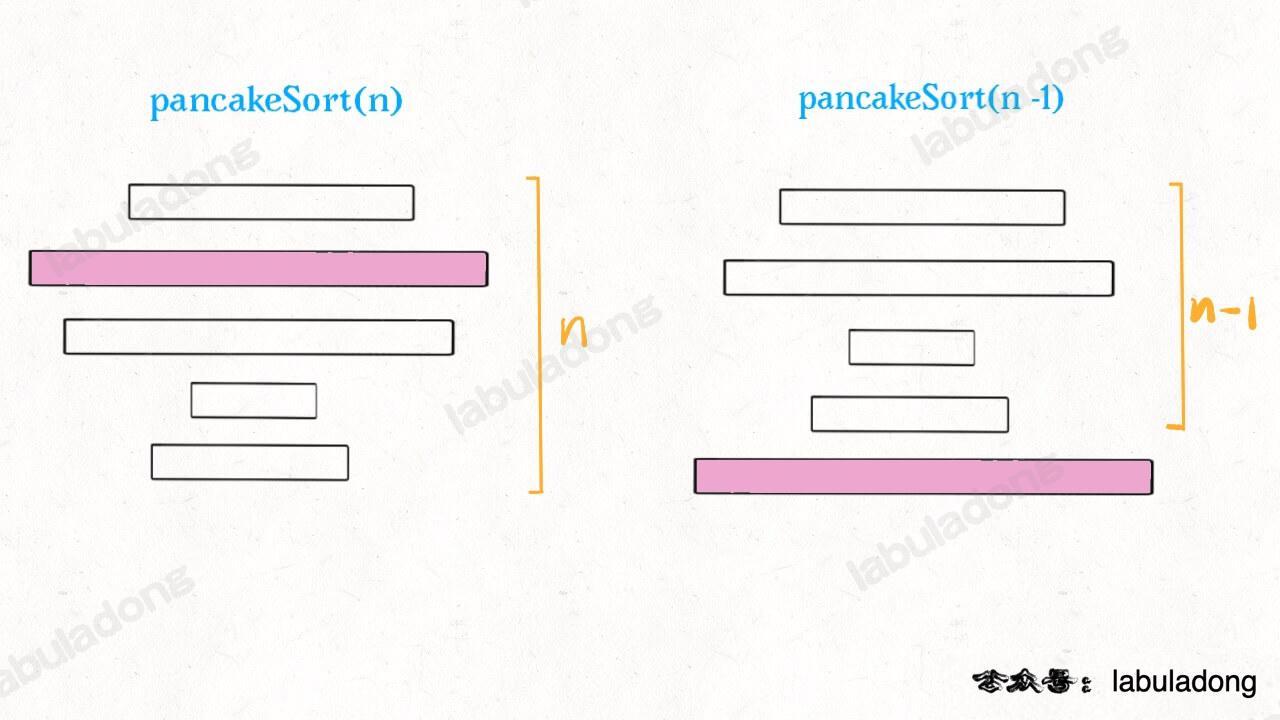
接下来,对于上面的这 n - 1 块饼,如何排序呢?还是先从中找到最大的一块饼,然后把这块饼放到底下,再递归调用 pancakeSort(A, n-1-1)……
你看,这就是递归性质,总结一下思路就是:
1、找到 n 个饼中最大的那个。
2、把这个最大的饼移到最底下。
3、递归调用 pancakeSort(A, n - 1)。
base case:n == 1 时,排序 1 个饼时不需要翻转。
那么,最后剩下个问题,如何设法将某块烧饼翻到最后呢?
其实很简单,比如第 3 块饼是最大的,我们想把它换到最后,也就是换到第 n 块。可以这样操作:
1、用锅铲将前 3 块饼翻转一下,这样最大的饼就翻到了最上面。
2、用锅铲将前 n 块饼全部翻转,这样最大的饼就翻到了第 n 块,也就是最后一块。
以上两个流程理解之后,基本就可以写出解法了,不过题目要求我们写出具体的反转操作序列,这也很简单,只要在每次翻转烧饼时记录下来就行了。
二、代码实现
只要把上述的思路用代码实现即可,唯一需要注意的是,数组索引从 0 开始,而我们要返回的结果是从 1 开始算的。
class Solution {
// 记录反转操作序列
LinkedList<Integer> res = new LinkedList<>();
List<Integer> pancakeSort(int[] cakes) {
sort(cakes, cakes.length);
return res;
}
void sort(int[] cakes, int n) {
// base case
if (n == 1) return;
// 寻找最大饼的索引
int maxCake = 0;
int maxCakeIndex = 0;
for (int i = 0; i < n; i++)
if (cakes[i] > maxCake) {
maxCakeIndex = i;
maxCake = cakes[i];
}
// 第一次翻转,将最大饼翻到最上面
reverse(cakes, 0, maxCakeIndex);
res.add(maxCakeIndex + 1);
// 第二次翻转,将最大饼翻到最下面
reverse(cakes, 0, n - 1);
res.add(n);
// 递归调用
sort(cakes, n - 1);
}
void reverse(int[] arr, int i, int j) {
while (i < j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
i++; j--;
}
}
}通过刚才的详细解释,这段代码应该是很清晰了。
算法的时间复杂度很容易计算,因为递归调用的次数是 n,每次递归调用都需要一次 for 循环,时间复杂度是 O(n),所以总的复杂度是 O(n^2)。
最后,我们可以思考一个问题:按照我们这个思路,得出的操作序列长度应该为 2(n - 1),因为每次递归都要进行 2 次翻转并记录操作,总共有 n 层递归,但由于 base case 直接返回结果,不进行翻转,所以最终的操作序列长度应该是固定的 2(n - 1)。
显然,这个结果不是最优的(最短的),比如说一堆煎饼 [3,2,4,1],我们的算法得到的翻转序列是 [3,4,2,3,1,2],但是最快捷的翻转方法应该是 [2,3,4]:
初始状态 :[3,2,4,1]
翻前 2 个:[2,3,4,1]
翻前 3 个:[4,3,2,1]
翻前 4 个:[1,2,3,4]
如果要求你的算法计算排序烧饼的最短操作序列,你该如何计算呢?或者说,解决这种求最优解法的问题,核心思路什么,一定需要使用什么算法技巧呢?
不妨分享一下你的思考。
_____________
《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复「全家桶」可下载配套 PDF 和刷题全家桶:

====其他语言代码====
python3
fengshuu 提供 Python3 解法代码:
class Solution:
# 记录反转操作序列
def __init__(self):
self.res = []
def pancakeSort(self, arr: List[int]) -> List[int]:
self.sort(arr, len(arr))
return self.res
def sort(self, cakes: List[int], n: int):
# base case
if 1 == n:
return
# 寻找最大饼的索引
max_cake_index = cakes[:n].index(n)
# 下面进行把最大的饼放到最后的两次翻转
# 如果最后一个饼就是最大的, 就不需要翻转, 直接进行下次递归
if max_cake_index != n - 1:
# 第一次翻转, 将最大饼翻到最上面
# 如果第一个饼本来就是最大的, 就不需要第一次翻转.
if max_cake_index != 0:
cakes[:max_cake_index + 1] = cakes[:max_cake_index + 1][::-1]
self.res.append(max_cake_index + 1)
# 第二次翻转,将最大饼翻到最下面
cakes[:n] = cakes[:n][::-1]
self.res.append(n)
# 递归调用
self.sort(cakes, n - 1)c++
fengshuu 提供 C++ 解法代码:
class Solution {
public:
vector<int> pancakeSort(vector<int>& arr) {
sort(arr, arr.size());
return res;
}
private:
// 记录反转操作序列
vector<int> res;
void sort(vector<int>& cakes, int n){
// base case
if(n == 1) return;
// 寻找最大饼的索引
int maxCakeIndex = max_element(cakes.begin(), cakes.begin() + n) - cakes.begin();
// 下面进行把最大的饼放到最后的两次翻转
// 如果最后一个饼就是最大的, 就不需要翻转, 直接进行下次递归
if (maxCakeIndex == n-1){
sort(cakes, n - 1);
return;
}
// 第一次翻转, 将最大饼翻到最上面
// 如果第一个饼本来就是最大的, 就不需要第一次翻转.
if (maxCakeIndex != 0) {
reverse(cakes.begin(), cakes.begin() + maxCakeIndex + 1);
res.push_back(maxCakeIndex + 1);
}
// 第二次翻转,将最大饼翻到最下面
reverse(cakes.begin(), cakes.begin() + n);
res.push_back(n);
// 递归调用
sort(cakes, n - 1);
}
};java
L-WEIWEI 提供 第969题的 Java 代码:
class Solution {
public List<Integer> pancakeSort(int[] A) {
List<Integer> ans = new ArrayList<Integer>();
int len = A.length;
if(len == 0){
return ans;
}
// maxIndex[0] == 当前轮次的最大元素, maxIndex[1] == 最大元素下标
int[] maxIndex = new int[2];
maxIndex[0] = Integer.MIN_VALUE;
int maxCount = 0;
// maxCount == len 时,说明完成了整个数组的最大值沉底操作,
while(maxCount < len - 1){
maxCount = maxValueDown(A, maxIndex, maxCount, ans);
// 每做完一次最大值沉底操作,初始化最大元素值
maxIndex[0] = Integer.MIN_VALUE;
}
return ans;
}
public int maxValueDown(int[] A, int[] maxIndex, int maxCount, List<Integer> ans){
// 遍历条件为 i < A.length - maxCount , 每次最大值沉底时,maxCount + 1,因此下次遍历即可不对最后 maxCount 个元素做操作
for(int i = 0; i < A.length - maxCount; i++){
// 元素大于当前储存的元素时,将值与下标 copy 到 maxIndex 数组中
if(A[i] > maxIndex[0]){
maxIndex[0] = A[i];
maxIndex[1] = i;
}
}
// 如果当前轮次最大元素的下标的下一位是上一轮次的最大下标,则不做翻转操作,直接返回 maxCount + 1
if(maxIndex[1] + 1 == A.length - maxCount){
return maxCount + 1;
}
// 使用最大值沉底时,当本轮最大值在首位时,不需要再将其先翻转至首位,所以不添加
if(maxIndex[1] > 0){
// 将该轮次要翻转的下标添加到结果集中,结果集中需要的是翻转的位置而不是下标,所以添加时下标得 + 1
ans.add(maxIndex[1] + 1);
}
// 双指针原地交换数组中的值
// 左指针指0
int left = 0;
// 右指针指向当前轮次最大元素的下标
int right = maxIndex[1];
while(left < right){
// 交换元素值
A[left] += A[right];
A[right] = A[left] - A[right];
A[left] -= A[right];
left++;
right--;
}
// 上面交换玩元素值后,当前轮次最大元素排在首位,再从上一轮次最大元素 - 1 的位置翻转
// 则当前轮次的最大元素成功沉底
ans.add(A.length - maxCount);
left = 0;
right = A.length - 1 - maxCount;
while(left < right){
A[left] += A[right];
A[right] = A[left] - A[right];
A[left] -= A[right];
left++;
right--;
}
return maxCount + 1;
}
}javascript
/**
* @param {number[]} arr
* @return {number[]}
*/
var pancakeSort = function (arr) {
let res = []
const sort = (cakes, n) => {
// base case
if (n === 1) return;
// 寻找最大饼的索引
let maxCake = 0;
let maxCakeIndex = 0;
for (let i = 0; i < n; i++)
if (cakes[i] > maxCake) {
maxCakeIndex = i;
maxCake = cakes[i];
}
// 第一次翻转,将最大饼翻到最上面
reverse(cakes, 0, maxCakeIndex);
res.push(maxCakeIndex + 1);
// 第二次翻转,将最大饼翻到最下面
reverse(cakes, 0, n - 1);
res.push(n);
// 递归调用
sort(cakes, n - 1);
}
let reverse = (arr, i, j) => {
while (i < j) {
let temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
i++;
j--;
}
}
sort(arr, arr.length)
return res;
};也可以写成下面这样。
var reserve = function (nums, k) {
let l = 0, r = k - 1
while (l < r) {
let temp = nums[l]
nums[l] = nums[r]
nums[r] = temp
l++
r--
}
}
/**
* @param {number[]} arr
* @return {number[]}
*/
var pancakeSort = function (arr) {
let n = arr.length
if (n === 0) return []
let nums = [...arr], ans = []
nums.sort((a, b) => a - b)
for (let i = n - 1, j = 0; i > -1; i--, j++) {
let index = arr.indexOf(nums[i])
ans.push(index + 1, n - j)
reserve(arr, index + 1)
reserve(arr, n - j)
}
return ans
};


