字符串乘法

通知:数据结构精品课 和 递归算法专题课 限时附赠网站会员,全新纸质书《labuladong 的算法笔记》 出版,签名版限时半价!另外,建议你在我的 网站 学习文章,体验更好。
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
| LeetCode | 力扣 | 难度 |
|---|---|---|
| 43. Multiply Strings | 43. 字符串相乘 | 🟠 |
-----------
对于比较小的数字,做运算可以直接使用编程语言提供的运算符,但是如果相乘的两个因数非常大,语言提供的数据类型可能就会溢出。一种替代方案就是,运算数以字符串的形式输入,然后模仿我们小学学习的乘法算术过程计算出结果,并且也用字符串表示。
看下力扣第 43 题「字符串相乘」:
需要注意的是,num1 和 num2 可以非常长,所以不可以把他们直接转成整型然后运算,唯一的思路就是模仿我们手算乘法。
比如说我们手算 123 × 45,应该会这样计算:

计算 123 × 5,再计算 123 × 4,最后错一位相加。这个流程恐怕小学生都可以熟练完成,但是你是否能把这个运算过程进一步机械化,写成一套算法指令让没有任何智商的计算机来执行呢?
你看这个简单过程,其中涉及乘法进位,涉及错位相加,还涉及加法进位;而且还有一些不易察觉的问题,比如说两位数乘以两位数,结果可能是四位数,也可能是三位数,你怎么想出一个标准化的处理方式?这就是算法的魅力,如果没有计算机思维,简单的问题可能都没办法自动化处理。
首先,我们这种手算方式还是太「高级」了,我们要再「低级」一点,123 × 5 和 123 × 4 的过程还可以进一步分解,最后再相加:
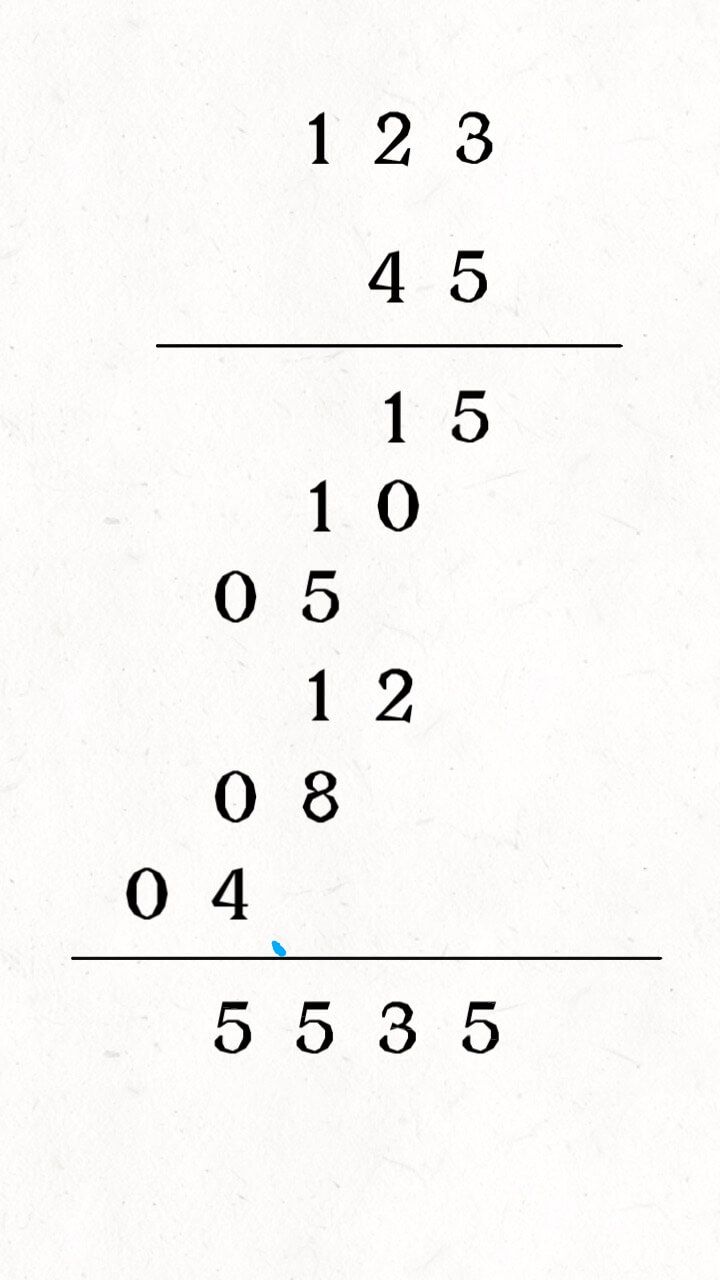
现在 123 并不大,如果是个很大的数字的话,是无法直接计算乘积的。我们可以用一个数组在底下接收相加结果:
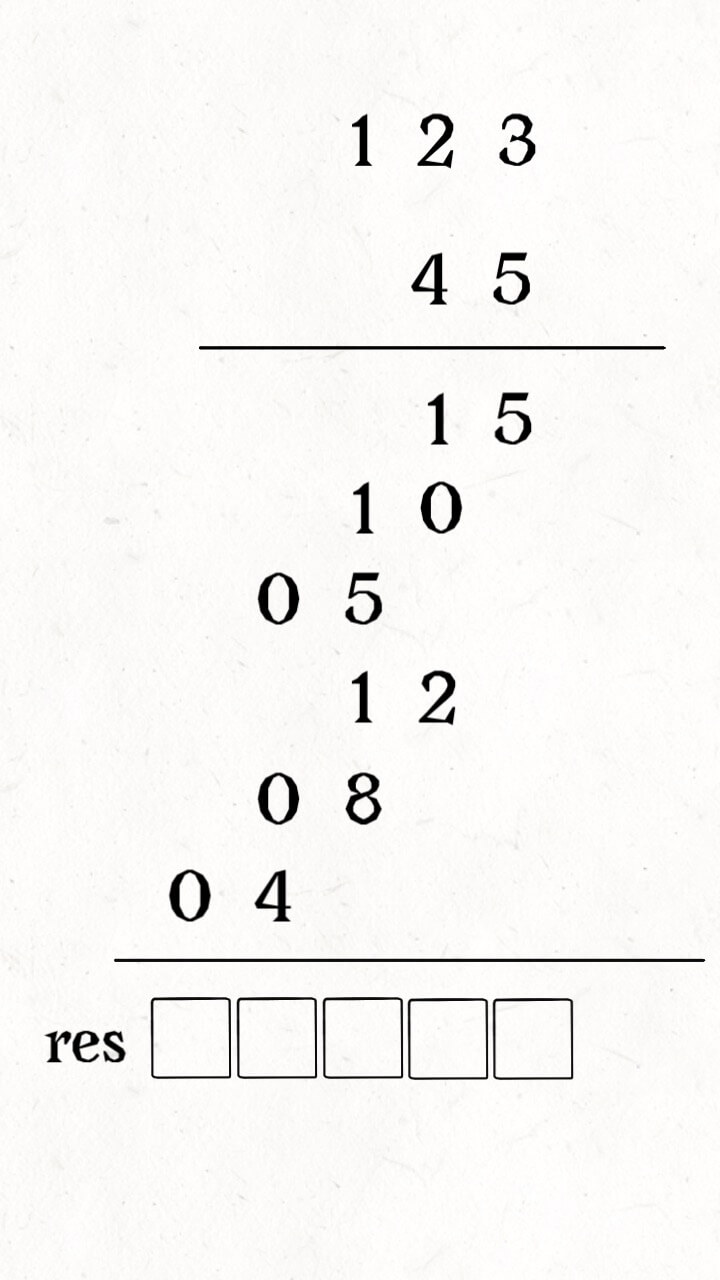
整个计算过程大概是这样,有两个指针 i,j 在 num1 和 num2 上游走,计算乘积,同时将乘积叠加到 res 的正确位置,如下 GIF 图所示:
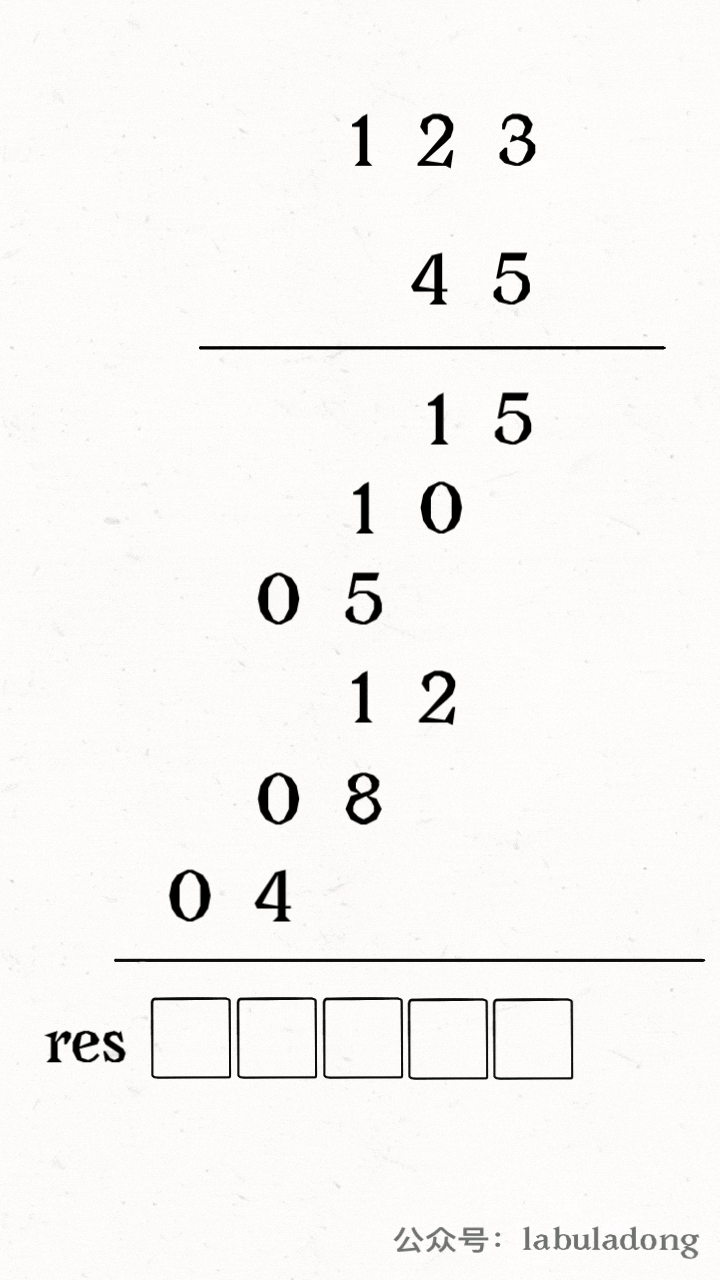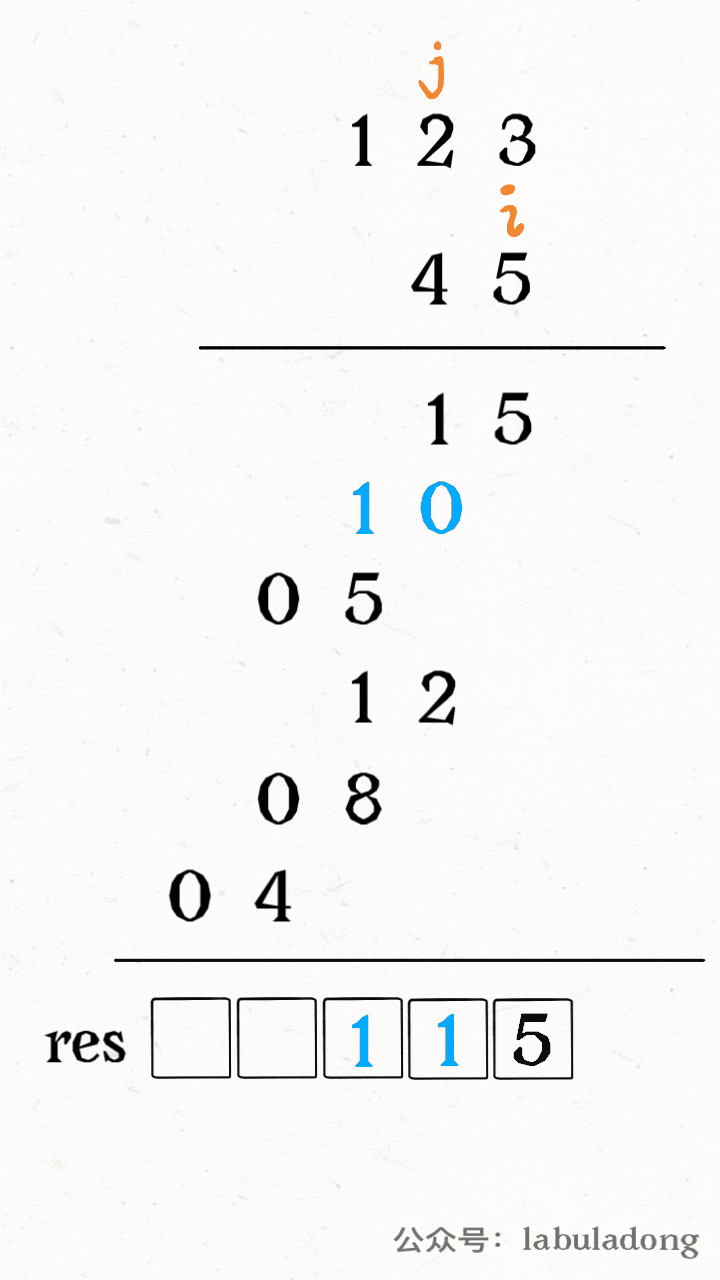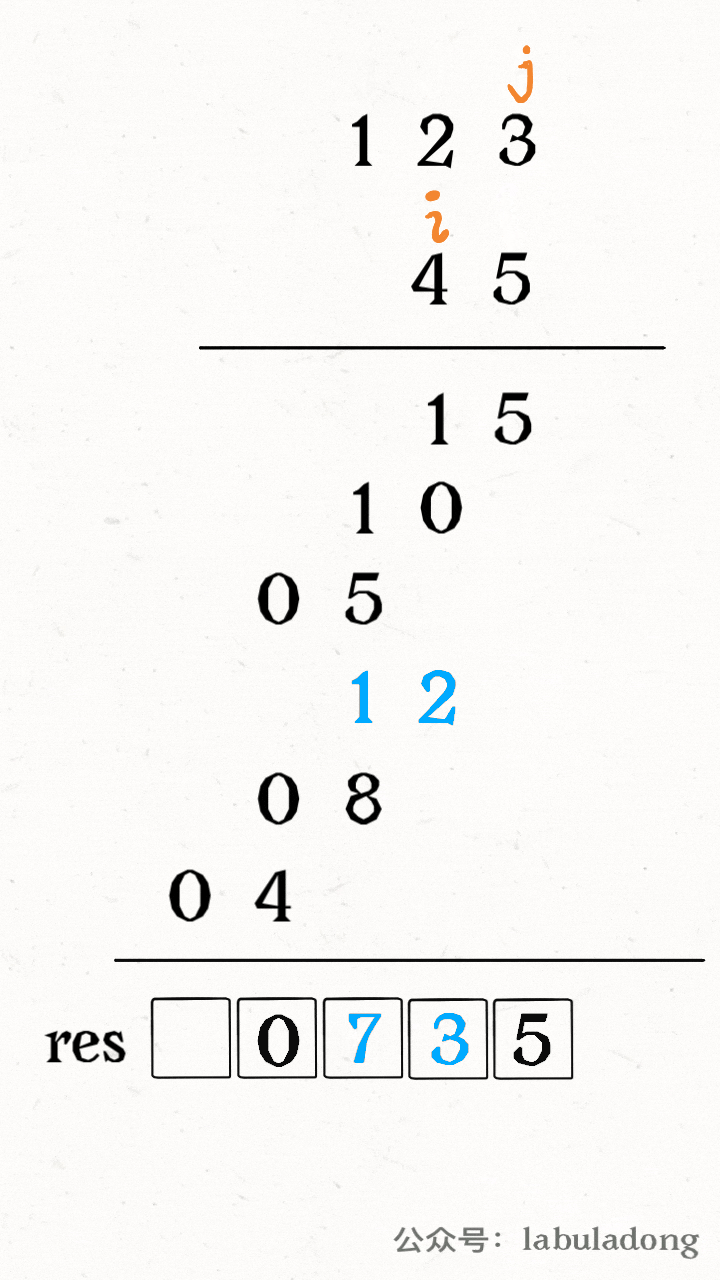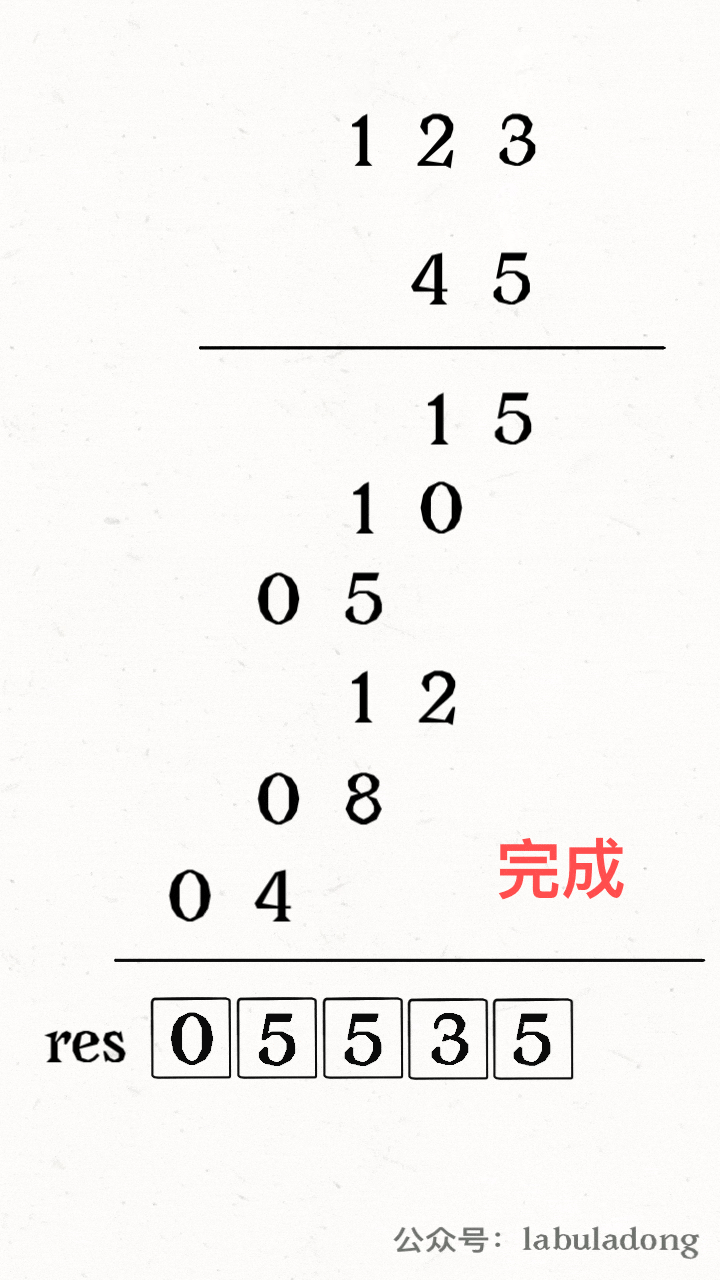
现在还有一个关键问题,如何将乘积叠加到 res 的正确位置,或者说,如何通过 i,j 计算 res 的对应索引呢?
其实,细心观察之后就发现,num1[i] 和 num2[j] 的乘积对应的就是 res[i+j] 和 res[i+j+1] 这两个位置。

明白了这一点,就可以用代码模仿出这个计算过程了:
string multiply(string num1, string num2) {
int m = num1.size(), n = num2.size();
// 结果最多为 m + n 位数
vector<int> res(m + n, 0);
// 从个位数开始逐位相乘
for (int i = m - 1; i >= 0; i--)
for (int j = n - 1; j >= 0; j--) {
int mul = (num1[i]-'0') * (num2[j]-'0');
// 乘积在 res 对应的索引位置
int p1 = i + j, p2 = i + j + 1;
// 叠加到 res 上
int sum = mul + res[p2];
res[p2] = sum % 10;
res[p1] += sum / 10;
}
// 结果前缀可能存的 0(未使用的位)
int i = 0;
while (i < res.size() && res[i] == 0)
i++;
// 将计算结果转化成字符串
string str;
for (; i < res.size(); i++)
str.push_back('0' + res[i]);
return str.size() == 0 ? "0" : str;
}至此,字符串乘法算法就完成了。
总结一下,我们习以为常的一些思维方式,在计算机看来是非常难以做到的。比如说我们习惯的算术流程并不复杂,但是如果让你再进一步,翻译成代码逻辑,并不简单。算法需要将计算流程再简化,通过边算边叠加的方式来得到结果。
俗话教育我们,不要陷入思维定式,不要程序化,要发散思维,要创新。但我觉得程序化并不是坏事,可以大幅提高效率,减小失误率。算法不就是一套程序化的思维吗,只有程序化才能让计算机帮助我们解决复杂问题呀!
也许算法就是一种寻找思维定式的思维吧,希望本文对你有帮助。
_____________
《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复「全家桶」可下载配套 PDF 和刷题全家桶:

====其他语言代码====
python
fengshuu 提供 Python 解法代码:
def multiply(num1: str, num2: str) -> str:
m, n = len(num1), len(num2)
# 结果最多为 m + n 位数
res = [0] * (m + n)
# 从个位数开始逐位相乘
for i in range(m-1, -1, -1):
for j in range(n-1, -1, -1):
mul = int(num1[i]) * int(num2[j])
# 乘积在 res 对应的索引位置
p1 = i + j
p2 = i + j + 1
# 叠加到 res 上
digit_sum = mul + res[p2]
res[p2] = digit_sum % 10
res[p1] += digit_sum // 10
# 结果前缀可能存的 0(未使用的位)
i = 0
while i < len(res) and res[i] == 0:
i += 1
# 将计算结果转化成字符串
result_str = "".join(str(x) for x in res[i:])
return "0" if len(result_str) == 0 else result_strjava
Zane Wang 提供 Java 解法代码:
public String multiply(String num1, String num2) {
// 初始化字符数组
char[] s1 = num1.toCharArray();
char[] s2 = num2.toCharArray();
// 结果长度最多为两字符串长度之和
int[] res = new int[s1.length + s2.length];
// 从个位开始遍历,把两数字中每一位相乘
for (int i = s1.length - 1; i >= 0; i--) {
for (int j = s2.length - 1; j >= 0; j--) {
// 计算乘积,并把乘积放在 res 对应的位置, 暂时不考虑进位
res[i + j + 1] += (s1[i] - '0') * (s2[j] - '0');
}
}
// 从个位再次遍历,如果上一次遍历中两数乘积为两位数,进位并叠加到前面一位
int carry = 0;
for (int i = res.length - 1; i >= 0; i--) {
int sum = res[i] + carry;
res[i] = sum % 10;
carry = sum / 10;
}
//遍历res数组,构造最终答案字符串
StringBuilder ans = new StringBuilder();
int i = 0;
// 首先找到不为0的第一位
while (i < res.length - 1 && res[i] == 0) {
i++;
}
// 将后面的数字附加到ans后面
while (i < res.length) {
ans.append(res[i++]);
}
return ans.toString();
}javascript
/**
* @param {string} num1
* @param {string} num2
* @return {string}
*/
const multiply = (num1, num2) => {
const m = num1.length;
const n = num2.length;
const pos = new Array(m + n).fill(0);
for (let i = m - 1; i >= 0; i--) {
const n1 = +num1[i];
for (let j = n - 1; j >= 0; j--) {
const n2 = +num2[j];
const multi = n1 * n2;
const sum = pos[i + j + 1] + multi;
pos[i + j + 1] = sum % 10;
pos[i + j] += sum / 10 | 0;
}
}
while (pos[0] === 0) {
pos.shift();
}
return pos.length ? pos.join('') : '0';
};


