图论算法基础

通知:数据结构精品课 和 递归算法专题课 限时附赠网站会员,全新纸质书《labuladong 的算法笔记》 出版,签名版限时半价!另外,建议你在我的 网站 学习文章,体验更好。
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
-----------
tip:本文有视频版:图论基础及遍历算法。建议关注我的 B 站账号,我会用视频领读的方式带大家学习那些稍有难度的算法技巧。
经常有读者问我「图」这种数据结构,其实我在 学习数据结构和算法的框架思维 中说过,虽然图可以玩出更多的算法,解决更复杂的问题,但本质上图可以认为是多叉树的延伸。
面试笔试很少出现图相关的问题,就算有,大多也是简单的遍历问题,基本上可以完全照搬多叉树的遍历。
那么,本文依然秉持我们号的风格,只讲「图」最实用的,离我们最近的部分,让你心里对图有个直观的认识,文末我给出了其他经典图论算法,理解本文后应该都可以拿下的。
图的逻辑结构和具体实现
一幅图是由节点和边构成的,逻辑结构如下:
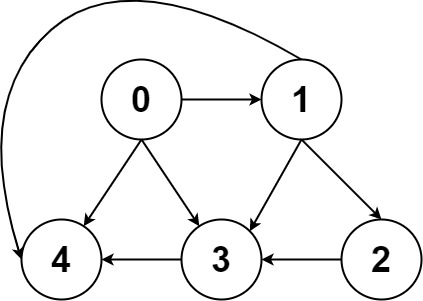
什么叫「逻辑结构」?就是说为了方便研究,我们把图抽象成这个样子。
根据这个逻辑结构,我们可以认为每个节点的实现如下:
/* 图节点的逻辑结构 */
class Vertex {
int id;
Vertex[] neighbors;
}看到这个实现,你有没有很熟悉?它和我们之前说的多叉树节点几乎完全一样:
/* 基本的 N 叉树节点 */
class TreeNode {
int val;
TreeNode[] children;
}所以说,图真的没啥高深的,本质上就是个高级点的多叉树而已,适用于树的 DFS/BFS 遍历算法,全部适用于图。
不过呢,上面的这种实现是「逻辑上的」,实际上我们很少用这个 Vertex 类实现图,而是用常说的邻接表和邻接矩阵来实现。
比如还是刚才那幅图:

用邻接表和邻接矩阵的存储方式如下:
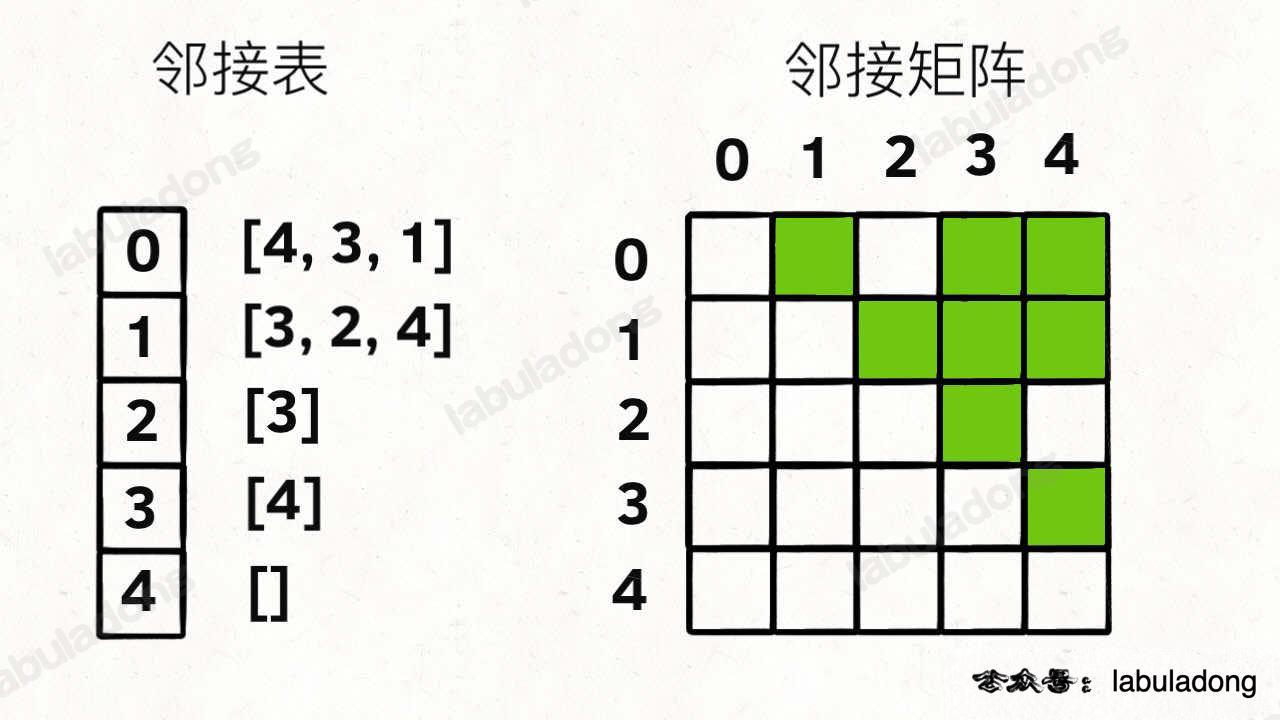
邻接表很直观,我把每个节点 x 的邻居都存到一个列表里,然后把 x 和这个列表关联起来,这样就可以通过一个节点 x 找到它的所有相邻节点。
邻接矩阵则是一个二维布尔数组,我们权且称为 matrix,如果节点 x 和 y 是相连的,那么就把 matrix[x][y] 设为 true(上图中绿色的方格代表 true)。如果想找节点 x 的邻居,去扫一圈 matrix[x][..] 就行了。
如果用代码的形式来表现,邻接表和邻接矩阵大概长这样:
// 邻接表
// graph[x] 存储 x 的所有邻居节点
List<Integer>[] graph;
// 邻接矩阵
// matrix[x][y] 记录 x 是否有一条指向 y 的边
boolean[][] matrix;那么,为什么有这两种存储图的方式呢?肯定是因为他们各有优劣。
对于邻接表,好处是占用的空间少。
你看邻接矩阵里面空着那么多位置,肯定需要更多的存储空间。
但是,邻接表无法快速判断两个节点是否相邻。
比如说我想判断节点 1 是否和节点 3 相邻,我要去邻接表里 1 对应的邻居列表里查找 3 是否存在。但对于邻接矩阵就简单了,只要看看 matrix[1][3] 就知道了,效率高。
所以说,使用哪一种方式实现图,要看具体情况。
tip:在常规的算法题中,邻接表的使用会更频繁一些,主要是因为操作起来较为简单,但这不意味着邻接矩阵应该被轻视。矩阵是一个强有力的数学工具,图的一些隐晦性质可以借助精妙的矩阵运算展现出来。不过本文不准备引入数学内容,所以有兴趣的读者可以自行搜索学习。
最后,我们再明确一个图论中特有的度(degree)的概念,在无向图中,「度」就是每个节点相连的边的条数。
由于有向图的边有方向,所以有向图中每个节点「度」被细分为入度(indegree)和出度(outdegree),比如下图:

其中节点 3 的入度为 3(有三条边指向它),出度为 1(它有 1 条边指向别的节点)。
好了,对于「图」这种数据结构,能看懂上面这些就绰绰够用了。
那你可能会问,我们上面说的这个图的模型仅仅是「有向无权图」,不是还有什么加权图,无向图,等等……
其实,这些更复杂的模型都是基于这个最简单的图衍生出来的。
有向加权图怎么实现?很简单呀:
如果是邻接表,我们不仅仅存储某个节点 x 的所有邻居节点,还存储 x 到每个邻居的权重,不就实现加权有向图了吗?
如果是邻接矩阵,matrix[x][y] 不再是布尔值,而是一个 int 值,0 表示没有连接,其他值表示权重,不就变成加权有向图了吗?
如果用代码的形式来表现,大概长这样:
// 邻接表
// graph[x] 存储 x 的所有邻居节点以及对应的权重
List<int[]>[] graph;
// 邻接矩阵
// matrix[x][y] 记录 x 指向 y 的边的权重,0 表示不相邻
int[][] matrix;无向图怎么实现?也很简单,所谓的「无向」,是不是等同于「双向」?
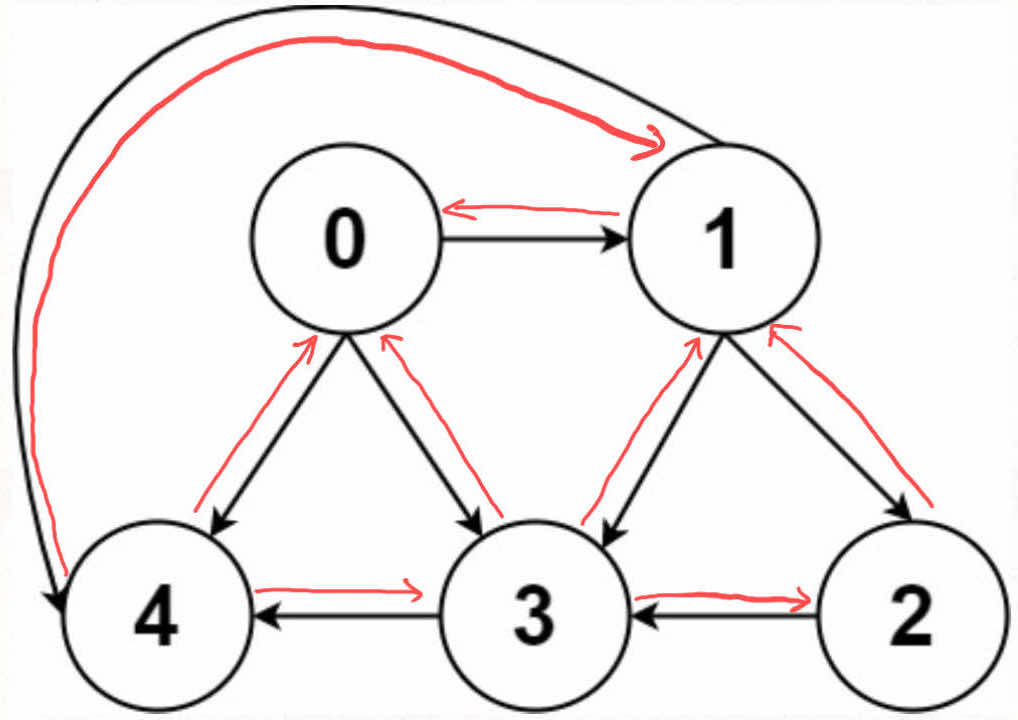
如果连接无向图中的节点 x 和 y,把 matrix[x][y] 和 matrix[y][x] 都变成 true 不就行了;邻接表也是类似的操作,在 x 的邻居列表里添加 y,同时在 y 的邻居列表里添加 x。
把上面的技巧合起来,就变成了无向加权图……
好了,关于图的基本介绍就到这里,现在不管来什么乱七八糟的图,你心里应该都有底了。
下面来看看所有数据结构都逃不过的问题:遍历。
图的遍历
学习数据结构和算法的框架思维 说过,各种数据结构被发明出来无非就是为了遍历和访问,所以「遍历」是所有数据结构的基础。
图怎么遍历?还是那句话,参考多叉树,多叉树的 DFS 遍历框架如下:
/* 多叉树遍历框架 */
void traverse(TreeNode root) {
if (root == null) return;
// 前序位置
for (TreeNode child : root.children) {
traverse(child);
}
// 后序位置
}图和多叉树最大的区别是,图是可能包含环的,你从图的某一个节点开始遍历,有可能走了一圈又回到这个节点,而树不会出现这种情况,从某个节点出发必然走到叶子节点,绝不可能回到它自身。
所以,如果图包含环,遍历框架就要一个 visited 数组进行辅助:
// 记录被遍历过的节点
boolean[] visited;
// 记录从起点到当前节点的路径
boolean[] onPath;
/* 图遍历框架 */
void traverse(Graph graph, int s) {
if (visited[s]) return;
// 经过节点 s,标记为已遍历
visited[s] = true;
// 做选择:标记节点 s 在路径上
onPath[s] = true;
for (int neighbor : graph.neighbors(s)) {
traverse(graph, neighbor);
}
// 撤销选择:节点 s 离开路径
onPath[s] = false;
}注意 visited 数组和 onPath 数组的区别,因为二叉树算是特殊的图,所以用遍历二叉树的过程来理解下这两个数组的区别:
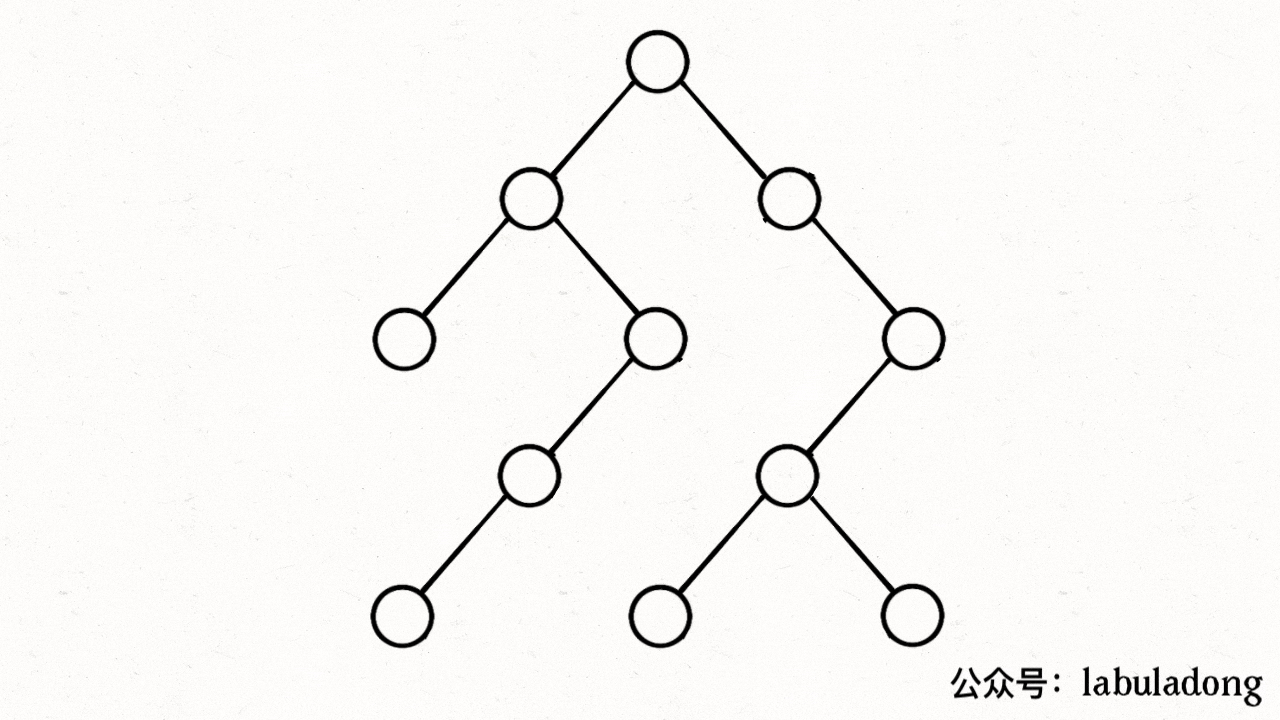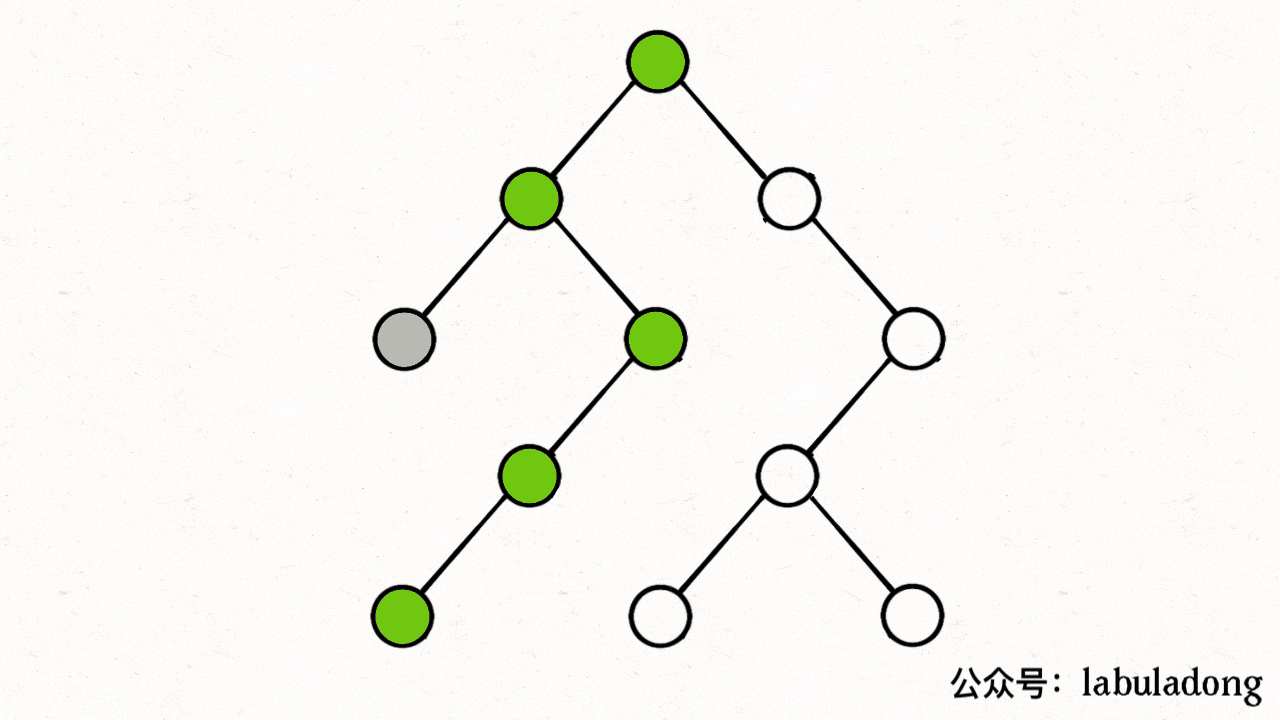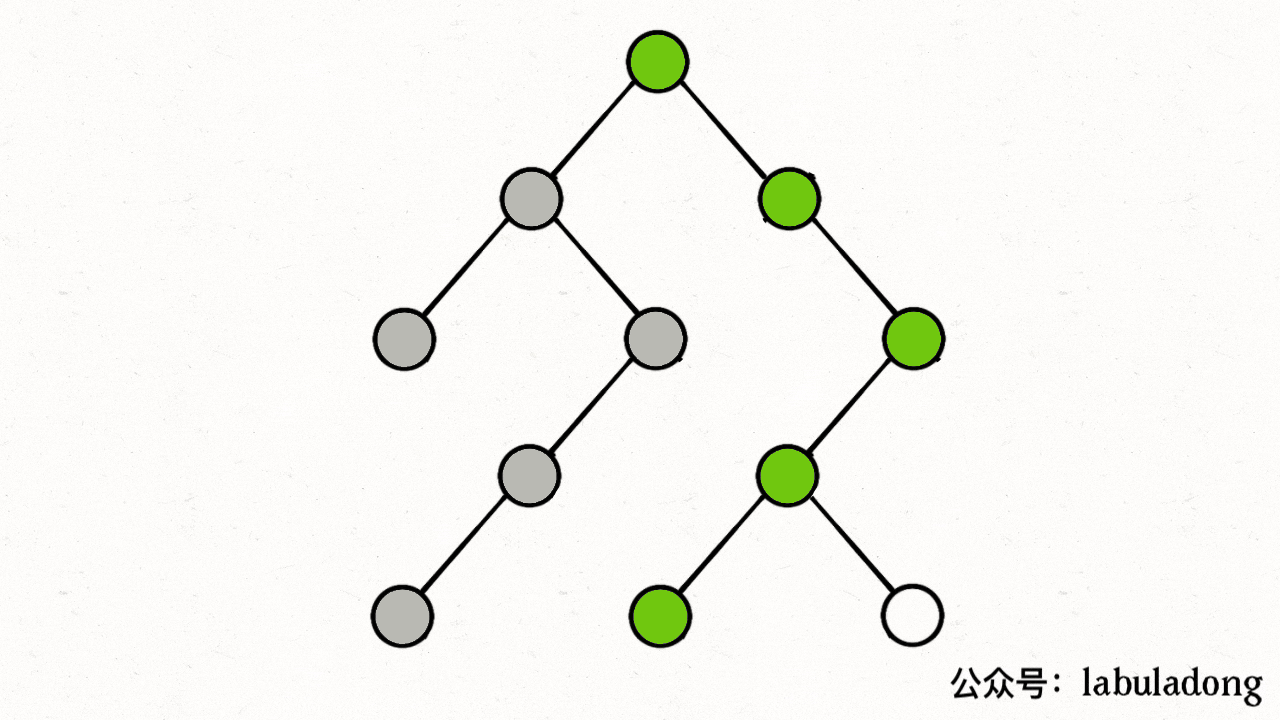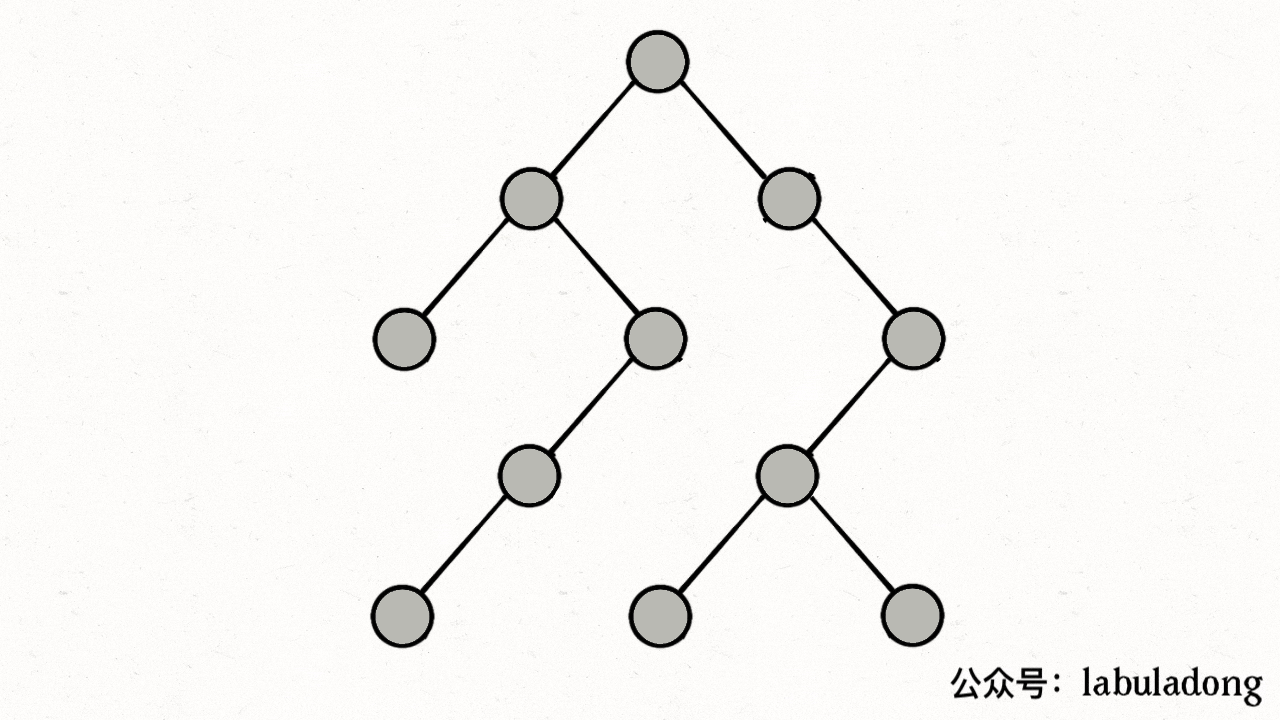
上述 GIF 描述了递归遍历二叉树的过程,在 visited 中被标记为 true 的节点用灰色表示,在 onPath 中被标记为 true 的节点用绿色表示,类比贪吃蛇游戏,visited 记录蛇经过过的格子,而 onPath 仅仅记录蛇身。在图的遍历过程中,onPath 用于判断是否成环,类比当贪吃蛇自己咬到自己(成环)的场景,这下你可以理解它们二者的区别了吧。
如果让你处理路径相关的问题,这个 onPath 变量是肯定会被用到的,比如 拓扑排序 中就有运用。
另外,你应该注意到了,这个 onPath 数组的操作很像前文 回溯算法核心套路 中做「做选择」和「撤销选择」,区别在于位置:回溯算法的「做选择」和「撤销选择」在 for 循环里面,而对 onPath 数组的操作在 for 循环外面。
为什么有这个区别呢?这就是前文 东哥带你刷二叉树(纲领篇) 中讲到的回溯算法和 DFS 算法的区别所在:回溯算法关注的不是节点,而是树枝。如果没印象了,强烈建议重新阅读前文。
对于回溯算法,我们需要在「树枝」上做选择和撤销选择:
![]()
他们的区别可以这样反应到代码上:
// DFS 算法,关注点在节点
void traverse(TreeNode root) {
if (root == null) return;
printf("进入节点 %s", root);
for (TreeNode child : root.children) {
traverse(child);
}
printf("离开节点 %s", root);
}
// 回溯算法,关注点在树枝
void backtrack(TreeNode root) {
if (root == null) return;
for (TreeNode child : root.children) {
// 做选择
printf("从 %s 到 %s", root, child);
backtrack(child);
// 撤销选择
printf("从 %s 到 %s", child, root);
}
}如果执行这段代码,你会发现根节点被漏掉了:
void traverse(TreeNode root) {
if (root == null) return;
for (TreeNode child : root.children) {
printf("进入节点 %s", child);
traverse(child);
printf("离开节点 %s", child);
}
}所以对于这里「图」的遍历,我们应该用 DFS 算法,即把 onPath 的操作放到 for 循环外面,否则会漏掉记录起始点的遍历。
说了这么多 onPath 数组,再说下 visited 数组,其目的很明显了,由于图可能含有环,visited 数组就是防止递归重复遍历同一个节点进入死循环的。
当然,如果题目告诉你图中不含环,可以把 visited 数组都省掉,基本就是多叉树的遍历。
题目实践
下面我们来看力扣第 797 题「所有可能路径」,函数签名如下:
List<List<Integer>> allPathsSourceTarget(int[][] graph);题目输入一幅有向无环图,这个图包含 n 个节点,标号为 0, 1, 2,..., n - 1,请你计算所有从节点 0 到节点 n - 1 的路径。
输入的这个 graph 其实就是「邻接表」表示的一幅图,graph[i] 存储这节点 i 的所有邻居节点。
比如输入 graph = [[1,2],[3],[3],[]],就代表下面这幅图:
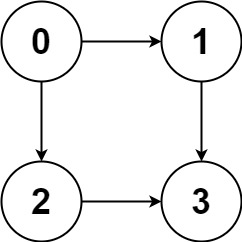
算法应该返回 [[0,1,3],[0,2,3]],即 0 到 3 的所有路径。
解法很简单,以 0 为起点遍历图,同时记录遍历过的路径,当遍历到终点时将路径记录下来即可。
既然输入的图是无环的,我们就不需要 visited 数组辅助了,直接套用图的遍历框架:
class Solution {
// 记录所有路径
List<List<Integer>> res = new LinkedList<>();
public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
// 维护递归过程中经过的路径
LinkedList<Integer> path = new LinkedList<>();
traverse(graph, 0, path);
return res;
}
/* 图的遍历框架 */
void traverse(int[][] graph, int s, LinkedList<Integer> path) {
// 添加节点 s 到路径
path.addLast(s);
int n = graph.length;
if (s == n - 1) {
// 到达终点
res.add(new LinkedList<>(path));
// 可以在这直接 return,但要 removeLast 正确维护 path
// path.removeLast();
// return;
// 不 return 也可以,因为图中不包含环,不会出现无限递归
}
// 递归每个相邻节点
for (int v : graph[s]) {
traverse(graph, v, path);
}
// 从路径移出节点 s
path.removeLast();
}
}这道题就这样解决了,注意 Java 的语言特性,因为 Java 函数参数传的是对象引用,所以向 res 中添加 path 时需要拷贝一个新的列表,否则最终 res 中的列表都是空的。
最后总结一下,图的存储方式主要有邻接表和邻接矩阵,无论什么花里胡哨的图,都可以用这两种方式存储。
在笔试中,最常考的算法是图的遍历,和多叉树的遍历框架是非常类似的。
当然,图还会有很多其他的有趣算法,比如 二分图判定,环检测和拓扑排序(编译器循环引用检测就是类似的算法),最小生成树,Dijkstra 最短路径算法 等等,有兴趣的读者可以去看看,本文就到这了。
引用本文的文章
引用本文的题目
安装 我的 Chrome 刷题插件 点开下列题目可直接查看解题思路:
_____________
《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复「全家桶」可下载配套 PDF 和刷题全家桶:




