特殊数据结构:单调栈

通知:数据结构精品课 和 递归算法专题课 限时附赠网站会员,全新纸质书《labuladong 的算法笔记》 出版,签名版限时半价!另外,建议你在我的 网站 学习文章,体验更好。
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
| LeetCode | 力扣 | 难度 |
|---|---|---|
| 496. Next Greater Element I | 496. 下一个更大元素 I | 🟢 |
| 503. Next Greater Element II | 503. 下一个更大元素 II | 🟠 |
| 739. Daily Temperatures | 739. 每日温度 | 🟠 |
| - | 剑指 Offer II 038. 每日温度 | 🟠 |
-----------
栈(stack)是很简单的一种数据结构,先进后出的逻辑顺序,符合某些问题的特点,比如说函数调用栈。单调栈实际上就是栈,只是利用了一些巧妙的逻辑,使得每次新元素入栈后,栈内的元素都保持有序(单调递增或单调递减)。
听起来有点像堆(heap)?不是的,单调栈用途不太广泛,只处理一类典型的问题,比如「下一个更大元素」,「上一个更小元素」等。本文用讲解单调队列的算法模版解决「下一个更大元素」相关问题,并且探讨处理「循环数组」的策略。至于其他的变体和经典例题,我会在 数据结构精品课 中讲解。
单调栈模板
现在给你出这么一道题:输入一个数组 nums,请你返回一个等长的结果数组,结果数组中对应索引存储着下一个更大元素,如果没有更大的元素,就存 -1。函数签名如下:
int[] nextGreaterElement(int[] nums);比如说,输入一个数组 nums = [2,1,2,4,3],你返回数组 [4,2,4,-1,-1]。因为第一个 2 后面比 2 大的数是 4; 1 后面比 1 大的数是 2;第二个 2 后面比 2 大的数是 4; 4 后面没有比 4 大的数,填 -1;3 后面没有比 3 大的数,填 -1。
这道题的暴力解法很好想到,就是对每个元素后面都进行扫描,找到第一个更大的元素就行了。但是暴力解法的时间复杂度是 O(n^2)。
这个问题可以这样抽象思考:把数组的元素想象成并列站立的人,元素大小想象成人的身高。这些人面对你站成一列,如何求元素「2」的下一个更大元素呢?很简单,如果能够看到元素「2」,那么他后面可见的第一个人就是「2」的下一个更大元素,因为比「2」小的元素身高不够,都被「2」挡住了,第一个露出来的就是答案。
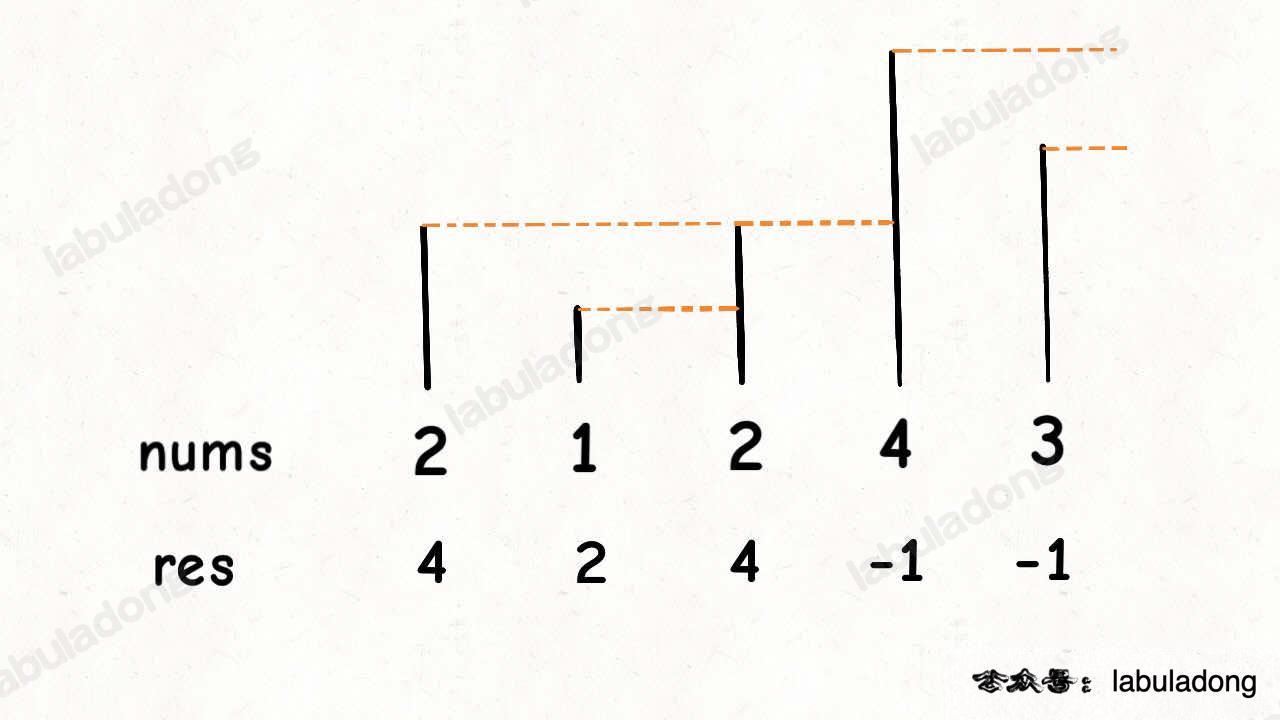
这个情景很好理解吧?带着这个抽象的情景,先来看下代码。
int[] nextGreaterElement(int[] nums) {
int n = nums.length;
// 存放答案的数组
int[] res = new int[n];
Stack<Integer> s = new Stack<>();
// 倒着往栈里放
for (int i = n - 1; i >= 0; i--) {
// 判定个子高矮
while (!s.isEmpty() && s.peek() <= nums[i]) {
// 矮个起开,反正也被挡着了。。。
s.pop();
}
// nums[i] 身后的更大元素
res[i] = s.isEmpty() ? -1 : s.peek();
s.push(nums[i]);
}
return res;
}这就是单调队列解决问题的模板。for 循环要从后往前扫描元素,因为我们借助的是栈的结构,倒着入栈,其实是正着出栈。while 循环是把两个「个子高」元素之间的元素排除,因为他们的存在没有意义,前面挡着个「更高」的元素,所以他们不可能被作为后续进来的元素的下一个更大元素了。
这个算法的时间复杂度不是那么直观,如果你看到 for 循环嵌套 while 循环,可能认为这个算法的复杂度也是 O(n^2),但是实际上这个算法的复杂度只有 O(n)。
分析它的时间复杂度,要从整体来看:总共有 n 个元素,每个元素都被 push 入栈了一次,而最多会被 pop 一次,没有任何冗余操作。所以总的计算规模是和元素规模 n 成正比的,也就是 O(n) 的复杂度。
问题变形
单调栈的使用技巧差不多了,首先来一个简单的变形,力扣第 496 题「下一个更大元素 I」:
这道题给你输入两个数组 nums1 和 nums2,让你求 nums1 中的元素在 nums2 中的下一个更大元素,函数签名如下:
int[] nextGreaterElement(int[] nums1, int[] nums2)其实和把我们刚才的代码改一改就可以解决这道题了,因为题目说 nums1 是 nums2 的子集,那么我们先把 nums2 中每个元素的下一个更大元素算出来存到一个映射里,然后再让 nums1 中的元素去查表即可:
int[] nextGreaterElement(int[] nums1, int[] nums2) {
// 记录 nums2 中每个元素的下一个更大元素
int[] greater = nextGreaterElement(nums2);
// 转化成映射:元素 x -> x 的下一个最大元素
HashMap<Integer, Integer> greaterMap = new HashMap<>();
for (int i = 0; i < nums2.length; i++) {
greaterMap.put(nums2[i], greater[i]);
}
// nums1 是 nums2 的子集,所以根据 greaterMap 可以得到结果
int[] res = new int[nums1.length];
for (int i = 0; i < nums1.length; i++) {
res[i] = greaterMap.get(nums1[i]);
}
return res;
}
int[] nextGreaterElement(int[] nums) {
// 见上文
}再看看力扣第 739 题「每日温度」:
给你一个数组 temperatures,这个数组存放的是近几天的天气气温,你返回一个等长的数组,计算:对于每一天,你还要至少等多少天才能等到一个更暖和的气温;如果等不到那一天,填 0。函数签名如下:
int[] dailyTemperatures(int[] temperatures);比如说给你输入 temperatures = [73,74,75,71,69,76],你返回 [1,1,3,2,1,0]。因为第一天 73 华氏度,第二天 74 华氏度,比 73 大,所以对于第一天,只要等一天就能等到一个更暖和的气温,后面的同理。
这个问题本质上也是找下一个更大元素,只不过现在不是问你下一个更大元素的值是多少,而是问你当前元素距离下一个更大元素的索引距离而已。
相同的思路,直接调用单调栈的算法模板,稍作改动就可以,直接上代码吧:
int[] dailyTemperatures(int[] temperatures) {
int n = temperatures.length;
int[] res = new int[n];
// 这里放元素索引,而不是元素
Stack<Integer> s = new Stack<>();
/* 单调栈模板 */
for (int i = n - 1; i >= 0; i--) {
while (!s.isEmpty() && temperatures[s.peek()] <= temperatures[i]) {
s.pop();
}
// 得到索引间距
res[i] = s.isEmpty() ? 0 : (s.peek() - i);
// 将索引入栈,而不是元素
s.push(i);
}
return res;
}单调栈讲解完毕,下面开始另一个重点:如何处理「循环数组」。
如何处理环形数组
同样是求下一个更大元素,现在假设给你的数组是个环形的,如何处理?力扣第 503 题「下一个更大元素 II」就是这个问题:输入一个「环形数组」,请你计算其中每个元素的下一个更大元素。
比如输入 [2,1,2,4,3],你应该返回 [4,2,4,-1,4],因为拥有了环形属性,最后一个元素 3 绕了一圈后找到了比自己大的元素 4。
我们一般是通过 % 运算符求模(余数),来模拟环形特效:
int[] arr = {1,2,3,4,5};
int n = arr.length, index = 0;
while (true) {
// 在环形数组中转圈
print(arr[index % n]);
index++;
}这个问题肯定还是要用单调栈的解题模板,但难点在于,比如输入是 [2,1,2,4,3],对于最后一个元素 3,如何找到元素 4 作为下一个更大元素。
对于这种需求,常用套路就是将数组长度翻倍:
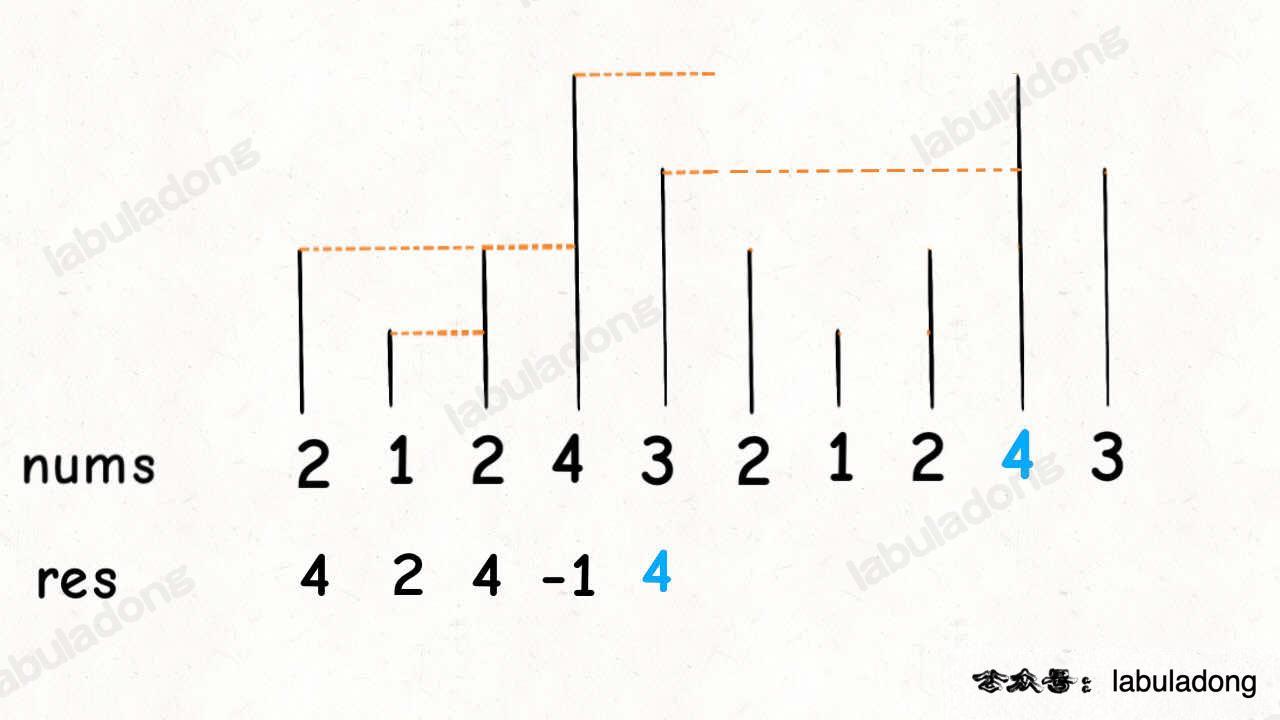
这样,元素 3 就可以找到元素 4 作为下一个更大元素了,而且其他的元素都可以被正确地计算。
有了思路,最简单的实现方式当然可以把这个双倍长度的数组构造出来,然后套用算法模板。但是,我们可以不用构造新数组,而是利用循环数组的技巧来模拟数组长度翻倍的效果。直接看代码吧:
int[] nextGreaterElements(int[] nums) {
int n = nums.length;
int[] res = new int[n];
Stack<Integer> s = new Stack<>();
// 数组长度加倍模拟环形数组
for (int i = 2 * n - 1; i >= 0; i--) {
// 索引 i 要求模,其他的和模板一样
while (!s.isEmpty() && s.peek() <= nums[i % n]) {
s.pop();
}
res[i % n] = s.isEmpty() ? -1 : s.peek();
s.push(nums[i % n]);
}
return res;
}这样,就可以巧妙解决环形数组的问题,时间复杂度 O(N)。
最后提出一些问题吧,本文提供的单调栈模板是 nextGreaterElement 函数,可以计算每个元素的下一个更大元素,但如果题目让你计算上一个更大元素,或者计算上一个更大或相等的元素,应该如何修改对应的模板呢?而且在实际应用中,题目不会直接让你计算下一个(上一个)更大(小)的元素,你如何把问题转化成单调栈相关的问题呢?
我会在 单调栈的几种变体 对比单调栈的几种其他形式,并在 单调栈的运用 中给出单调栈的经典例题。更多数据结构设计类题目参见 数据结构设计经典习题。
引用本文的文章
引用本文的题目
安装 我的 Chrome 刷题插件 点开下列题目可直接查看解题思路:
_____________
《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复「全家桶」可下载配套 PDF 和刷题全家桶:

====其他语言代码====
java
ZakAnun 提供代码
// 496.下一个更大元素
// 暴力解法
public int[] nextGreaterElement(int[] nums1, int[] nums2) {
int[] result = new int[nums1.length];
for (int i = 0; i < nums1.length; i++) {
// 需要记录第一个数组每个元素在第二个数组中出现的位置
int index = 0;
for (int j = 0; j < nums2.length; j++) {
if (nums1[i] == nums2[j]) {
index = j;
break;
}
}
// 根据找到的位置往后遍历,若符合条件则记录到结果数组
for (int k = index; k < nums2.length; k++) {
if (nums2[k] > nums1[i]) {
result[i] = nums2[k];
break;
}
}
// 判断若对应位置结果依然为默认值,则将其修改为 -1
if (result[i] == 0) {
result[i] = -1;
}
}
return result;
}
// 分析: 暴力解法中需要确定数组1中每个元素在数组2中的下标而需要进行额外的遍历导致时间复杂度升高,
// 但若能够先罗列出全部的结果,然后从结果集中获取数组1中每个元素对应的下一个更大元素,就可以节省这部分时间(这里需要引用 HashMap 帮助我们记录结果,以便根据数组1获取。
// 单调栈解法
public int[] nextGreaterElement(int[] nums1, int[] nums2) {
Stack<Integer> stack = new Stack <>();
HashMap<Integer, Integer> map = new HashMap <>();
int[] result = new int[nums1.length];
for (int value : nums2) {
while (!stack.empty() && value > stack.peek()) {
map.put(stack.pop(), value);
}
stack.push(value);
}
while (!stack.empty()) {
map.put(stack.pop(), -1);
}
for (int i = 0; i < nums1.length; i++) {
result[i] = map.get(nums1[i]);
}
return result;
}ZakAnun 提供代码
// 739. Daily Temperatures
class Solution {
public int[] dailyTemperatures(int[] T) {
Stack<Integer> stack = new Stack<>();
int[] ans = new int[T.length];
for (int i = 0; i < T.length; i++) {
// 如果压栈之后不满足单调递减,弹出元素,直至保持单调性
while (!stack.isEmpty() && T[i] > T[stack.peek()]) {
int index = stack.pop();
// 被弹出的元素(T[index])都是小于当前的元素(T[i]),由于栈内元素单调递减,大于被弹出元素(index)的最近的就是当前元素(i)
ans[index] = i - index;
}
stack.push(i);
}
return ans;
}
}JiangangZhao提供【503.下一个更大元素II】【java】
class Solution {
public int[] nextGreaterElements(int[] nums) {
//数组长度
int n = nums.length;
//逻辑拼接,数组长度翻倍
int len = n*2 - 1;
//存储结果数组
int[] res = new int[n];
//存放索引,不是元素
LinkedList<Integer> s = new LinkedList<>();
//从前往后遍历
for (int i = 0; i < len; ++i) {
//索引要取模
int val = nums[i % n];
//当前元素比栈顶元素大,即是栈顶元素的下一个更大的元素
while (!s.isEmpty() && val > nums[s.peek()]) {
res[s.pop()] = val;
}
//i<n时入栈
if (i < n) {
s.push(i);
}
}
//栈中剩余的索引不存在下一个更大的元素,赋值-1
while (!s.isEmpty()) {
res[s.pop()] = -1;
}
return res;
}
}javascript
单调栈模板
这里需要用一个map记录nums2中各项的下一个更大值,为何?注意读题。
- nums1和nums2中所有整数 互不相同
- nums1 中的所有整数同样出现在 nums2 中
如果还是用数组的话,num1中元素在nums2中的位置并不好找,所以这里使用map来维护。
其它核心思想和上文中的大抵相同。值得注意的是,入栈顺序可以有正着入栈和倒着入栈,顺序不同,维护的动作也不同,详见下文。
正着入栈如下。
/**
* @param {number[]} nums1
* @param {number[]} nums2
* @return {number[]}
*/
var nextGreaterElement = function (nums1, nums2) {
let len1 = nums1.length;
let len2 = nums2.length;
// base case
if (len1 < 1 || len2 < 1 || len1 > len2) {
return [];
}
let res = new Array(len1); // 存放答案的数组
let stack = [];
let map = {};
// 启动条件
stack.push(nums2[0]);
// 右边数字入栈
for (let j = 1; j < len2; j++) {
let currNum = nums2[j];
// 单调栈栈顶元素和当前数组元素作比较
// 找到下一个更大元素
while (stack.length !== 0 && currNum > stack[stack.length - 1]) {
map[stack.pop()] = currNum;
}
stack.push(currNum);
}
// 栈不为空 这些元素都是找不到下一个更大值的
while (stack.length !== 0) {
map[stack.pop()] = -1;
}
for (let i = 0; i < len1; i++) {
res[i] = map[nums1[i]];
}
return res;
};接下来是倒着入栈,就是上文中提到的排队思路。
抽象思路,nums2看做排队找后面第一个比自己高的高个子。
var nextGreaterElement = function(nums1, nums2) {
// 把此类问题比作排队看后面第一个比自己高的
// 从后面开始遍历往前面看,就能很好的避免不知道后面什么情况了
let stack = []
let res = []
let map = new Map()
for(let i = nums2.length - 1; i >= 0; i--){
// 矮个子起开,要你也没用,反正看不见你
while(stack.length && nums2[i] >= stack[stack.length - 1]){
stack.pop()
}
//有比我个子高的吗?有就是你了,没有就是-1
map.set(nums2[i], stack.length ? stack[stack.length - 1] : -1)
stack.push(nums2[i])
}
nums1.forEach(item => {
res.push(map.get(item))
})
return res;
};
解决了这道题,后面的题就很容易理解了。在这道题的基础上,让单调栈中存放的元素是下标而不是值,因为有的题目需要根据下标计算,这样泛化性更好。
正着入栈,存储下标。
/**
* @param {number[]} nums1
* @param {number[]} nums2
* @return {number[]}
*/
var nextGreaterElement = function (nums1, nums2) {
let len1 = nums1.length;
let len2 = nums2.length;
// base case
if (len1 < 1 || len2 < 1 || len1 > len2) {
return [];
}
let map = new Map()
let res = []; // 存放结果
let stack = []
for (let i = 0; i < len2; i++) {
//栈顶元素存在,并且当前的元素大于栈顶
while (stack.length && nums2[i] > nums2[stack[stack.length - 1]]) {
// 关键步骤1
let index = stack.pop();
map.set(nums2[index], nums2[i])
}
// 关键步骤2 下标入栈
stack.push(i)
}
//栈内还有元素,说明后面没有比自己小的了
while (stack.length) {
let index = stack.pop();
map.set(nums2[index], -1)
}
// 最后导出结果
nums1.forEach(item => {
res.push(map.get(item))
})
return res
};倒着入栈,存储下标。
// 存储的是下标
var nextGreaterElement = function (nums1, nums2) {
// 把此类问题比作排队看后面第一个比自己高的
// 从后面开始遍历往前面看,就能很好的避免不知道后面什么情况了
let stack = []
let res = []
let map = new Map()
for (let i = nums2.length - 1; i >= 0; i--) {
// 矮个子起开,要你也没用,反正看不见你
while (stack.length && nums2[i] >= nums2[stack[stack.length - 1]]) {
stack.pop()
}
//有比我个子高的吗?有就是你了,没有就是-1
map.set(nums2[i], stack.length ? nums2[stack[stack.length - 1]] : -1)
// 关键步骤:存储的是下标
stack.push(i)
}
nums1.forEach(item => {
res.push(map.get(item))
})
return res;
};
进一步而谈,其实map也可以转化成使用index对应index,不过这种情况的题比较少见,了解即可,不必抛开框架深入追究细节。
nums1:[4,1,2]
nums2:[1,3,4,2]
直接num1的value对nums2的value (前提:value唯一)
{
4: -1
1: 3
2: -1
}
num1的index对nums2的index
这里也可以用数组来做,自由发挥吧,这里只提供一些思路。
{
0:-1,
1:1
2:-1
}因为是环形数组,所以最后一个数的下一个最大的数不是-1,而是要把再数组从头开始遍历到末尾得出这个数,可以把数组扩大两倍解决。
- 把数组扩大两倍逆序遍历依次放入栈中,栈中的栈顶元素代表下一个迭代的数的后面第一个最大的数;
- 当前数比栈顶元素大时,出栈;
- 此时栈有值时,栈顶元素即为当前数的下一个最大的数,把它存入结果数组对应的下标中;
- 把当前数入栈
这里用的和上文一样,还是反着入栈,相信读者可以自己悟出正着入栈怎么写了吧。
/**
* @param {number[]} nums
* @return {number[]}
*/
var nextGreaterElements = function (nums) {
let n = nums.length;
let res = [];
let stack = [];
// 假装这个数组长度翻倍了
for (let i = 2 * n - 1; i >= 0; i--) {
// 索引要求模,其他的和模板一样
while (stack.length && stack[stack.length - 1] <= nums[i % n])
stack.pop();
res[i % n] = stack.length ? stack[stack.length - 1] : -1;
stack.push(nums[i % n]);
}
return res;
};很简单,就是第一个next greater的变形而已,存储的是索引。
倒着入栈。
/**
* @param {number[]} T
* @return {number[]}
*/
var dailyTemperatures = function (T) {
let res = new Array(T.length).fill(0);
// 这里放元素索引,而不是元素
let stack = [];
/* 单调栈模板 */
for (let i = T.length - 1; i >= 0; i--) {
while (stack.length !== 0 && T[stack[stack.length - 1]] <= T[i]) {
stack.pop();
}
// 得到索引间距
res[i] = stack.length === 0 ? 0 : (stack[stack.length - 1] - i);
// 将索引入栈,而不是元素
stack.push(i);
}
return res;
};正着入栈,es6写法。
const dailyTemperatures = (T) => {
const res = new Array(T.length).fill(0);
for (let i = 0; i < T.length; i++) {
for (let j = i + 1; j < T.length; j++) {
if (T[j] > T[i]) {
res[i] = j - i;
break;
}
}
}
return res;
}部分做题规律如下,仅供做题套路参考,实际可以自由发挥。
当前项向左找第一个比自己大的位置:从左向右维护一个单调递减栈 当前项向左找第一个比自己小的位置:从左向右维护一个单调递增栈 当前项向右找第一个比自己大的位置:从右向左维护一个单调递减栈 当前项向右找第一个比自己小的位置:从右向左维护一个单调递增栈



