二叉堆详解实现优先级队列

通知:数据结构精品课 和 递归算法专题课 限时附赠网站会员,全新纸质书《labuladong 的算法笔记》 出版,签名版限时半价!另外,建议你在我的 网站 学习文章,体验更好。
-----------
二叉堆(Binary Heap)没什么神秘,性质比二叉搜索树 BST 还简单。其主要操作就两个,sink(下沉)和 swim(上浮),用以维护二叉堆的性质。其主要应用有两个,首先是一种排序方法「堆排序」,第二是一种很有用的数据结构「优先级队列」。
本文参考《算法 4》的代码,以实现优先级队列(Priority Queue)为例,来讲讲一下二叉堆怎么运作的。
一、二叉堆概览
首先,二叉堆和二叉树有啥关系呢,为什么人们总是把二叉堆画成一棵二叉树?
因为,二叉堆在逻辑上其实是一种特殊的二叉树(完全二叉树),只不过存储在数组里。一般的链表二叉树,我们操作节点的指针,而在数组里,我们把数组索引作为指针:
// 父节点的索引
int parent(int root) {
return root / 2;
}
// 左孩子的索引
int left(int root) {
return root * 2;
}
// 右孩子的索引
int right(int root) {
return root * 2 + 1;
}画个图你立即就能理解了,比如 arr 是一个字符数组,注意数组的第一个索引 0 空着不用:
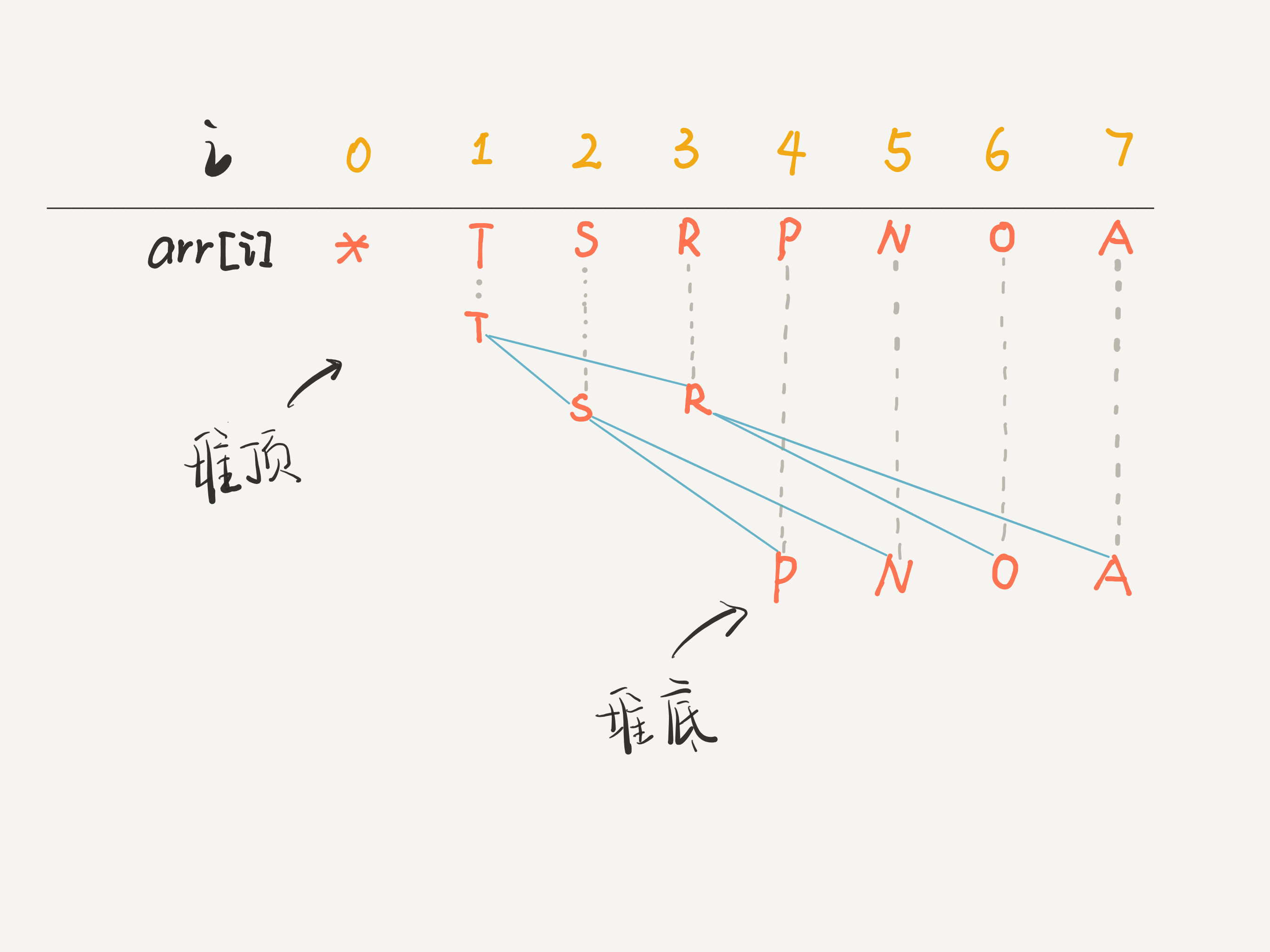
你看到了,因为这棵二叉树是「完全二叉树」,所以把 arr[1] 作为整棵树的根的话,每个节点的父节点和左右孩子的索引都可以通过简单的运算得到,这就是二叉堆设计的一个巧妙之处。
为了方便讲解,下面都会画的图都是二叉树结构,相信你能把树和数组对应起来。
二叉堆还分为最大堆和最小堆。最大堆的性质是:每个节点都大于等于它的两个子节点。类似的,最小堆的性质是:每个节点都小于等于它的子节点。
两种堆核心思路都是一样的,本文以最大堆为例讲解。
对于一个最大堆,根据其性质,显然堆顶,也就是 arr[1] 一定是所有元素中最大的元素。
二、优先级队列概览
优先级队列这种数据结构有一个很有用的功能,你插入或者删除元素的时候,元素会自动排序,这底层的原理就是二叉堆的操作。
数据结构的功能无非增删查改,优先级队列有两个主要 API,分别是 insert 插入一个元素和 delMax 删除最大元素(如果底层用最小堆,那么就是 delMin)。
下面我们实现一个简化的优先级队列,先看下代码框架:
tip:这里用到 Java 的泛型,
Key可以是任何一种可比较大小的数据类型,比如 Integer 等类型。
public class MaxPQ
<Key extends Comparable<Key>> {
// 存储元素的数组
private Key[] pq;
// 当前 Priority Queue 中的元素个数
private int size = 0;
public MaxPQ(int cap) {
// 索引 0 不用,所以多分配一个空间
pq = (Key[]) new Comparable[cap + 1];
}
/* 返回当前队列中最大元素 */
public Key max() {
return pq[1];
}
/* 插入元素 e */
public void insert(Key e) {...}
/* 删除并返回当前队列中最大元素 */
public Key delMax() {...}
/* 上浮第 x 个元素,以维护最大堆性质 */
private void swim(int x) {...}
/* 下沉第 x 个元素,以维护最大堆性质 */
private void sink(int x) {...}
/* 交换数组的两个元素 */
private void swap(int i, int j) {
Key temp = pq[i];
pq[i] = pq[j];
pq[j] = temp;
}
/* pq[i] 是否比 pq[j] 小? */
private boolean less(int i, int j) {
return pq[i].compareTo(pq[j]) < 0;
}
/* 还有 left, right, parent 三个方法 */
}空出来的四个方法是二叉堆和优先级队列的奥妙所在,下面用图文来逐个理解。
三、实现 swim 和 sink
为什么要有上浮 swim 和下沉 sink 的操作呢?为了维护堆结构。
我们要讲的是最大堆,每个节点都比它的两个子节点大,但是在插入元素和删除元素时,难免破坏堆的性质,这就需要通过这两个操作来恢复堆的性质了。
对于最大堆,会破坏堆性质的有两种情况:
1、如果某个节点 A 比它的子节点(中的一个)小,那么 A 就不配做父节点,应该下去,下面那个更大的节点上来做父节点,这就是对 A 进行下沉。
2、如果某个节点 A 比它的父节点大,那么 A 不应该做子节点,应该把父节点换下来,自己去做父节点,这就是对 A 的上浮。
当然,错位的节点 A 可能要上浮(或下沉)很多次,才能到达正确的位置,恢复堆的性质。所以代码中肯定有一个 while 循环。
细心的读者也许会问,这两个操作不是互逆吗,所以上浮的操作一定能用下沉来完成,为什么我还要费劲写两个方法?
是的,操作是互逆等价的,但是最终我们的操作只会在堆底和堆顶进行(等会讲原因),显然堆底的「错位」元素需要上浮,堆顶的「错位」元素需要下沉。
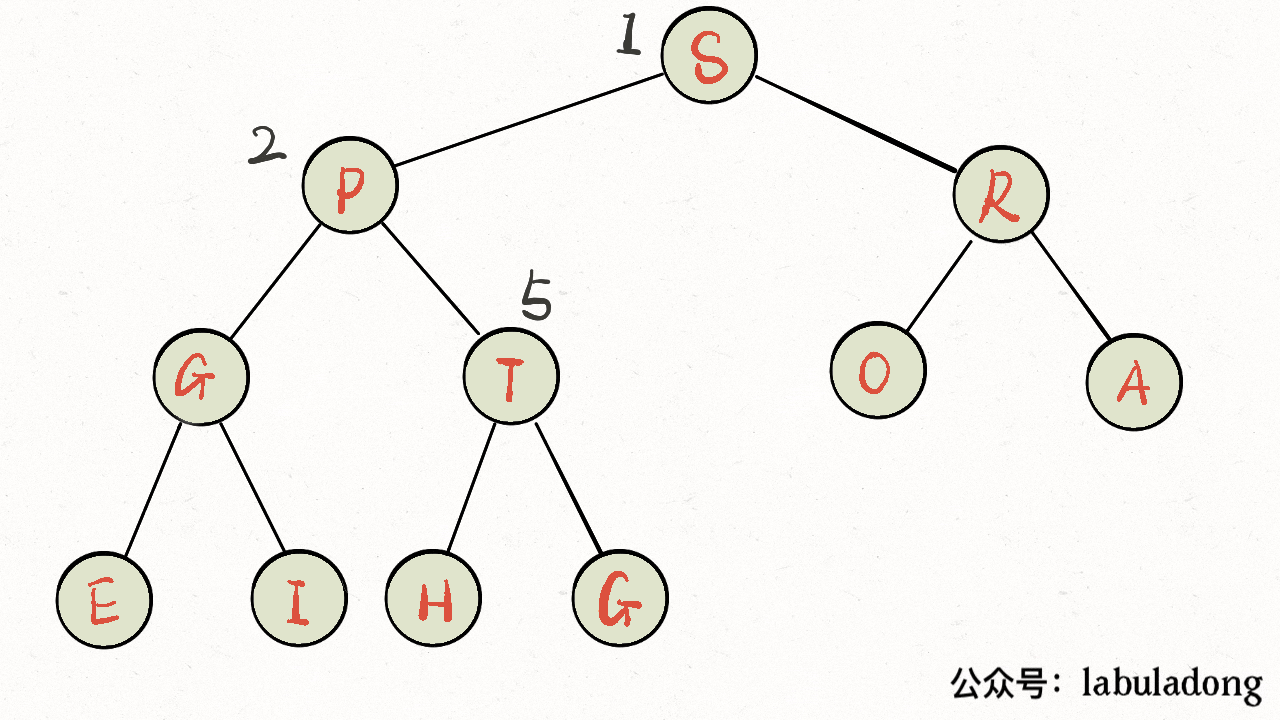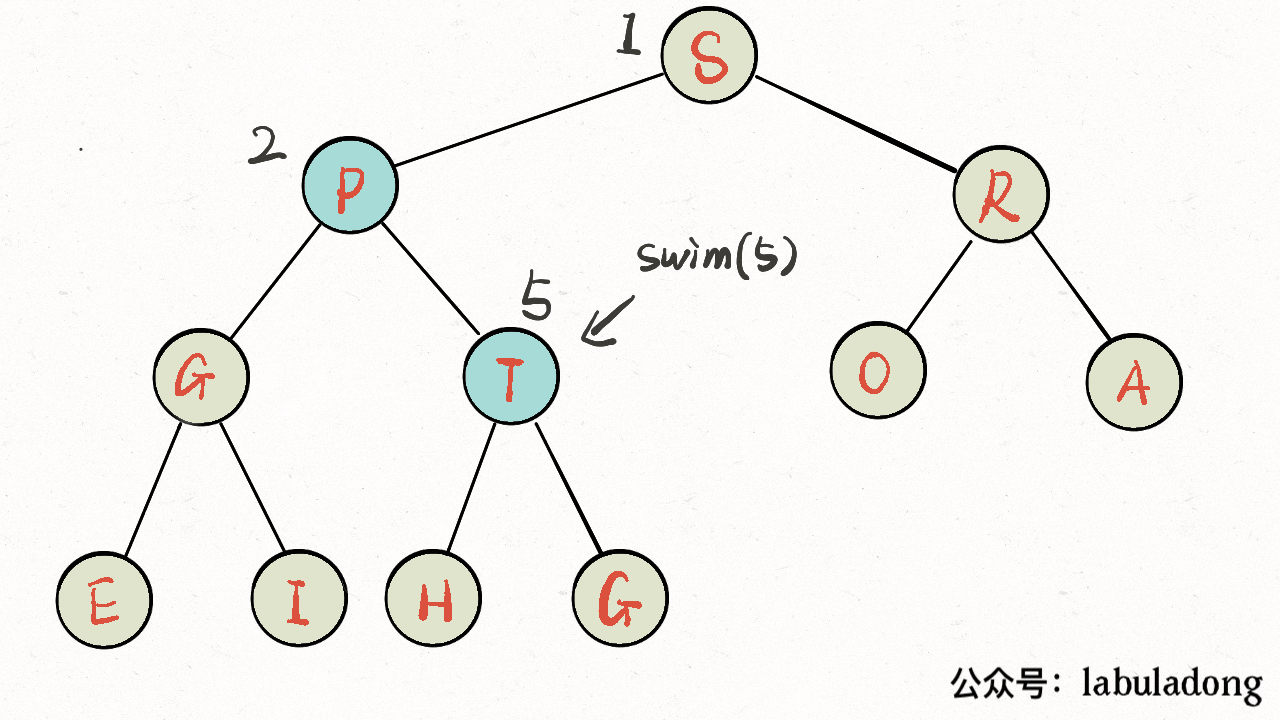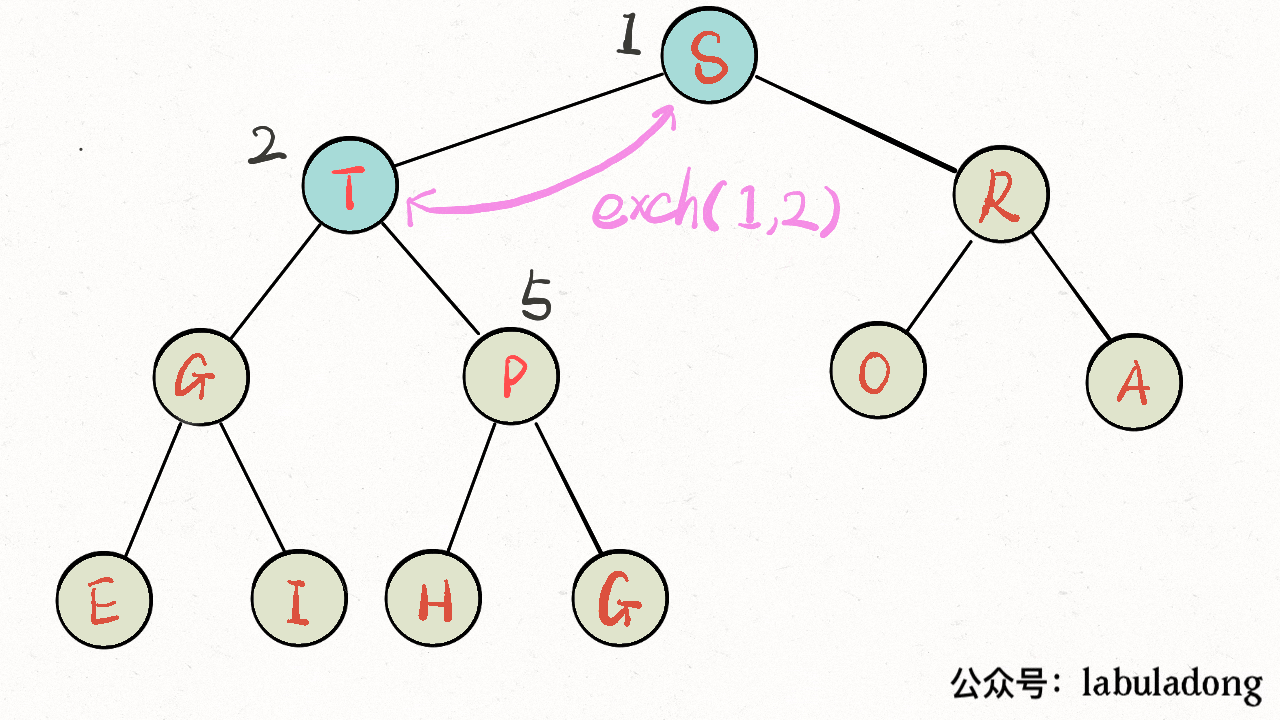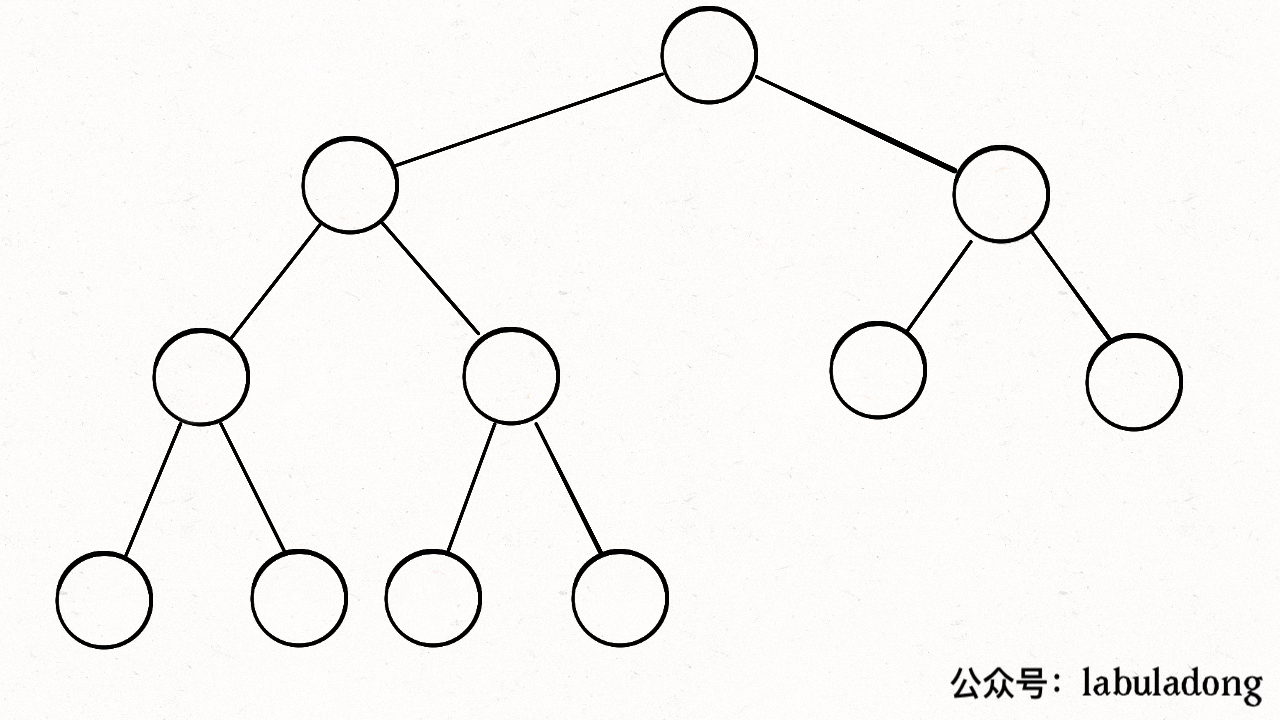
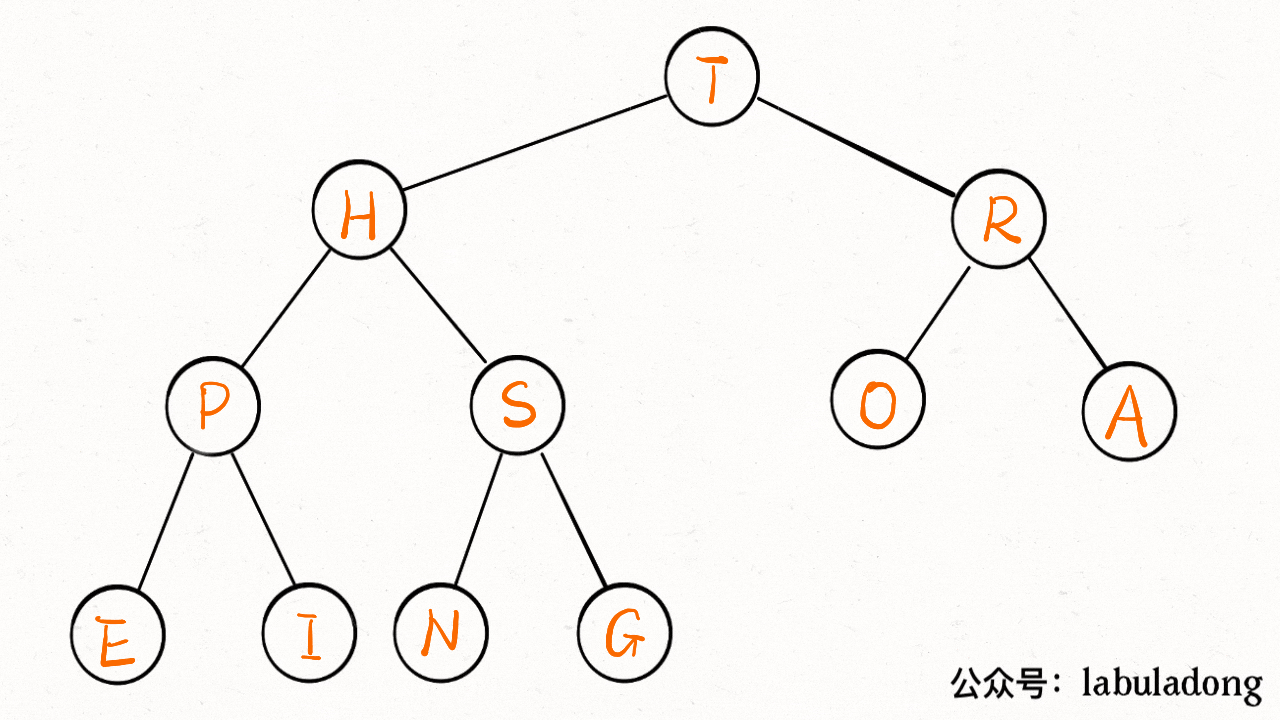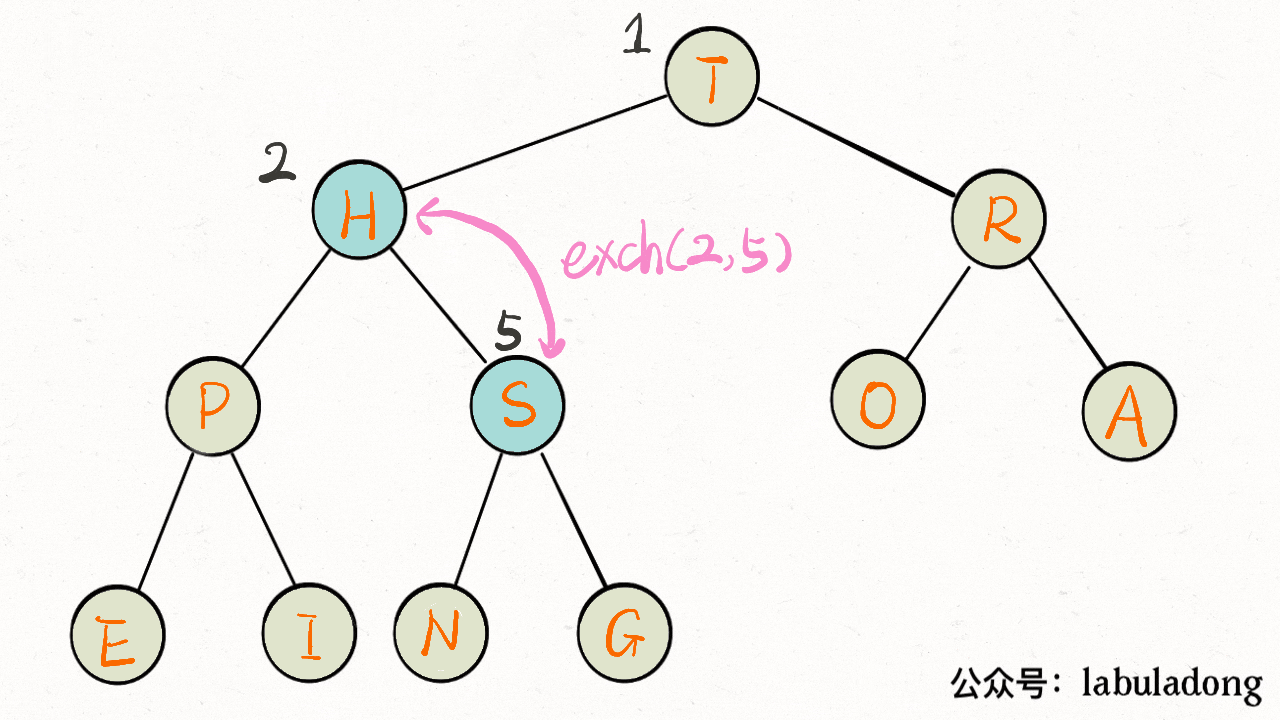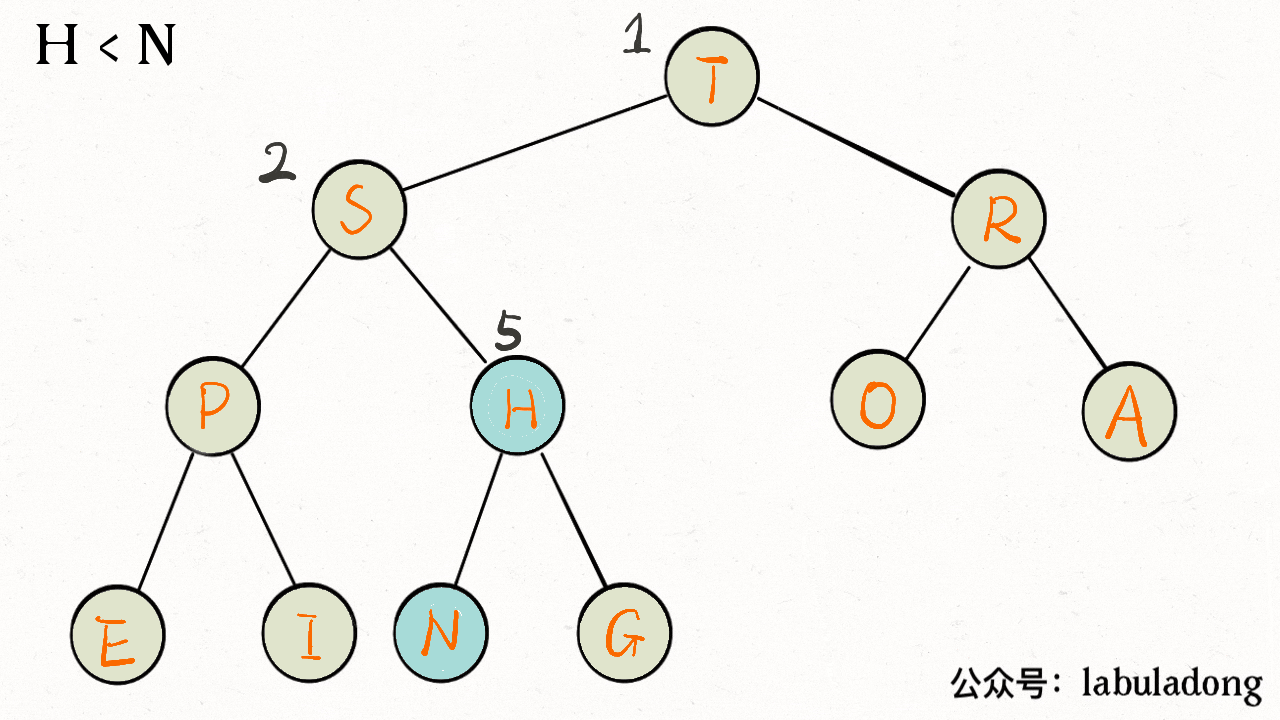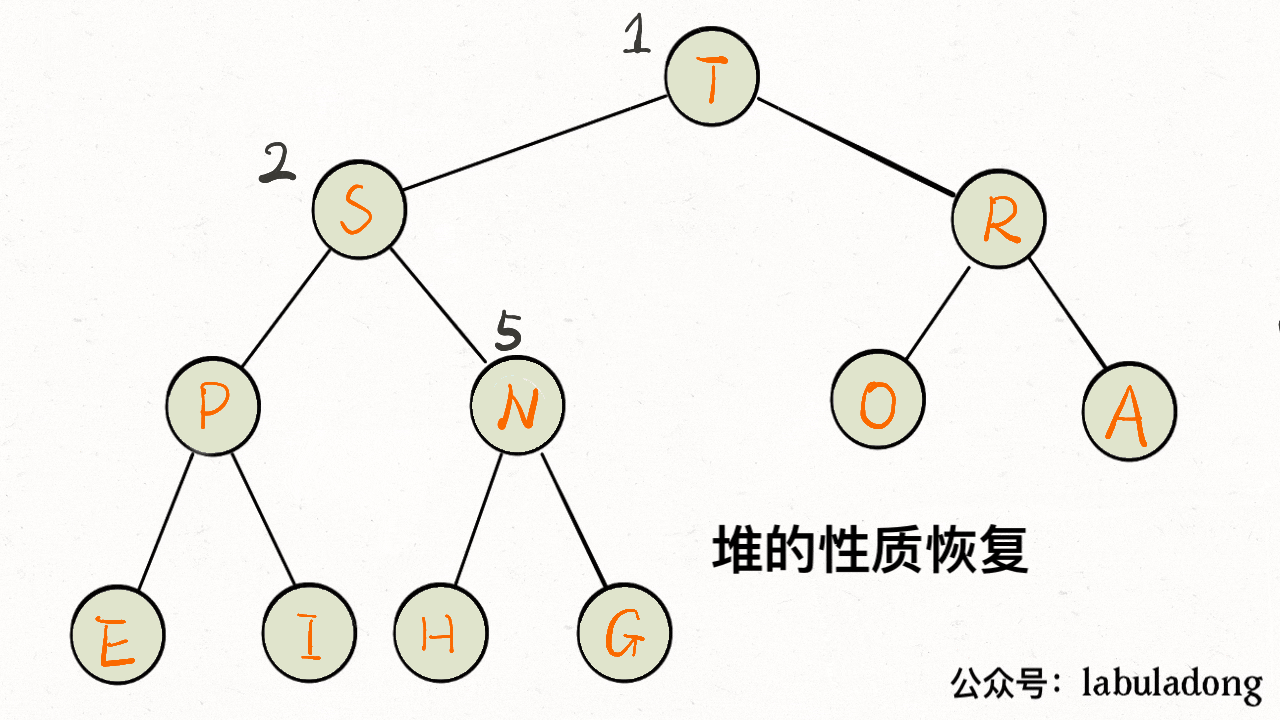
上浮的代码实现:
public class MaxPQ <Key extends Comparable<Key>> {
// 为了节约篇幅,省略上文给出的代码部分...
private void swim(int x) {
// 如果浮到堆顶,就不能再上浮了
while (x > 1 && less(parent(x), x)) {
// 如果第 x 个元素比上层大
// 将 x 换上去
swap(parent(x), x);
x = parent(x);
}
}
}画个 GIF 看一眼就明白了:
下沉的代码实现:
下沉比上浮略微复杂一点,因为上浮某个节点 A,只需要 A 和其父节点比较大小即可;但是下沉某个节点 A,需要 A 和其两个子节点比较大小,如果 A 不是最大的就需要调整位置,要把较大的那个子节点和 A 交换。
public class MaxPQ <Key extends Comparable<Key>> {
// 为了节约篇幅,省略上文给出的代码部分...
private void sink(int x) {
// 如果沉到堆底,就沉不下去了
while (left(x) <= size) {
// 先假设左边节点较大
int max = left(x);
// 如果右边节点存在,比一下大小
if (right(x) <= size && less(max, right(x)))
max = right(x);
// 结点 x 比俩孩子都大,就不必下沉了
if (less(max, x)) break;
// 否则,不符合最大堆的结构,下沉 x 结点
swap(x, max);
x = max;
}
}
}画个 GIF 看下就明白了:
至此,二叉堆的主要操作就讲完了,一点都不难吧,代码加起来也就十行。明白了 sink 和 swim 的行为,下面就可以实现优先级队列了。
四、实现 delMax 和 insert
这两个方法就是建立在 swim 和 sink 上的。
insert 方法先把要插入的元素添加到堆底的最后,然后让其上浮到正确位置。
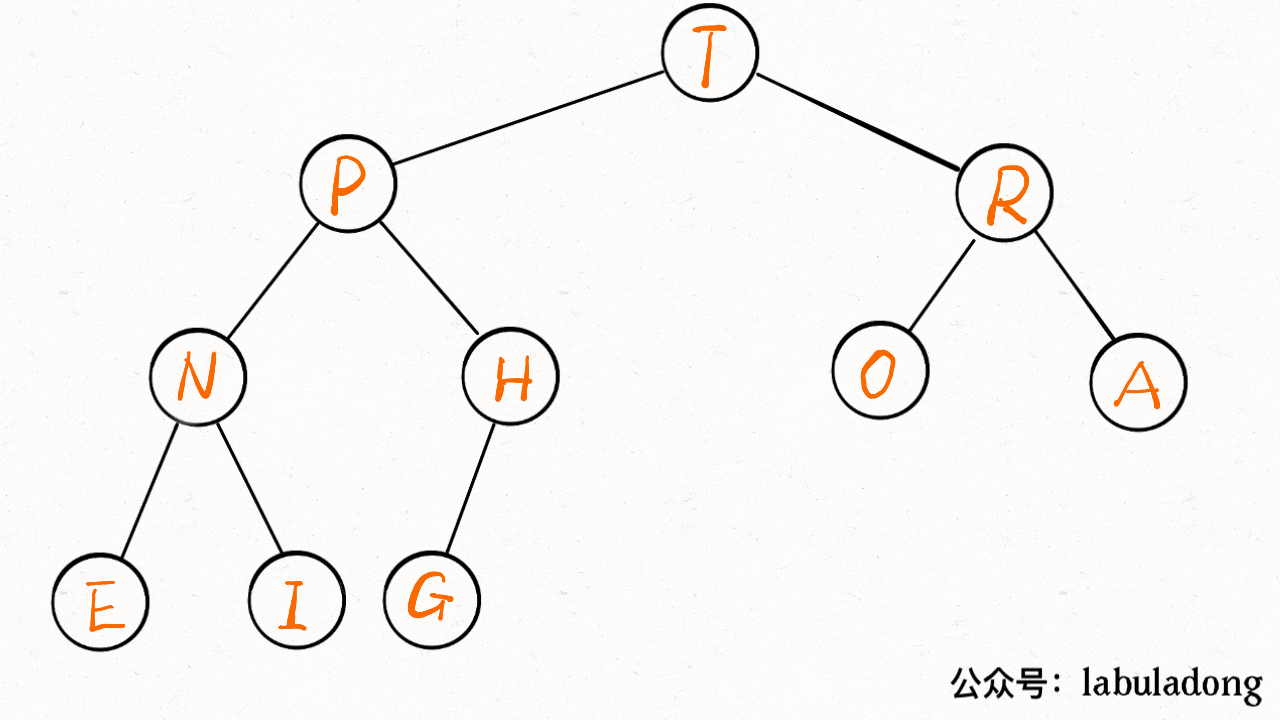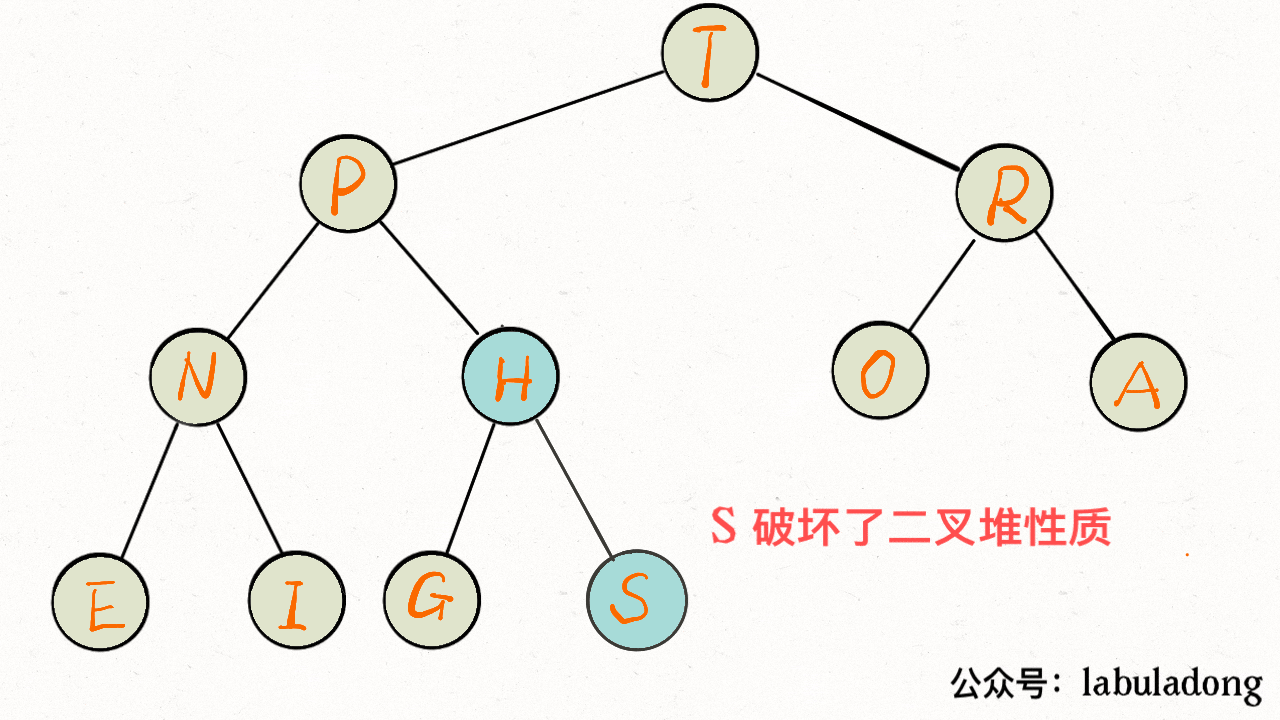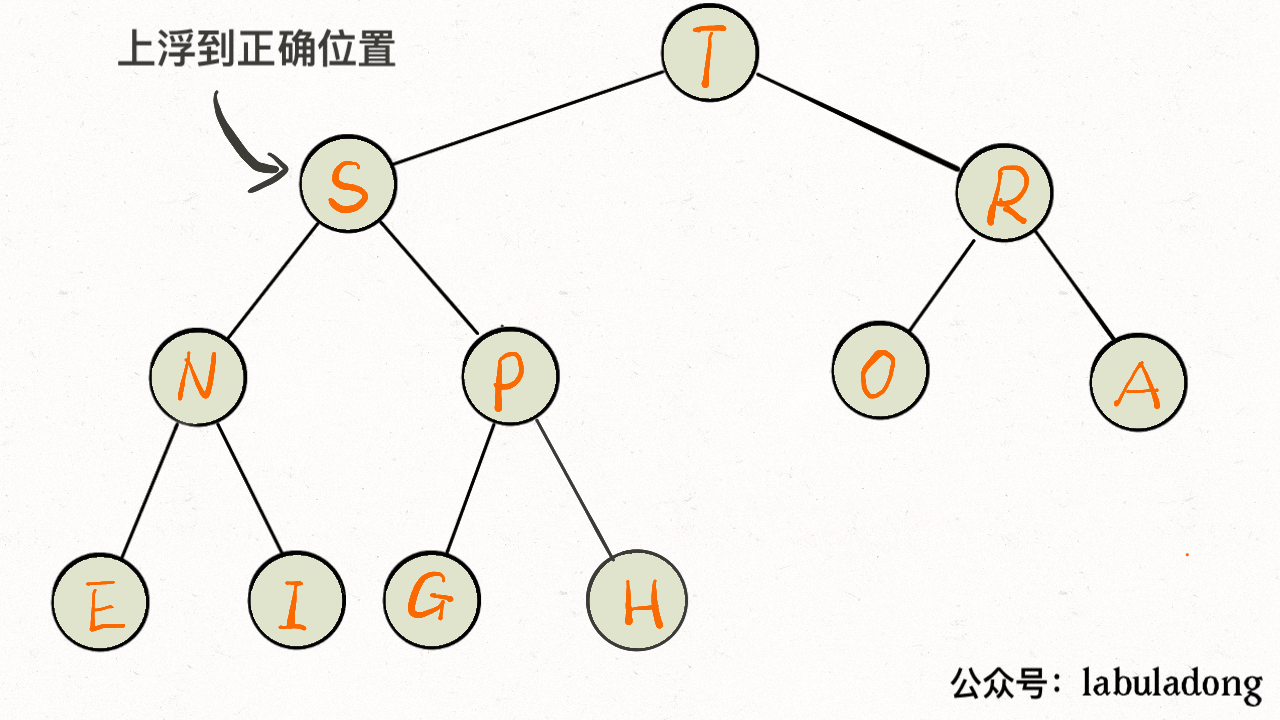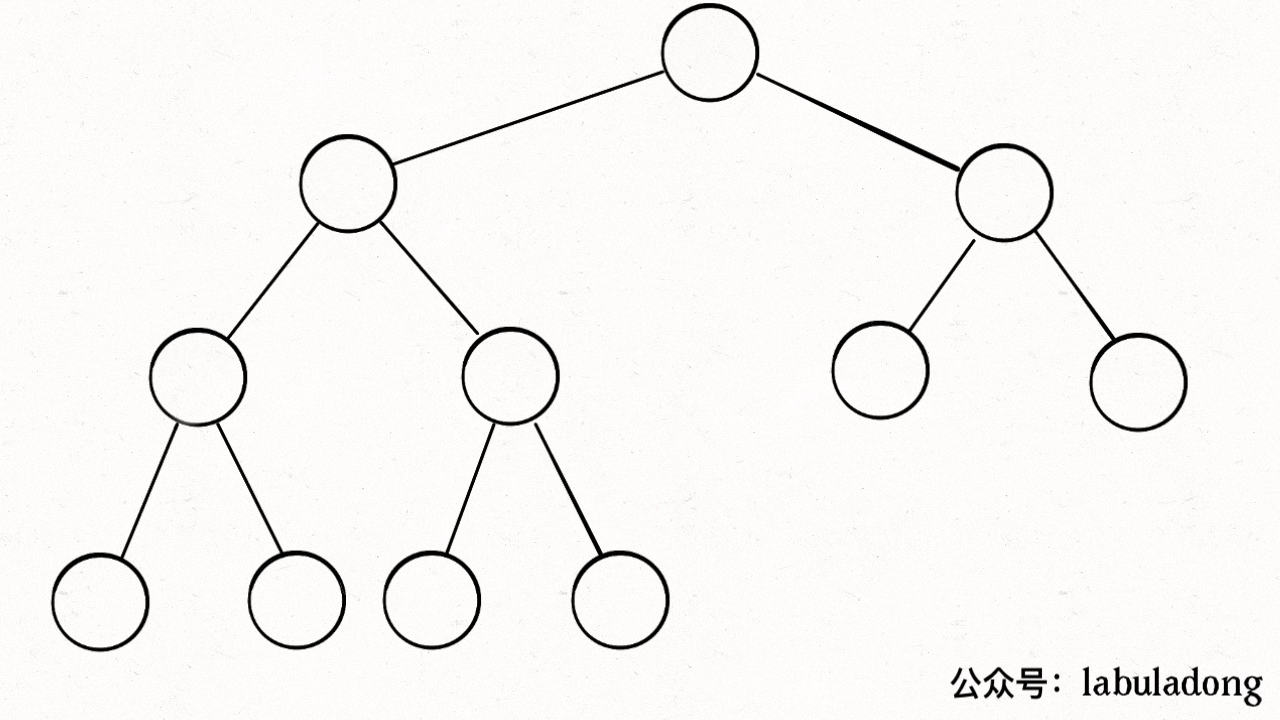
public class MaxPQ <Key extends Comparable<Key>> {
// 为了节约篇幅,省略上文给出的代码部分...
public void insert(Key e) {
size++;
// 先把新元素加到最后
pq[size] = e;
// 然后让它上浮到正确的位置
swim(size);
}
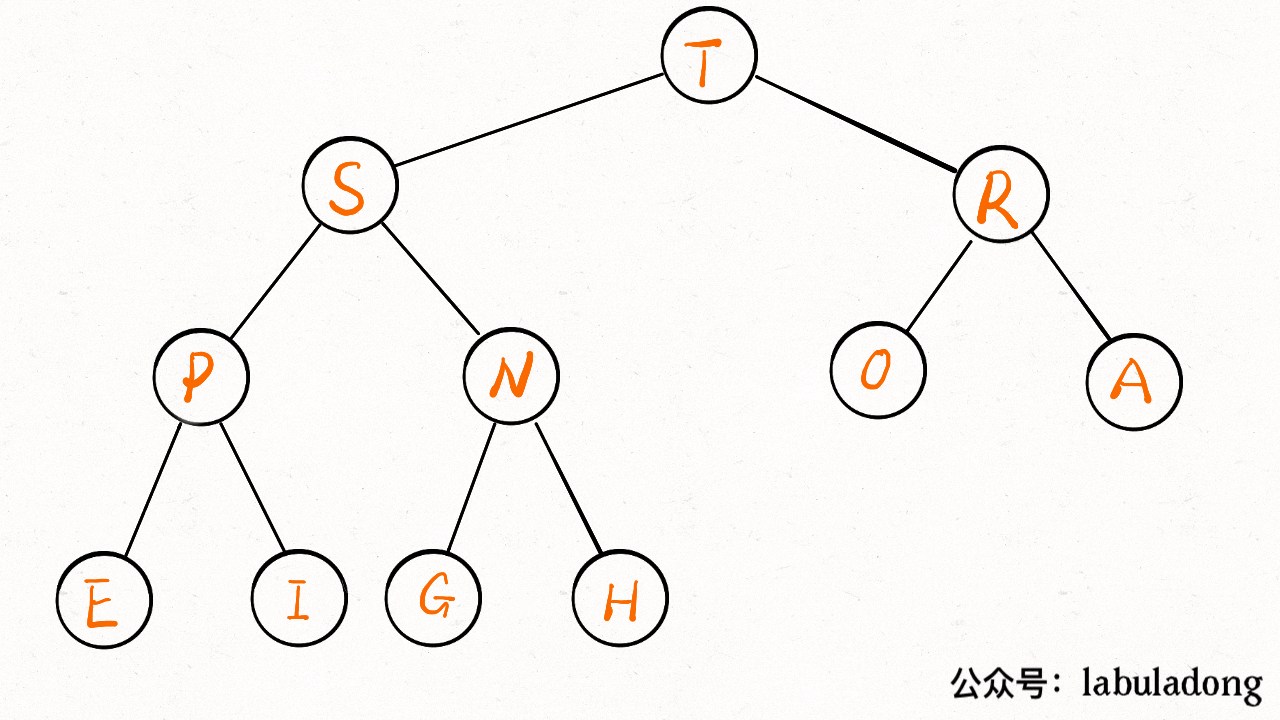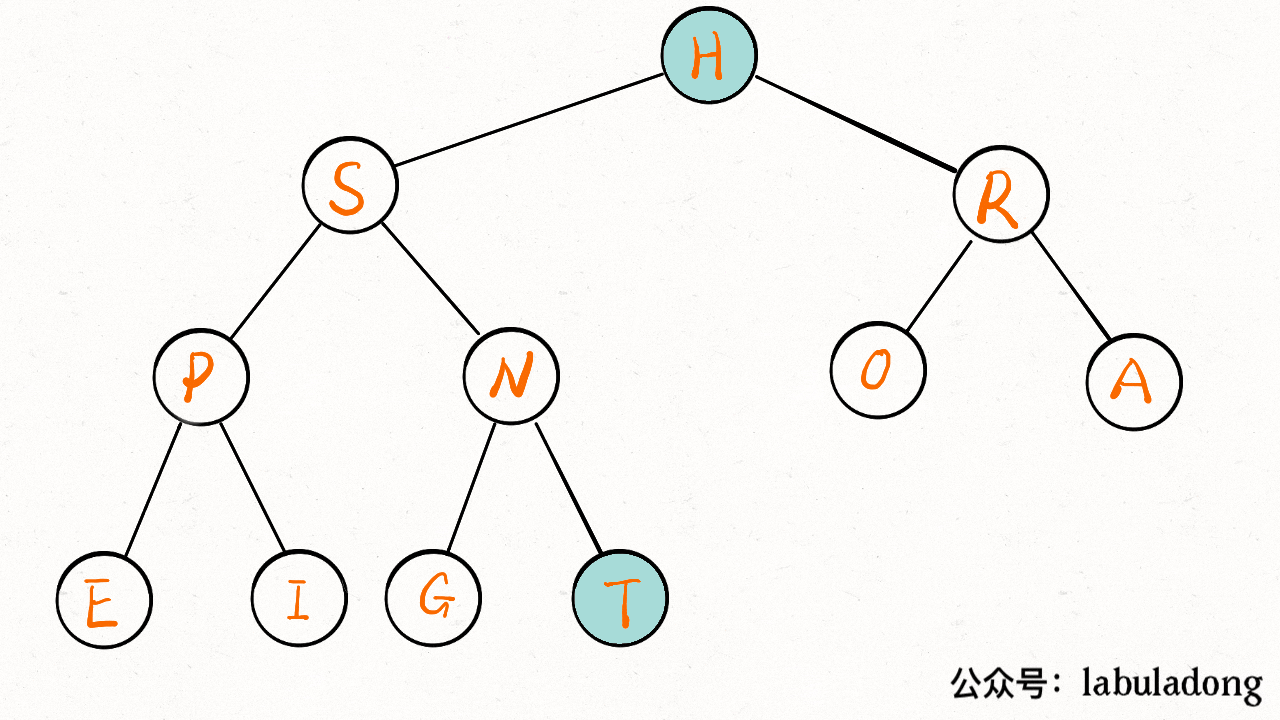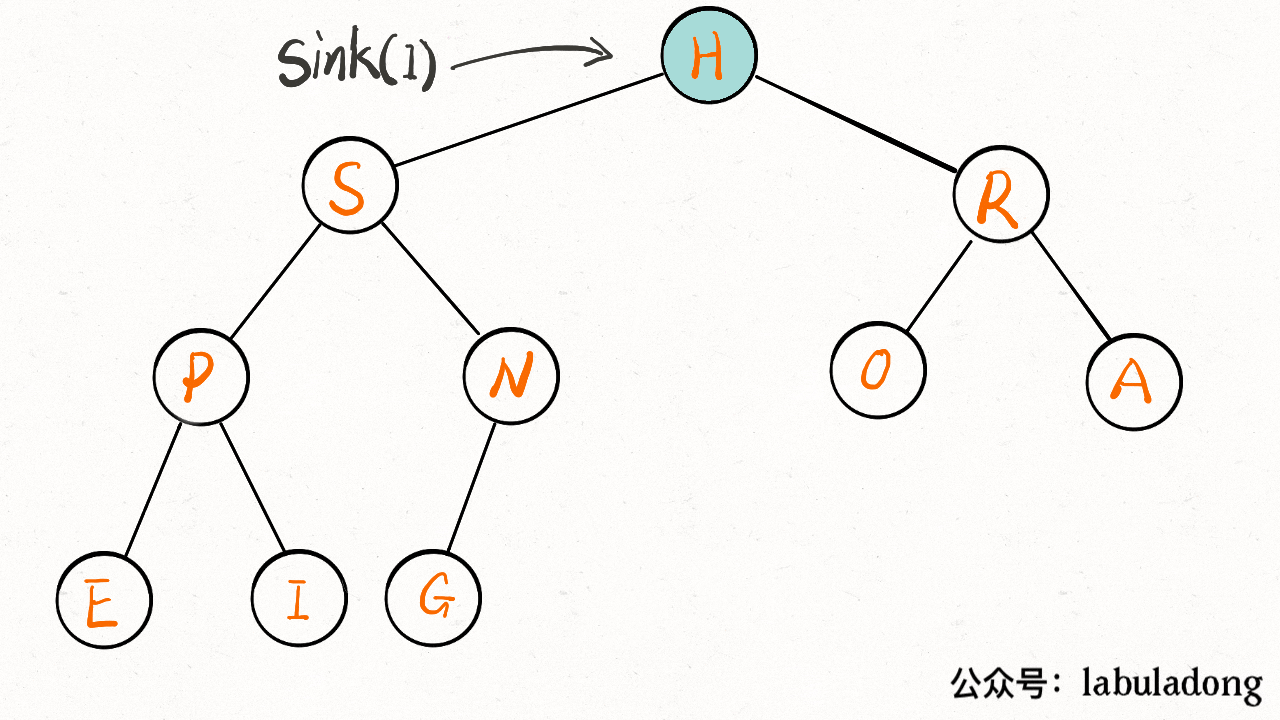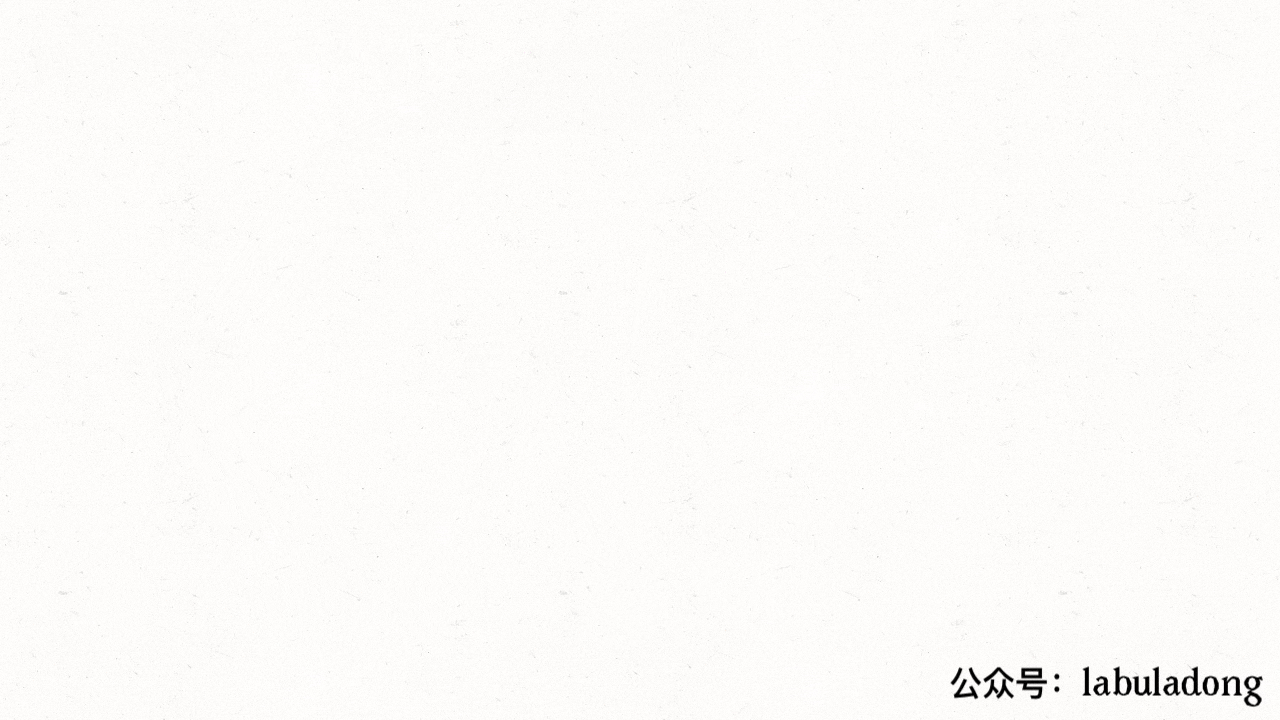
}delMax 方法先把堆顶元素 A 和堆底最后的元素 B 对调,然后删除 A,最后让 B 下沉到正确位置。
public class MaxPQ <Key extends Comparable<Key>> {
// 为了节约篇幅,省略上文给出的代码部分...
public Key delMax() {
// 最大堆的堆顶就是最大元素
Key max = pq[1];
// 把这个最大元素换到最后,删除之
swap(1, size);
pq[size] = null;
size--;
// 让 pq[1] 下沉到正确位置
sink(1);
return max;
}
}
至此,一个优先级队列就实现了,插入和删除元素的时间复杂度为 O(logK),K 为当前二叉堆(优先级队列)中的元素总数。因为我们时间复杂度主要花费在 sink 或者 swim 上,而不管上浮还是下沉,最多也就树(堆)的高度,也就是 log 级别。
五、最后总结
二叉堆就是一种完全二叉树,所以适合存储在数组中,而且二叉堆拥有一些特殊性质。
二叉堆的操作很简单,主要就是上浮和下沉,来维护堆的性质(堆有序),核心代码也就十行。
优先级队列是基于二叉堆实现的,主要操作是插入和删除。插入是先插到最后,然后上浮到正确位置;删除是调换位置后再删除,然后下沉到正确位置。核心代码也就十行。
也许这就是数据结构的威力,简单的操作就能实现巧妙的功能,真心佩服发明二叉堆算法的人!
最后,更多二叉堆/优先级队列相关的题目练习见 二叉堆(优先级队列)的经典习题。
引用本文的题目
安装 我的 Chrome 刷题插件 点开下列题目可直接查看解题思路:
_____________
《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复「全家桶」可下载配套 PDF 和刷题全家桶:

====其他语言代码====
javascript
/**
* 最大堆
*/
function left(i) {
return i * 2 + 1;
}
function right(i) {
return i * 2 + 2;
}
function swap(A, i, j) {
const t = A[i];
A[i] = A[j];
A[j] = t;
}
class Heap {
constructor(arr) {
this.data = [...arr];
this.size = this.data.length;
}
/**
* 重构堆
*/
rebuildHeap() {
const L = Math.floor(this.size / 2);
for (let i = L - 1; i >= 0; i--) {
this.maxHeapify(i);
}
}
isHeap() {
const L = Math.floor(this.size / 2);
for (let i = L - 1; i >= 0; i++) {
const l = this.data[left(i)] || Number.MIN_SAFE_INTEGER;
const r = this.data[right(i)] || Number.MIN_SAFE_INTEGER;
const max = Math.max(this.data[i], l, r);
if (max !== this.data[i]) {
return false;
}
return true;
}
}
sort() {
for (let i = this.size - 1; i > 0; i--) {
swap(this.data, 0, i);
this.size--;
this.maxHeapify(0);
}
}
insert(key) {
this.data[this.size++] = key;
if (this.isHeap()) {
return;
}
this.rebuildHeap();
}
delete(index) {
if (index >= this.size) {
return;
}
this.data.splice(index, 1);
this.size--;
if (this.isHeap()) {
return;
}
this.rebuildHeap();
}
/**
* 堆的其他地方都满足性质
* 唯独跟节点,重构堆性质
* @param {*} i
*/
maxHeapify(i) {
let max = i;
if (i >= this.size) {
return;
}
// 求左右节点中较大的序号
const l = left(i);
const r = right(i);
if (l < this.size && this.data[l] > this.data[max]) {
max = l;
}
if (r < this.size && this.data[r] > this.data[max]) {
max = r;
}
// 如果当前节点最大,已经是最大堆
if (max === i) {
return;
}
swap(this.data, i, max);
// 递归向下继续执行
return this.maxHeapify(max);
}
}
module.exports = Heap;


